문제
문제 설명
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
- 다음 칸은 경계선이다.
- (x, y), (x+1, y-1), ..., (x+d1, y-d1)
- (x, y), (x+1, y+1), ..., (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
- 경계선과 경계선의 안에 포함되어있는 곳은 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.
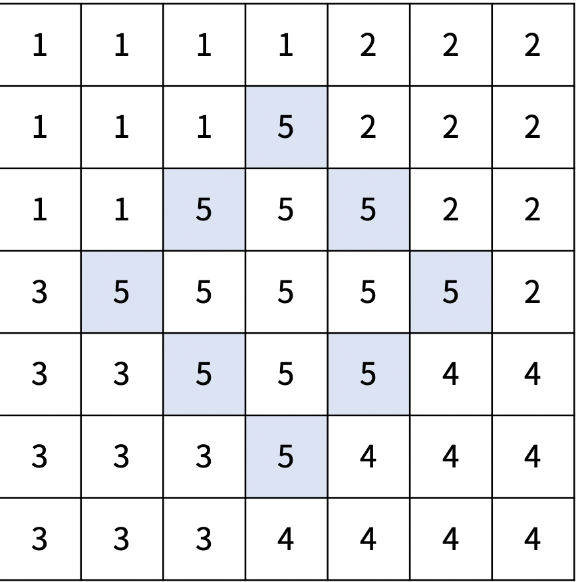 | 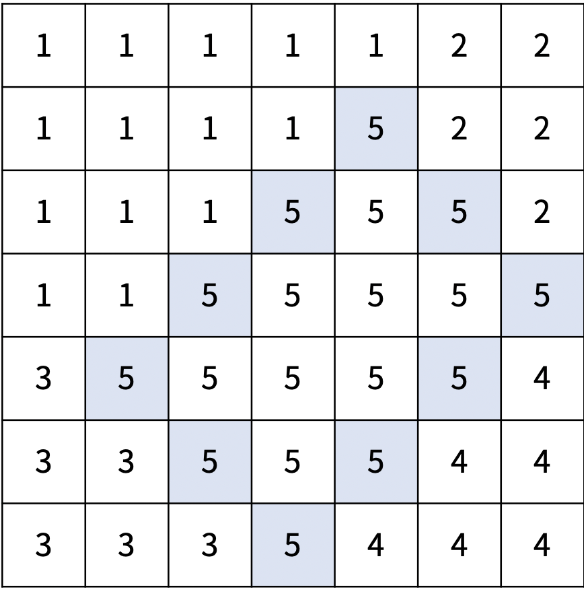 | 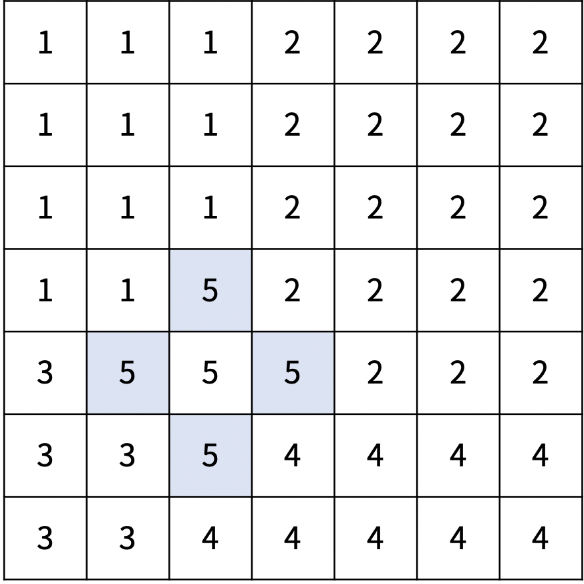 |
|---|---|---|
| x = 2, y = 4, d1 = 2, d2 = 2 | x = 2, y = 5, d1 = 3, d2 = 2 | x = 4, y = 3, d1 = 1, d2 = 1 |
구역 (r, c)의 인구는 A(r)(c)이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
입력 조건
첫째 줄에 재현시의 크기 N이 주어진다.
둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A(r)(c)를 의미한다.
출력 조건
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.
제한 사항
- 5 ≤ N ≤ 20
- 1 ≤ A(r)(c) ≤ 100
정답 및 풀이
정답 코드
import sys
from collections import defaultdict
n = int(sys.stdin.readline().rstrip())
g = [list(map(int, sys.stdin.readline().rstrip().split())) for _ in range(n)]
election = [[]]
ans = sys.maxsize
def divide_area(a, b, e1, e2):
global election
election = [[0 for _ in range(n + 1)] for __ in range(n + 1)]
for r in range(1, b + e1):
for c in range(1, a + 1):
election[r][c] = 1
for r in range(1, b + e2 + 1):
for c in range(a + 1, n + 1):
election[r][c] = 2
for r in range(b + e1, n + 1):
for c in range(1, a - e1 + e2):
election[r][c] = 3
for r in range(b + e2 + 1, n + 1):
for c in range(a - e1 + e2, n + 1):
election[r][c] = 4
for i in range(e1 + 1):
election[b + i][a - i] = 5
for i in range(e2 + 1):
election[b + i][a + i] = 5
for i in range(e2 + 1):
election[b + e1 + i][a - e1 + i] = 5
for i in range(e1 + 1):
election[b + e2 + i][a + e2 - i] = 5
for i in range(b + 1, b + e1 + e2):
is_five = False
for j in range(1, n + 1):
if election[i][j] == 5:
is_five = not is_five
else:
if is_five:
election[i][j] = 5
def calculate_population():
global ans
d = defaultdict(int)
for a in range(1, n + 1):
for b in range(1, n + 1):
d[election[a][b]] += g[a - 1][b - 1]
ans = min(max(d.values()) - min(d.values()), ans)
def in_range(a, b, e1, e2):
if a - e1 <= 0 or a + e1 > n + 1:
return False
if b + e1 + e1 > n + 1:
return False
return True
for x in range(1, n + 1):
for y in range(1, n + 1):
for d1 in range(1, x):
for d2 in range(1, n - x + 1):
if d1 + d2 <= n - y and in_range(x, y, d1, d2):
divide_area(x, y, d1, d2)
calculate_population()
print(ans)
풀이
제 기준으로는 정말정말 어렵게 풀었던 문제입니다ㅠㅠㅠ
1. 그냥 브루트포스로 푸는 삼성 문제
2. 골드 3이라는 난이도
요 2개만 보고 풀다가... 좌표가 이상해서 제 방식대로 고치면서 푸느라 2시간이 넘게 걸려서 겨우겨우 풀었습니다 ㅠㅠㅠ
난이도 자체는 그렇게 높지는 않아 보이는데... 제 구현 능력이 부족해서 많이 고생했던 문제입니다.
저는
for i in range(n):
for j in range(n):
g[i][j] ...이런 식으로 문제를 풀기 때문에 i에 y 좌표를 넣고, j에 x좌표를 넣는 방식으로 푸는데
여기서는 구역 (r, c)의 인구는 A(r)(c)라는 말과 같이 r => i => y, c => j => x 이런식으로 풀려고 했는데
r, c의 조건이 1 ≤ r < x+d1, 1 ≤ c ≤ y와 같이 제 기준과는 맞지 않아서.... 꽤 고생했습니다.
이거 때문에 너무 헷갈려서 시간이 너무 오래 걸렸어요ㅠㅠㅠ
그래서 어떻게 해결했느냐?
문제의 x는 내 기준의 y로 생각하고, 문제의 y는 내 기준의 x로 생각하기로 했습니다.
즉, 저는 문제의 모든 x,y를 y,x 로 치환해서 생각하면서 풀었습니다.
위의 제 풀이 조건을 인지하고 해설을 보시면 이해하기가 조금은 수월(?) 할겁니다...!!(아마두?)
그리고... 문제에서는 좌표를 다루는 방식이 제가 평소에 생각하는 방식(좌상단부터 우하단으로 오는 방식)과는 매우 상이 한 것 같아서 제 방식대로 커스텀을 마구마구해서 풀었습니다!!!
예를 들면 경계선을 긋는 방식을 제 방싱대로 풀어서 좌표는 밑의 그림과 같이 다르게 풀엇습니다

def divide_area :
문제의 조건에 따라 선거구를 구분하는 함수입니다.
1, 2, 3, 4번 선거구는 문제의 선거구를 나누는 기준 4번에 의거해서 번호를 구분합니다.
5번 선거구의 경우 경계선을 기준으로 내부의 구역을 표시해줘야 하기 때문에
1. 경계선을 우선 표시하고
2. 경계선 내부를 5번 선거구로 지정하는
방식으로 선거구를 지정했습니다.
각 인자는 다음과 같습니다
a: 경계선 표시 시작 x 좌표b: 경계선 표시 시작 y 좌표e1: 경계선 길이 1 즉 d1e2: 경계선 길이 2 즉 d2
def calculate_population()
이제 선거구를 구분했으니 각 선거구의 인구를 구해야겠죠
각 선거구별로 총 인구수를 각 구하는 함수입니다.
귀찮아서 defaultdict를 사용했습니다.
또 election 배열은 (n + 1) x (n + 1)로 선언했으므로 x, y 좌표를 g에 넣어줄 때 주의해서 넣어야합니다!
그리고 각 선거구 중 최고 인구수(max(d.values()))와 최저 인구수(min(d.values()))의 차를 구한다음,
ans와 비교해서 답을 갱신시켜 줍니다!
def in_range()
경계선을 그을 때 좌표 바깥으로 나가면 안되므로 해당 사항을 점검하는 함수입니다.
이 함수를 포함해서 x, y, d1, d2의 범위를 생각하는데 머리가 아팠습니다.
처음에는 막막했지만, 문제에 다행히 나와있더군요!
1. 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)여기서 가져왔습니다!!
우선 x와 y는 각각 1 ~ n까지 돌려줍니다.
그 다음 d1 과d2은 위의 조건을 활용합니다.
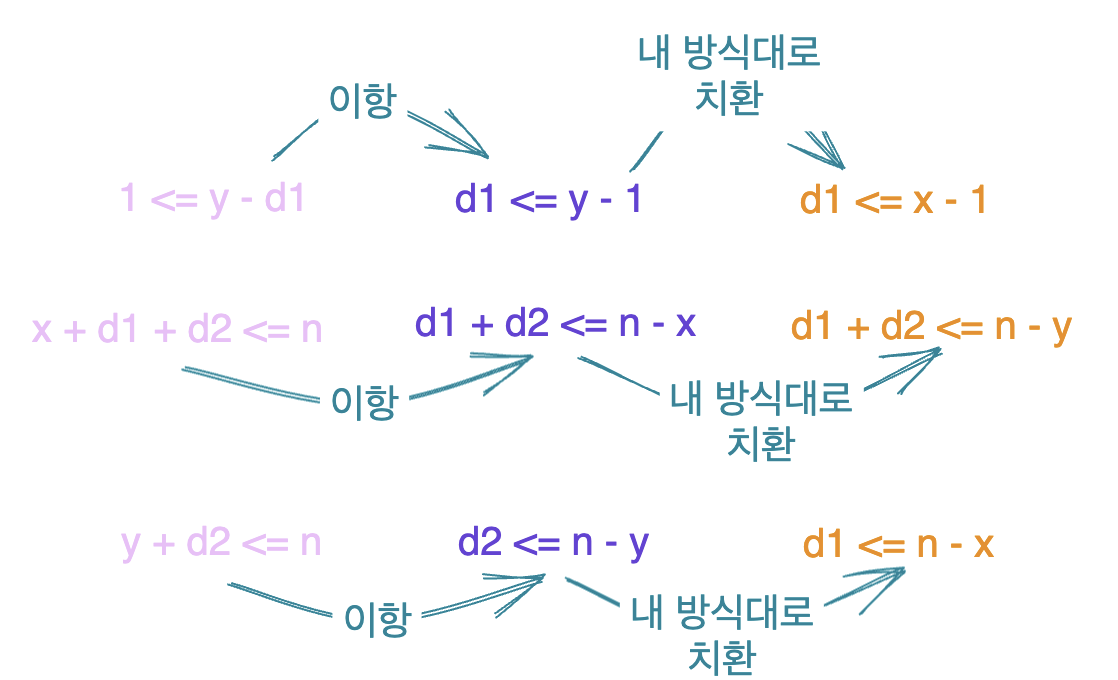
그래서 d1과 d2는 각각 다음과 같은 범위로 for문을 돌렸습니다!
for d1 in range(1, x):
for d2 in range(1, n - x + 1):그리고 다음 조건도 추가되었죠!
if d1 + d2 <= n - y:
...하지만 이렇게 돌리게 되니 범위를 벗어나는 몇몇 아이들이 생겼습니다.
그래서 조건을 더 강화했습니다.
(x, y) 를 기준으로
- x 좌표는 x - d1 이 1보다 작으면 안된다
- x 좌표는 x + d2가 n 보다 크면 안된다
- y 좌표는 y + d1 + d2가 n보다 크면 안된다.
이렇게 조건이 나옵니다
생각해보면 간단하죠 경계선을 다음과 같이 그으니까요!

제멋대로 생각하고 풀었기 때문에 문제의 좌표와는 상이합니다!!!!
기준점을 제외하고 나머지 3개 점만 살펴보면 되므로 살펴보면 되는 조건은 위 셋과 같고
in_range의 조건이 위의 정답 코드와 같이 나오게 됩니다!!
소감
매우 매우 풀기 싫었던 문제입니다...ㅎ
좌표가 너무 이상했어요... 제가 좌표를 다루는 방식과는 너무 달라서 좌표 고정시키는 데 고생을 좀 했습니다.
근데 좌표를 고정시키니깐 거짓말처럼 호로록 풀리더라구요
좌표 다른 것 만 빼면 그렇게 어렵지는 않은 문제입니다.
근데 좌표 바꾸는게 제일 어려운;;;;

