문제
어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 곱을 구하려 한다. 만약에 1, 2, 3, 4, 5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 곱을 구하라고 한다면 240을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 곱을 구하라고 한다면 48이 될 것이다.
입력 조건
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1 번째 줄까지 세 개의 정수 a,b,c가 주어지는데, a가 1인 경우 b번째 수를 c로 바꾸고 a가 2인 경우에는 b부터 c까지의 곱을 구하여 출력하면 된다.
입력으로 주어지는 모든 수는 0보다 크거나 같고, 1,000,000보다 작거나 같은 정수이다.
출력 조건
첫째 줄부터 K줄에 걸쳐 구한 구간의 곱을 1,000,000,007로 나눈 나머지를 출력한다.
정답
Python
import sys
div_num = 1000000007
n, m, k = map(int, sys.stdin.readline().rstrip().split())
tree = [0 for _ in range((n + 1) * 4)]
g = [int(sys.stdin.readline().rstrip()) for _ in range(n)]
def init_tree(start: int, end: int, node: int):
if start == end:
tree[node] = g[start]
else:
mid = (start + end) // 2
tree[node] = (init_tree(start, mid, node * 2) * init_tree(mid + 1, end, node * 2 + 1)) % div_num
return tree[node]
def prefix_mul(start: int, end: int, node: int, left: int, right: int):
if left > end or right < start:
return 1
if left <= start and end <= right:
return tree[node]
mid = (start + end) // 2
return (prefix_mul(start, mid, node * 2, left, right) * prefix_mul(mid + 1, end, node * 2 + 1, left, right)) % div_num
def update_tree(start: int, end: int, node: int, index: int, diff: int):
if index > end or index < start:
return
if start == end:
tree[node] = g[start]
return
mid = (start + end) // 2
update_tree(start, mid, node * 2, index, diff)
update_tree(mid + 1, end, node * 2 + 1, index, diff)
tree[node] = tree[node * 2] * tree[node * 2 + 1] % div_num
init_tree(0, n - 1, 1)
for i in range(m + k):
a, b, c = map(int, sys.stdin.readline().rstrip().split())
if a == 2:
print(prefix_mul(0, n - 1, 1, b - 1, c - 1))
else:
if g[b - 1]:
diff = c / g[b - 1]
g[b - 1] = c
else:
diff = c
g[b - 1] = c
update_tree(0, n - 1, 1, b - 1, diff)
설명
기존에 구간합을 구하던 세그먼트 트리의 응용형입니다!!
하지만 구간합을 구하는 것 보다 신경써야하는 부분이 존재하죠...
1. N개의 수 중 하나가 0에서 다른 수로 변경될 때
원래 구간합을 구할 때, 수의 변경이 일어날 경우 두 수의 차를 세그먼트 트리에 더해주면서 갱신시켰습니다.
이 문제는 구간곱이니 두 수의 차가 아닌 두 수의 비율을 곱해주면 되겠죠
하지만 여기서 문제가 생깁니다.
g = [1, 0, 3, 4, 5] 라는 리스트를 세그먼트 트리로 만들어 보겠습니다!
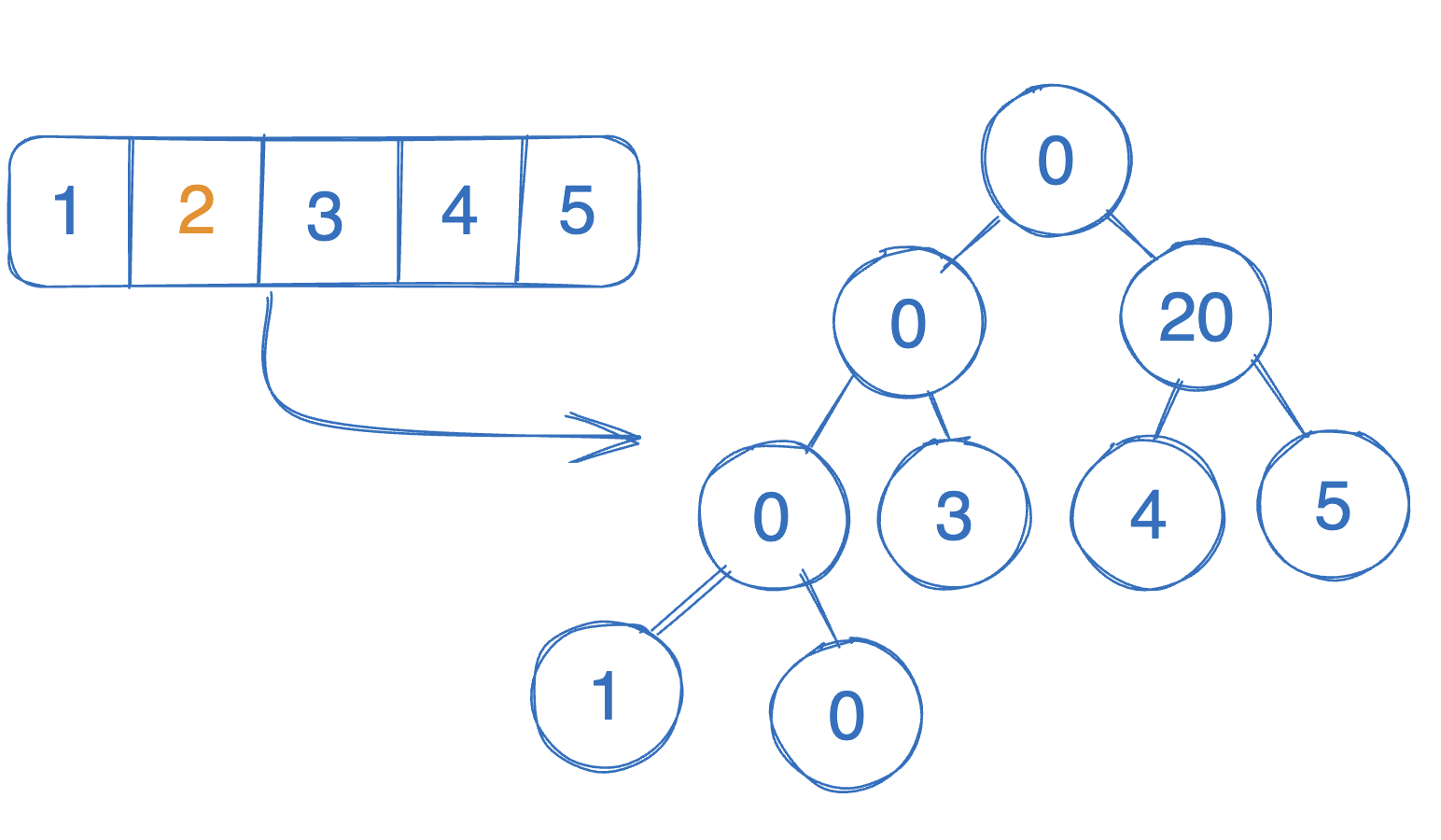
여기서 두 번째 인덱스를 0 -> 2로 바꿀 경우
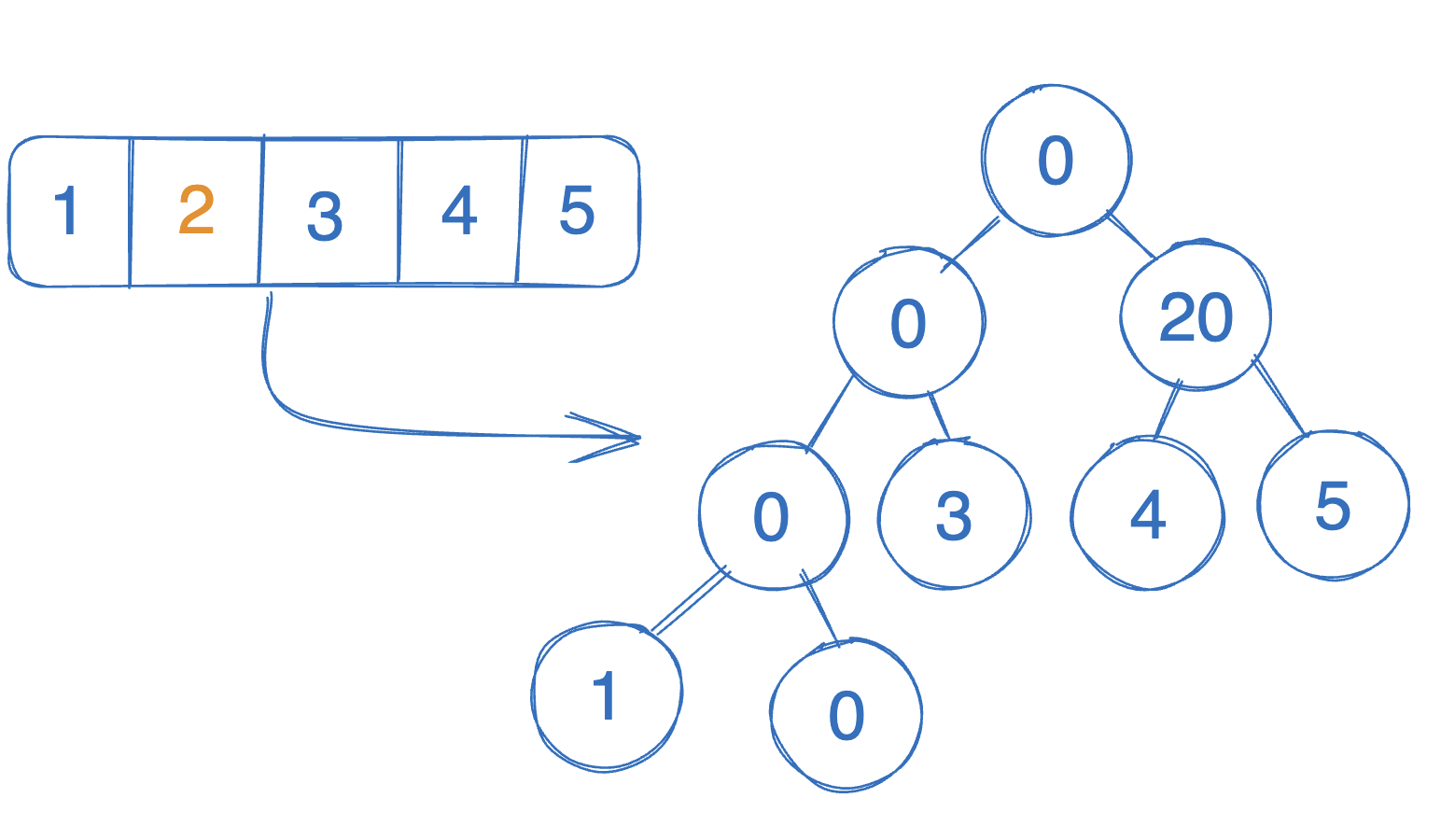
위와 같이 바뀌기를 원하겠죠!!
하지만 기존의 구간합 코드를 그대로 바꾸면 원래 배열만 변하고 트리에는 변화가 있지 않습니다
tree[node] *= diff # 기존에는 += 
배열을 바꿔도 트리는 그대로다
그 이유는 원래 로직은 트리에 변화를 주면서 내려가는 것인데 0에다가는 뭐를 곱해도 0이 나오기 때문이죠!!
하지만 내려가면서 할 수 있는 일은 없습니다.
값을 어디다가 저장해 놓은 것도 아니고 현재 값은 0이라 뭐를 곱해도 다시 0이 나올 것이기 때문이죠
그러면 언제 어떻게 트리의 노드를 바꿔야 할까요??
일단 내려갈 때가 아니라 다시 올라올 때 값을 변경시켜야 합니다.
그리고 해당 노드는 말단 노드인지 아닌지에 따라서 행동이 달라지죠
- 말단 노드일 경우 (
start == end) : 현재 노드는 말단 노드이므로 리스트에서 값을 가져와야합니다. 그냥 곱해주면 0 일 경우에는 아무런 효과가 없기 때문이죠
if start == end:
tree[node] = g[start]
return- 말단 노드가 아닐 경우 : 자식 노드의 값을 이용해서 본인의 값을 초기화해줍니다. 자식 노드의 값은 무조건 초기화가 되어 있으므로 유의미한 변화가 가능한 것이죠
tree[node] = tree[node * 2] * tree[node * 2 + 1] % div_num또, diff를 처리할 때도 현재 리스트 안의 값을 생각해줘야 합니다.
diff = 변경될 값 / 현재 값 으로 계산되는데, 현재 리스트에 저장된 값이 0이면 divide by 0 문제가 생기겠죠..!!!
그래서 diff 도 예외 처리를 해줘야 합니다.
if g[b - 1]:
diff = c / g[b - 1]
g[b - 1] = c
else:
diff = c
g[b - 1] = c2. prefix_mul 에서 index가 범위를 벗어날 때 0을 리턴할 경우
if left > end or right < start:
return 0부분합에서는 범위를 벗어나면 0을 리턴해줍니다. 이러면 리턴된 값을 더해줘도 아무런 일이 일어나지 않죠
하지만 곱할 경우에는 얘기가 역시 달라집니다.
합의 항등원은 0이지만, 곱의 항등원은 1이기 때문이죠
따라서 위 코드는 이제 1을 리턴해 줘야 합니다
if left > end or right < start:
return 1느낀 점
처음에는 그냥 구간합문제 코드를 그대로 옮기면 되는 줄 알고 바로 복붙했다가, 이런 저런 예외 때문에 생각보다 시간을 쏟은 문제입니다.
역시 저의 알량한 생각을 고쳐주더라고요
다만 역시 세그먼트 트리의 개념을 잘 이해하면 막 그다지 어렵지는 않은 문제 같았습니다(워냑 기본 문제라 그런지...)

