[알고리즘 / 백준] 트리의 지름 알아보기 (BOJ 1967/ BOJ 1167)

"트리에 존재하는 모든 경로 중 가장 긴 것의 거리" 를 구하는 문제를 마주쳤을 때, 어떤 방식으로 이를 해결해야 할까?

브루트포스적인 접근 방식으로 bfs(넓이 우선 탐색)을 통해 모든 정점에서의 최대 거리를 구해야 할까?

고민을 하던 중 주변의 도움을 받아 알게 된 해결 방법을 공부해보고자 한다.

프로그래밍을 공부하는 학생이 지식 정리 및 공유를 위해 작성한 글으로, 정확하지 않은 내용이 있을 수 있습니다. 지적과 지식 공유는 환영합니다!

트리란 ?

트리 는 그래프에 포함되어 있는 개념이다.
그래프 중 사이클을 이루지 않고 모든 노드가 연결되어 있는 그래프를 트리라고 한다.

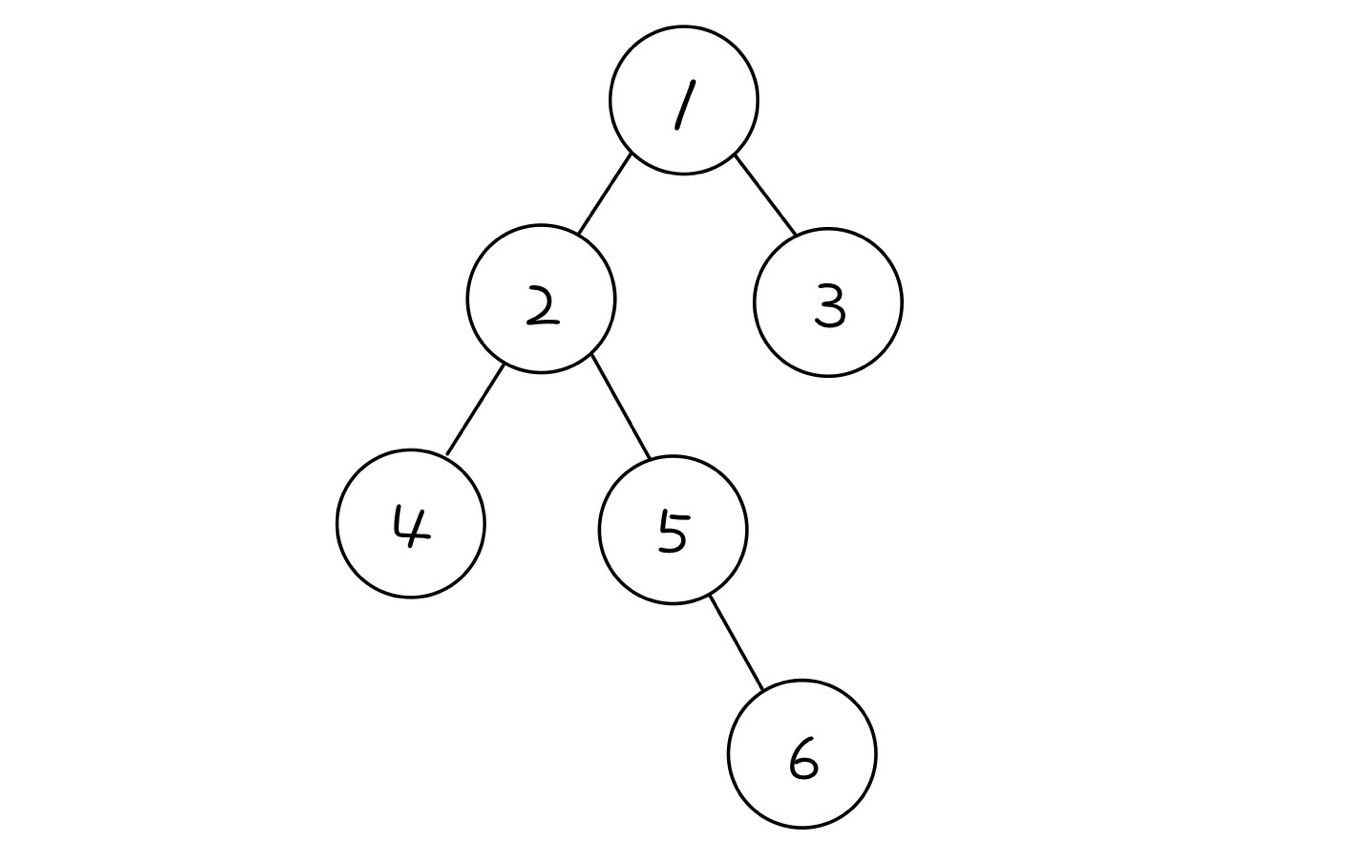
위와 같은 꼴이 트리의 대표적 예시이다.

트리의 지름

위의 모양새를 가진 트리의 지름은 무엇이라고 할 수 있을까?

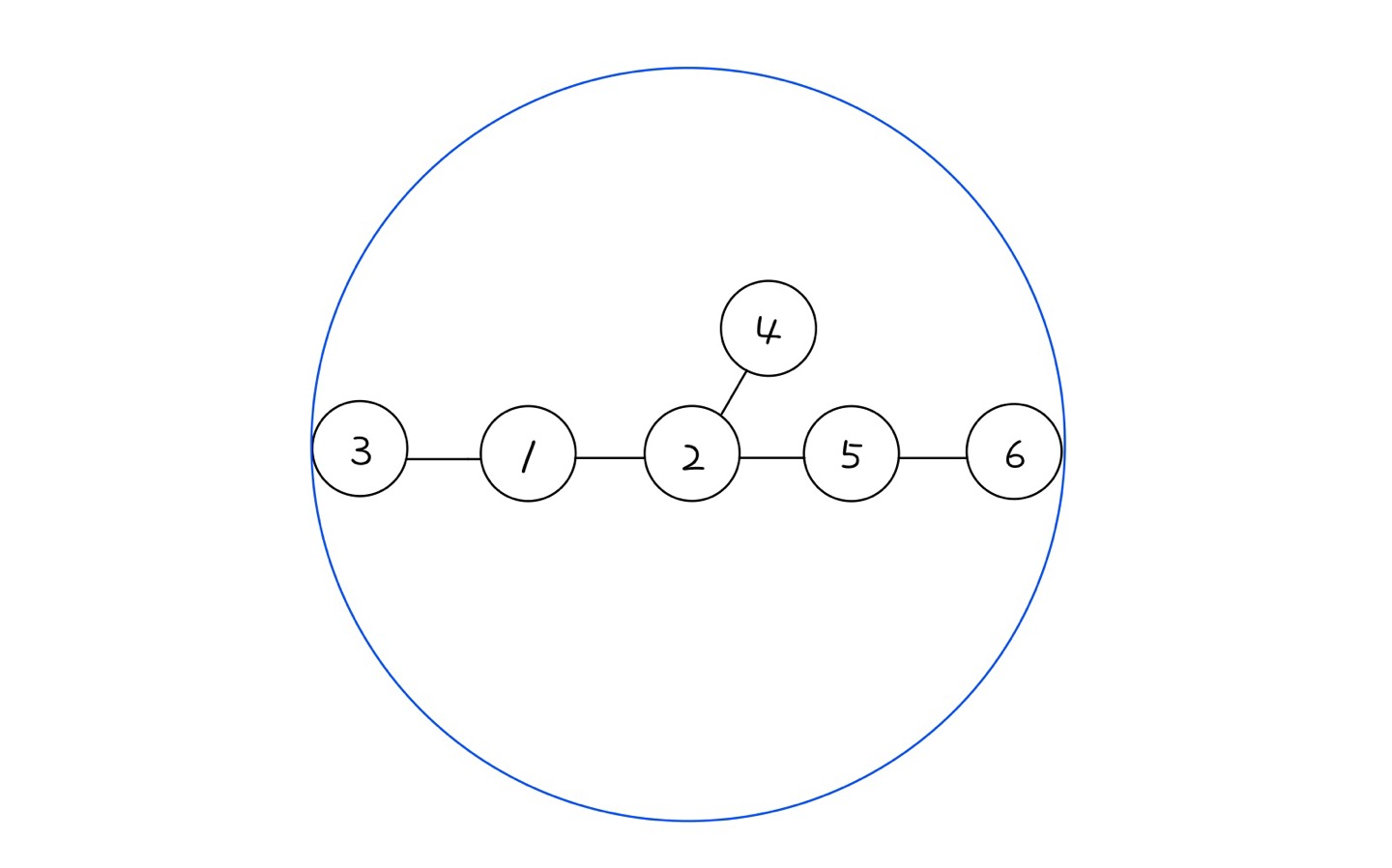
노드 3과 노드 6을 연결하는, 가장 긴 경로가 바로 이 트리의 지름이 된다고 할 수 있겠다.
위 경로는 이 트리에서 가장 긴 거리이기 때문에, 다른 모든 노드들은 위 두 노드를 지름으로 갖는 원 안에 존재한다.

트리의 지름 구하는 법

트리의 지름을 구하는 방법은 다음과 같다.

1. 임의 노드 $n$ 에서 가장 먼 노드 $u$ 를 구한다.
2. 노드 $u$ 에서 가장 먼 노드 $v$ 를 구한다.
3. 노드 $u$ 와 $v$ 사이의 거리가 트리의 지름이다.

이때, 가중치를 가지는 트리인 경우, 가중치가 가장 큰 경로가 거리가 먼 것이라고 생각하면 된다.

트리의 지름 증명

해결 방법은 꽤 단순하다고 할 수 있으나, 어떻게 그것이 최장거리이자 트리의 지름인지는 단번에 이해하기 힘들다.
나의 경우도 이해하는 데 꽤 시간이 걸렸는데, 그 과정에서 가장 도움이 많이 되었던 포스트를 소개하고자 한다.

https://blog.myungwoo.kr/112
감사합니다 :-)

위 포스트를 기반으로, 내가 이해한 바를 정리해보면 다음과 같다.

위의 방법으로 구한, 트리의 지름으로 가정하는 노드 $a$ 와 노드 $b$ 가 있다. 그리고 실제 트리의 지름인 노드 $u$ 와 노드 $v$ 가 있다.

이 네가지 노드는 다음과 같은 관계일 수 있다.

1. 노드 $a$ 가 노드 $u$ 혹은 노드 $v$ 중 하나와 일치한다
   즉, 노드 $a$ 는 트리의 지름의 양 끝 노드 중 하나이다.

2. 노드 $b$ 가 노드 $u$ 혹은 노드 $v$ 중 하나와 일치한다
   즉, 노드 $b$ 는 트리의 지름의 양 끝 노드 중 하나이다.

3. 노드 $a$ 와 노드 $b$ 둘 다 트리의 지름의 양 끝 노드가 아니다.
   
   

1번과 2번, 노드 $a$ 또는 노드 $b$가 트리의 지름을 이루는 양 끝 노드라고 하면, 각 노드로부터 가장 먼 노드인 $b$ 또는 $a$ 또한 트리의 지름의 양 끝 노드이기 때문에 이 방법은 옳은 방식일 것이다.

따라서, 3번의 경우가 존재하지 않음을 증명해낸다면, 해당 방법은 옳다고 할 수 있다.
3번일 때, 두 가지 경우를 생각할 수 있다.

1. 실제 트리의 지름과, 우리가 구한 트리의 지름의 경로가 일부 겹칠 때
   
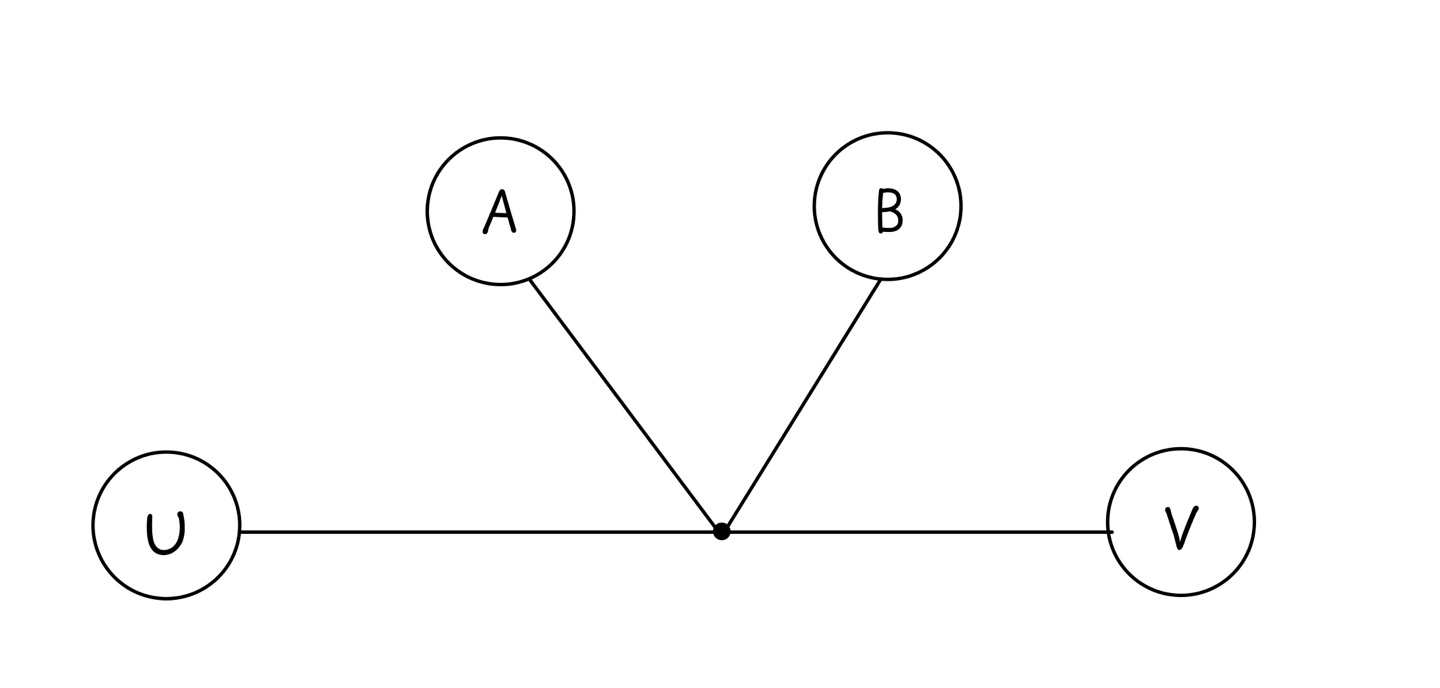
   겹치는 노드를 $n$ 이라고 하자.
   위 방식으로 구했을 때, 임의의 노드 $a$가 있고, $a$와 $b$의 거리는 최대가 되기 때문에 노드 $b$가 구해졌다.
   그렇다는 것은 노드 $n$과 노드 $b$ 사이의 거리는 노드 $n$과 $u$ 사이의 거리, 노드 $n$과 $v$ 사이의 거리의 최댓값과 같거나 크다는 뜻이다.
   $\overline{nb} \geq max(\overline{nu}, \overline{nv})$

• 같은 경우
  $\overline{nb} = \overline{nu}$ 가 된다면, $b$는 트리의 지름을 이루는 양 끝 노드 중 하나가 될 것이다. 이로부터 가장 먼 노드는 자연스레 $v$가 될 것이고, 따라서 $a$ 와 $b$ 는 트리의 지름을 이루게 된다.
• 큰 경우
  $\overline{nu} + \overline{nv}$ 은, 자명한 트리에서 가장 긴 경로이다. 이보다 큰 $\overline{nb}$ 는 존재할 수 없다.
  만약 $\overline{nb}$ 가 더 크다면 트리의 지름은 $\overline{bu}$ 혹은 $\overline{bv}$ 여야 한다.
  따라서 큰 경우는 존재할 수 없다.

2. 실제 트리의 지름과, 우리가 구한 트리의 지름의 경로가 겹치지 않을 때
   
   트리는 모든 노드가 연결되어 있기 때문에 (동떨어진 그래프는 존재하지 않는다), 다음과 같은 모양을 가지고 있을 것이다.
   노드 $a$ 에서 가장 먼 노드가 $b$ 라는 것은,
   $\overline{nb} \geq \overline{nm} + max(\overline{mu}, \overline{mv})$
   를 만족한다는 뜻이 된다.
   그 말은 즉슨 $\overline{mu}, \overline{mv}$ 보다 $\overline{mb}$ 가 훨씬 길다는 뜻이고, 이는 곧 $\overline{uv}$ 가 트리의 지름이라는 가정과 모순된다.

따라서 3번은 존재하지 않으며, 위 방법은 옳다.

트리의 지름 적용

증명과 이해를 하는 과정은 힘들었지만, 이를 적용하는 것은 이해보다 쉬울 지도 모른다.
트리의 지름을 구하는 방법과 그래프의 넓이 우선 탐색(bfs)을 이용해 다음 문제를 풀어보았다.

백준 문제 링크

[BOJ 1167: 트리의 지름] https://www.acmicpc.net/problem/1167
[BOJ 1967: 트리의 지름] https://www.acmicpc.net/problem/1967

두 문제는 노드 개수의 범위가 10배 정도 차이나는 것과 입력 방식이 다르다는 점을 제외하고 거의 일치하다고 볼 수 있다. 트리의 지름을 이용하면, bfs를 두 번만 사용하면 되기 때문에, 두 문제를 무난하게 해결해낼 수 있다.

접근 방식 / 풀이

1967번 의 경우, 임의의 노드에서 시작하기 때문에, 입력을 받은 후, 양방향으로 각각의 간선을 저장해줘야 한다. 1167번 은 두 방향 모두 입력으로 주어지기에 크게 신경쓰지 않아도 된다.

나의 경우, bfs (넓이 우선 탐색)를 진행할 때, pair에 노드 번호, 경로의 가중치를 저장한 queue를 사용했다. queue에서 노드를 pop할 때 해당 노드의 가중치의 값이 최대인 경우 미리 저장해둔 뒤, bfs가 끝나면 가중치가 최대인 노드의 정보를 리턴값으로 주었다.

따라서, 처음은 임의의 노드로 bfs를 진행하고, 리턴값으로 받은 가중치가 최대인 노드에서부터 bfs를 다시 진행하여 해당 노드로부터 가장 먼 노드까지의 가중치를 출력하여 해결했다.

답안 코드 링크 (Github)

Github Solution Link; BOJ 1167
Github Solution Link; BOJ 1967