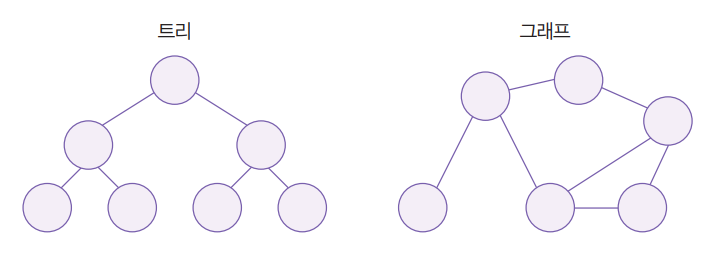
트리(Tree)
비선형 자료구조이며, 부모 노드와 자식 노드간의 연결로 이루어진 자료 구조. 계층이자 그룹이다.
용어
- 루트 노드 (root node): 부모가 없는 노드로 최상단의 노드를 의미한다.
- 단말 노드 (leaf node): 자식이 없는 노드로 터미널 (terminal) 노드라고도 불린다.
- 내부 노드 (internal node): 단말 노드가 아닌 노드를 칭한다.
- 형제 (sibling): 같은 부모를 갖는 노드들을 말한다.
- 링크 (link): 노드와 노드사이를 잇는 선이다. edge, branch라고도 불린다.
- 깊이 (depth): 루트 노드에서 한 노드에 도달하기까지의 링크 수를 의미한다.
- 레벨 (level): 같은 깊이를 가지는 노드들의 집합.
- 차수 (degree): 한 노드가 가지는 링크의 수
특징
- N개의 노드를 갖는 트리는 항상 N-1개의 링크를 가진다.
- 한 노드에서 어떠한 노드로 가는 길은 한 개의 유일한 경로를 가진다.
트리의 종류
이진 트리 (Binary Tree)
- 자식 노드를 최대 2개 까지만 가질 수 있는 트리이다.
완전 이진 트리 (Complete Binary Tree)
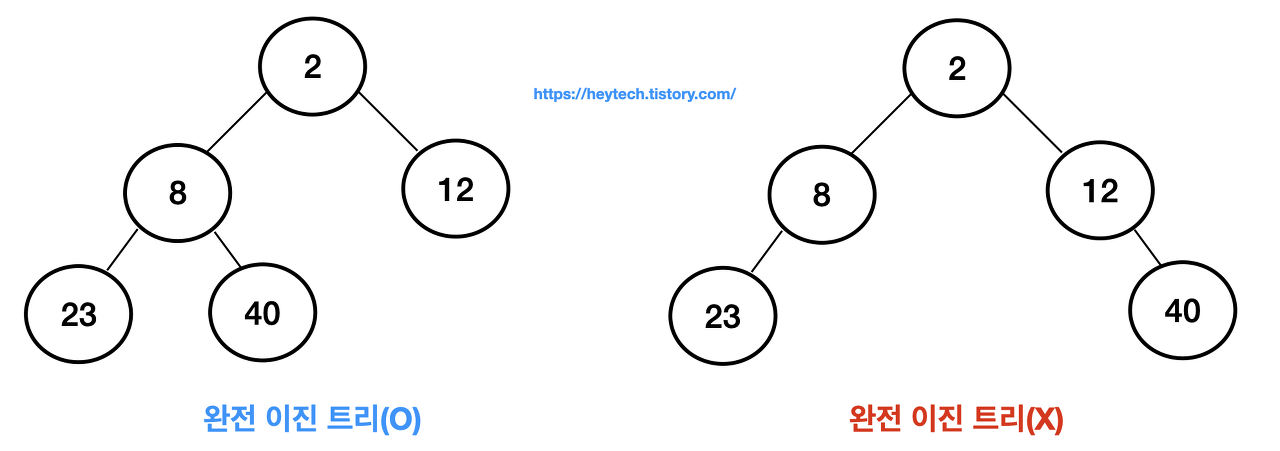
- 왼쪽 자식 노드부터 채워지며 단말 노드를 제외한 모든 자식 노드가 채워져 있다.
Full Binary Tree
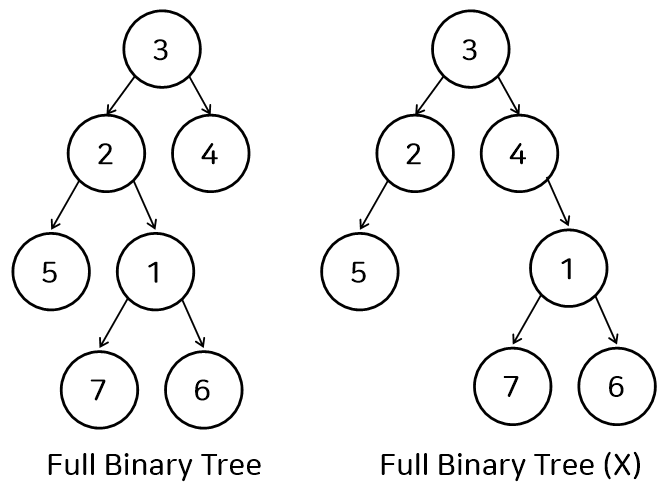
- 모든 노드가 0개 혹은 2개의 자식 노드를 가지는 트리
포화 이진 트리 (Perfect Binary Tree)
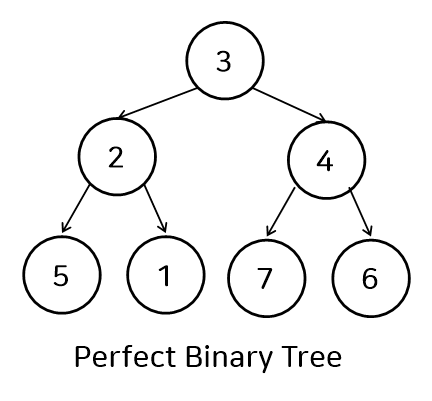
- 모든 레벨이 노드로 꽉차 있으며 Full Binary Tree의 성질을 동시에 만족하는 트리
- level의 n이라 할 때, 노드의 개수는 2^n-1 개 이다.
이진 탐색 트리 (Binary Search Tree)
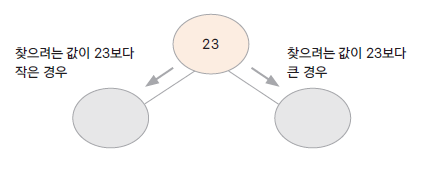
- 이진 트리의 조건을 만족하면서 아래의 정렬 조건을 만족하는 트리이다.
- 모든 노드의 값은 유일하다.
- 부모의 값이 왼쪽 자식의 노드보다 크다.
- 부모의 값이 오른쪽 자식의 노드보다 작다.
트리순회, Binary Tree Traversals
Tree의 Node들을 지정된 순서대로 “방문”하는 것
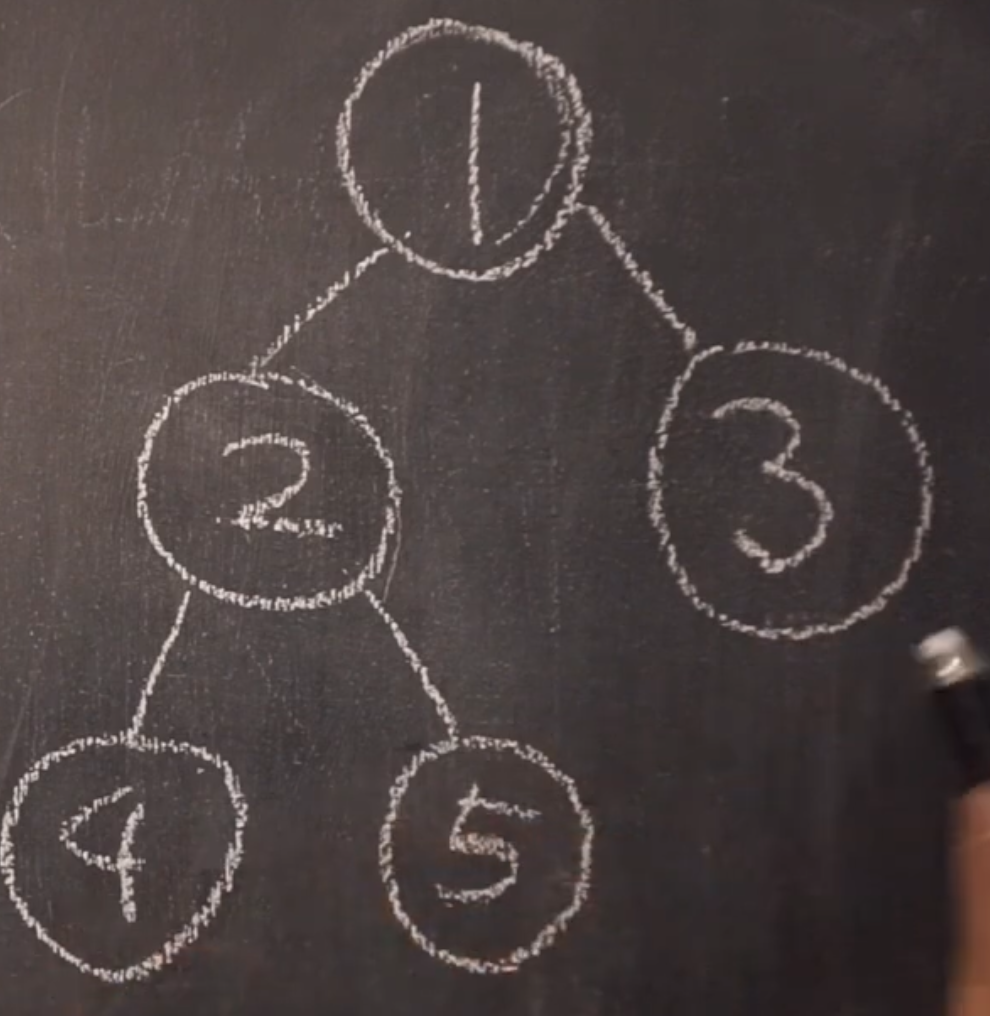
- 전위순회, preorder ( root, left, right)
- 1 -> 2 -> 4 -> 5 -> 3 - 중위순회, Inorder ( left, root, right)
- 4 -> 2 -> 5 -> 1 -> 3 - 후위순회, Postorder ( left, right, root)
- 4 -> 5 -> 2 -> 3 -> 1
구현해보기 java
package treeStudy;
class Node {
int data;
Node left;
Node right;
}
class Tree {
public Node root;
public void setRoot(Node node) {
this.root = node;
}
public Node getRoot() {
return root;
}
public Node makeNode(Node left, int data, Node right) {
Node node = new Node();
node.data = data;
node.left = left;
node.right = right;
return node;
}
public void inorder(Node node) {
if(node != null){
inorder(node.left);
System.out.println(node.data);
inorder(node.right);
}
}
public void preorder(Node node) {
if(node != null) {
System.out.println(node.data);
preorder(node.left);
preorder(node.right);
}
}
public void postorder(Node node) {
if(node != null) {
postorder(node.left);
postorder(node.right);
System.out.println(node.data);
}
}
}
public class TreeImpl {
public static void main(String[] args) {
Tree tree = new Tree();
Node n5 = tree.makeNode(null, 5, null);
Node n4 = tree.makeNode(null, 4, null);
Node n3 = tree.makeNode(null, 3, null);
Node n2 = tree.makeNode(n4, 2, n5);
Node n1 = tree.makeNode(n2, 1, n3);
tree.inorder(n1);
System.out.println("======================");
tree.preorder(n1);
System.out.println("======================");
tree.postorder(n1);
}
}binary heap
힙이란 최대값이나 최소값을 찾아내는 연산을 빠르게 하기위해 고안된 완전이진트리를 기본으로한 자료구조이다
예를 들어 다음과 같은 배열이 있다고 해보자.
let arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]이 배열에서 최댓값을 구하기 위해선 배열을 모두 돌아야 하므로 시간복잡도는 O(N)을 가지게 된다. 하지만 힙을 이용하면 이 작업을 O(log N)으로 해결할 수 있게 해준다.
최소힙
자신보다 작은 값을 항상 부모 노드에 둬서 루트 노드에는 최소값이다.
최대힙
자신 보다 큰 값는 부모 노드에 둬서 루트 노드는 최대값이다.
최소힙에 노드 삽입하기
완전트리의 맨 끝에 노드를 추가한다. Complete Binary Tree 형태를 잃지 않도록 왼쪽부터 채워나간다.
노드를 추가한 직 후 정렬되지 않은 상태에서 자신의 부모와 비교해서 자신이 작으면 자리를 바꾸는 것을 노드가 루트에 도달하거나 부모노드에서 자신보다 작은 수를 만날 때까지 계속 반복한다.
한 레벨씩 루트까지 올라간다면 한번 돌때마다 절반씩 범위가 줄어드므로 O(log N)의 시간복잡도를 가진다.
최대값의 삽입은 반대로 생각하면된다.
최소힙에서 노드 꺼내오기
최소힙은 최소값을 찾기 위한 자료구조이므로 가장 작은 값을 가져온다는 듯이다. 최소값은 루트에 있으니까 가져오는건 어렵지않지만 루트의 자리에 채워줘야한다.
Complete Binary Tree의 맨마지막 노드를 루트에 채운다. 자식의 노드와 비교해서 둘 중 작은 노드와 자리를 교환한다. 자식이 자기보다 크거나 마지막 노드에 도달했을 때 멈춘다.
Trie
문자열에서 검색을 빠르게해주는 트리구조이다. 정수형자료에서 이진트리로 검색을 하면 O(log n)의 시간이 걸린다.
문자열을 검색하는 경우에는 매번노드를 방문할때마다 비교를 해야하므로 문자열의 최대길이가 M일때 O(MlogN)의 시간이 걸린다.
이 문제를 해결하기 위해서 Trie라는 트리를 이용한다.
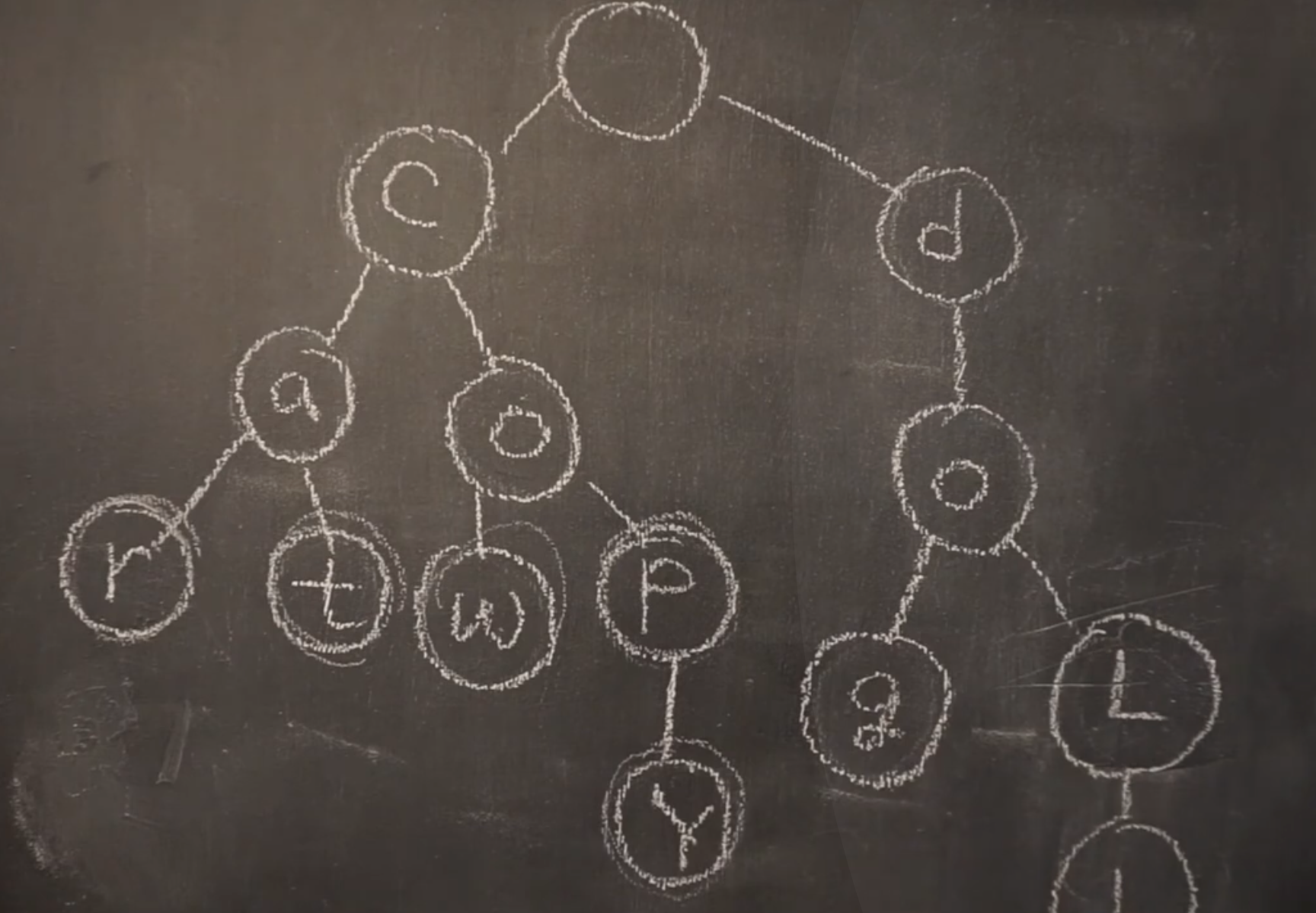
예를 들어서 사전을 만든다고 할 때, 한 글자에 level 하나씩 가도록 한다. 문자열을 한 자씩 다음 문자열은 자식노드에서 찾는 것이다. 문자열이 세로로 저장되어 있는 형태이다. car에 대한 정보를 찾고 싶을 때 c-a-r로 찾아가면 된다.
영어소문자만 허락 했을 때 모든 노드는 각 26개의 알파벳 노드를 가질 수있고 M이 문자열의 최대 길이라 할때 O(M)의 시간이 걸리는 알고리즘이다.
사용사례
- 문자열 검색 애플리케이션: 검색 엔진, 철자 검사기, 자동 완성 기능 등과 같은 문자열 검색 기능을 구현할 때 트라이를 사용할 수 있다.
- 사전 구현: 사전 데이터를 저장하고 검색하는 데에도 트라이가 사용될 수 있다. 이를 통해 사전의 단어를 빠르게 검색할 수 있다.
- IP 라우팅: IP 주소를 검색하여 라우터가 데이터를 전달하는 데 사용될 수 있다.
참고
https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
https://gnujoow.github.io/ds/2016/09/01/DS4-TreeTraversal/