- 관계 데이터 연산의 개념과 종류를 알아본다
- 일반 집합 연산자와 순수관계 연산자의 차이를 이해한다
- 일반 집합 연산자와 순수관계 연산자를 이용해 질의를 표현하는 방법을 익힌다.
관계 데이터 연산
원하는 데이터를 얻기위해서 릴레이션의 필요한 처리요구를 수행하도록 하는것이다.
연산의 사전적인 뜻은 식이 나타낸 일정한 규칙에 따라 계산하는것
관계 데이터 연산의 개념
데이터 모델 - 데이터 구조 + 연산 + 제약조건
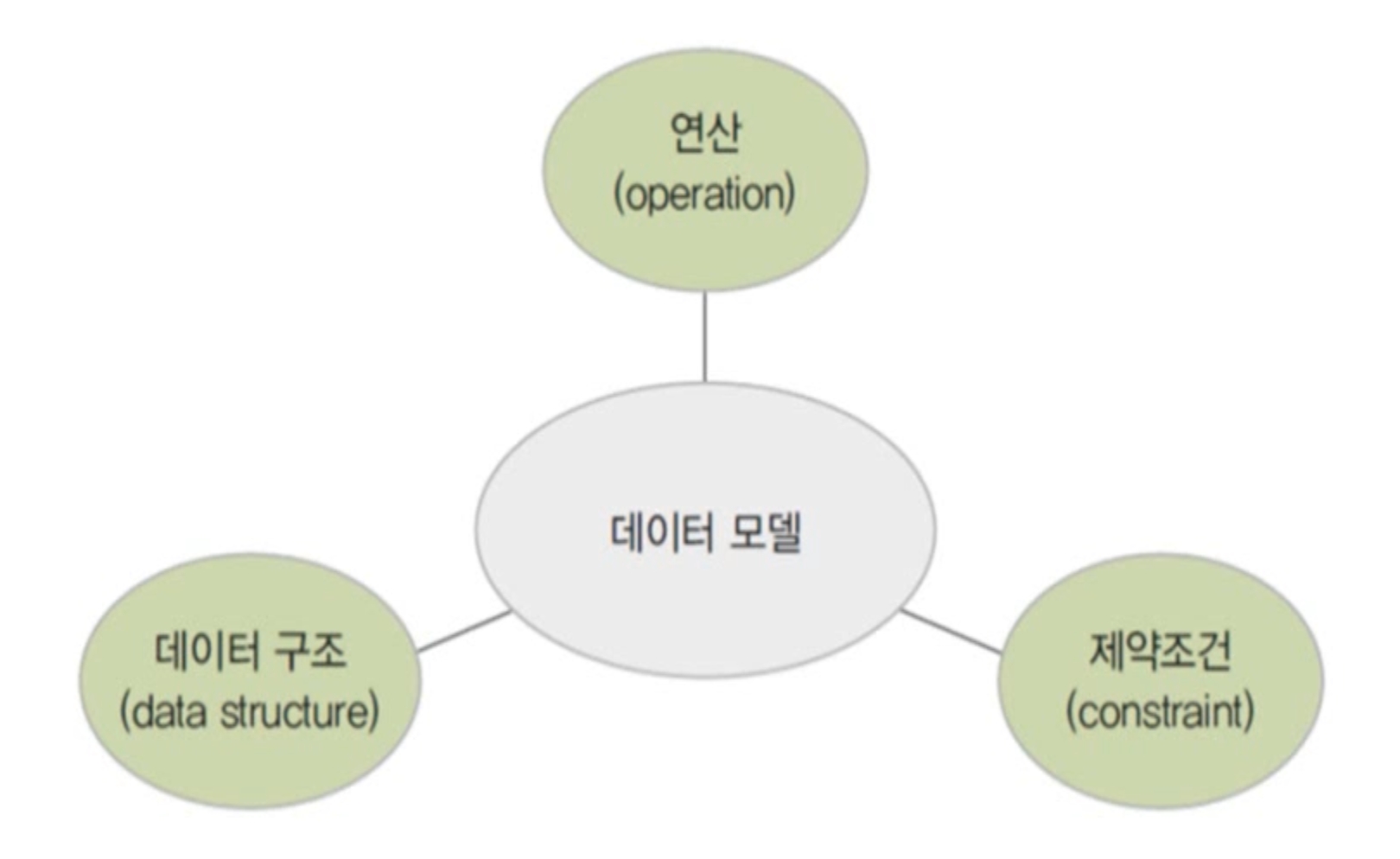
관계 데이터 연산(relational data operation)
- 관계 데이터 모델의 연산
- 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것
- 관계 대수와 관계 해석이 있음
- 기능과 표현력 측면에서 능력이 동등함
- 처리 절차를 얼마나 자세히 기술하느냐에 따라 차이를 보임

관계 대수
관계 대수(relational algebra)의 개념
- 원하는 결과를 얻기 위해 릴레이션의 처리과정을 순서대로 기술하는 언어
- 절차언어 - 릴레이션을 처리하는 연산자들의 모임
- 대표연산자 8개
- 일반 집합 연산자와 순수 관계 연산자로 분류됨 - 폐쇄 특성이 존재함
- 피연산자도 릴레이션이고 연산의 결과도 릴레이션임
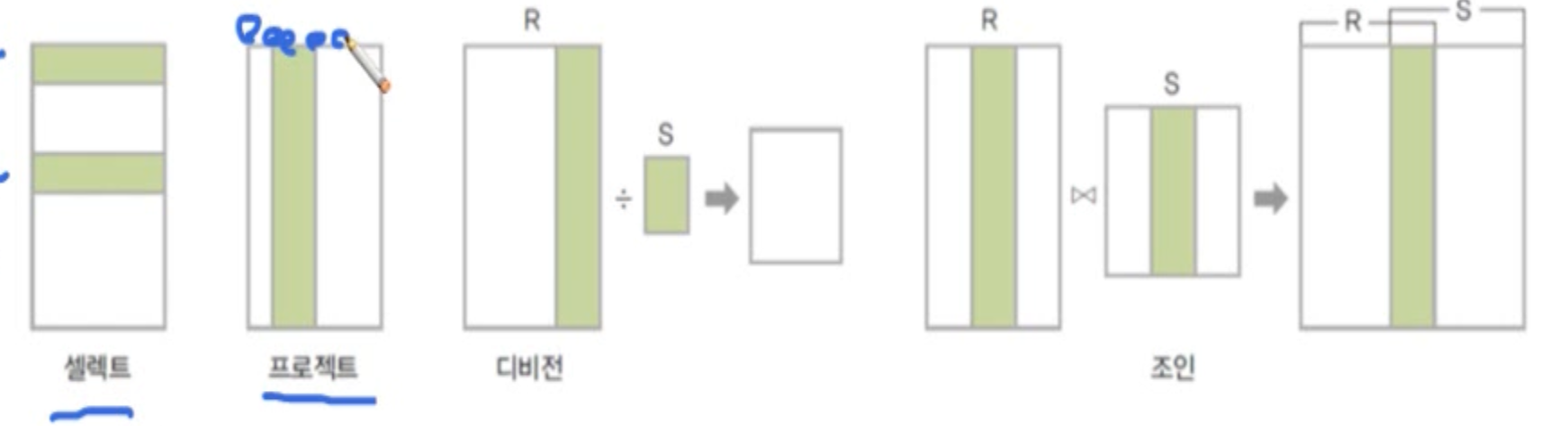
일반 집합 연산자(set operation)
- 릴레이션이 튜플의 집합이라는 개념을 이용하는 연산자
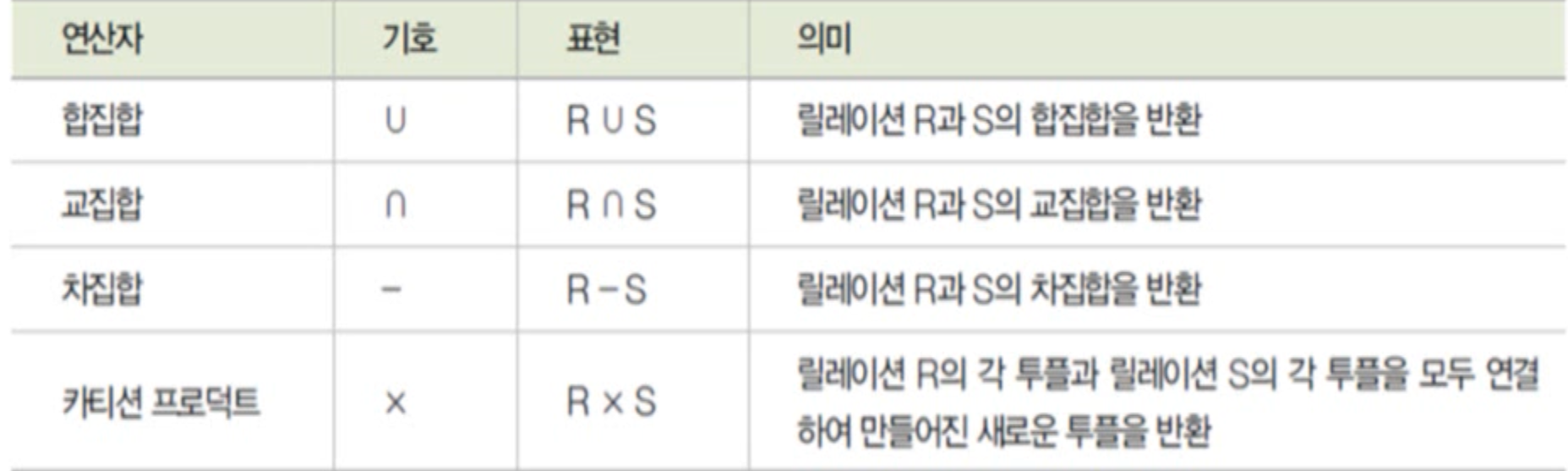
일반 집합 연산자의 기능
예)
인터파크와 G마켓의 모든 고객
인터파크와 G마켓의 공통 고객
인터파크나 G마켓만의 고객
R이 고객, S상품이면 모든 경우의수를 구하는경우 카티션 프로덕트를 사용하게된다.순수관계 연산자(relational operation)
-
릴레이션의 구조와 특성을 이용하는 연산자
예) 인터파크에서 나이가 30세 이상인 고객들을 찾고싶다 인터파크의 릴레이션의 속성이 id,전화번호로만 뽑아내고 싶은 경우
순수 관계 연산자의 기능
일반 집합 연산자의 특성
- 피연산자가 두 개필요함
- 두개의 릴레이션을 대상으로 연산을 수행 - 합집합, 교집합, 차집합은 피연산자인 두 릴레이션이 합병이 가능해야함
- 합병가능(union-compatible) 조건- 두 릴레이션의 차수가 같아야함
- 두 릴레이션에서 서로 대응되는 속성의 도메인이 같아야함
합병이 불가능한 예
합병이 가능한 예
일반집합 연산자
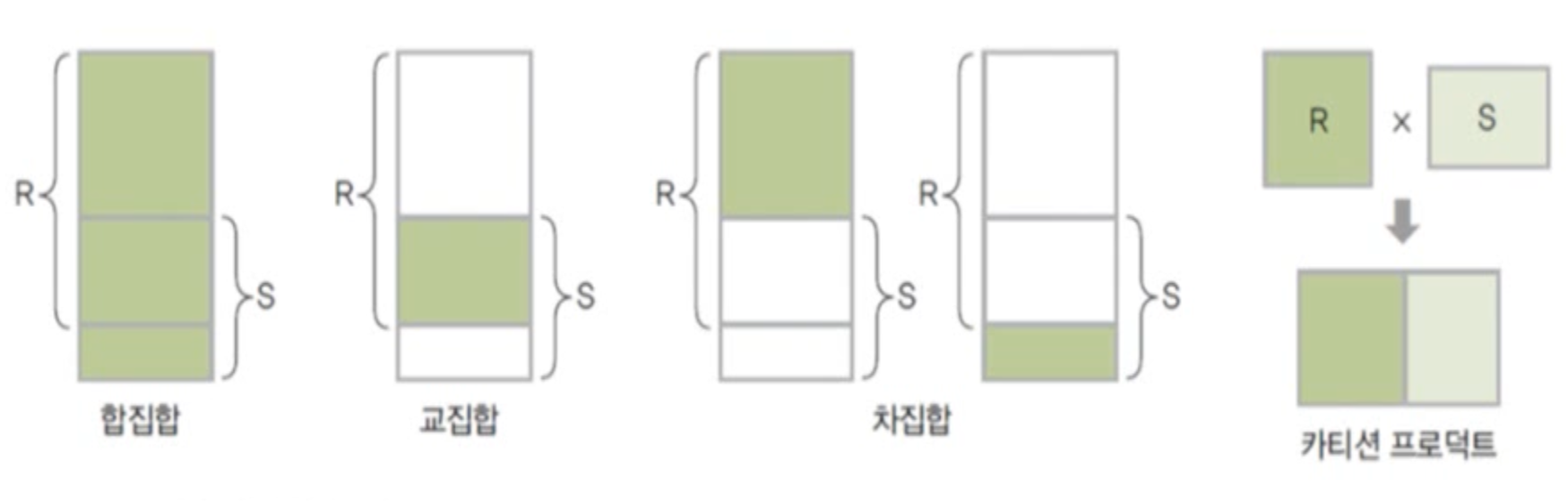
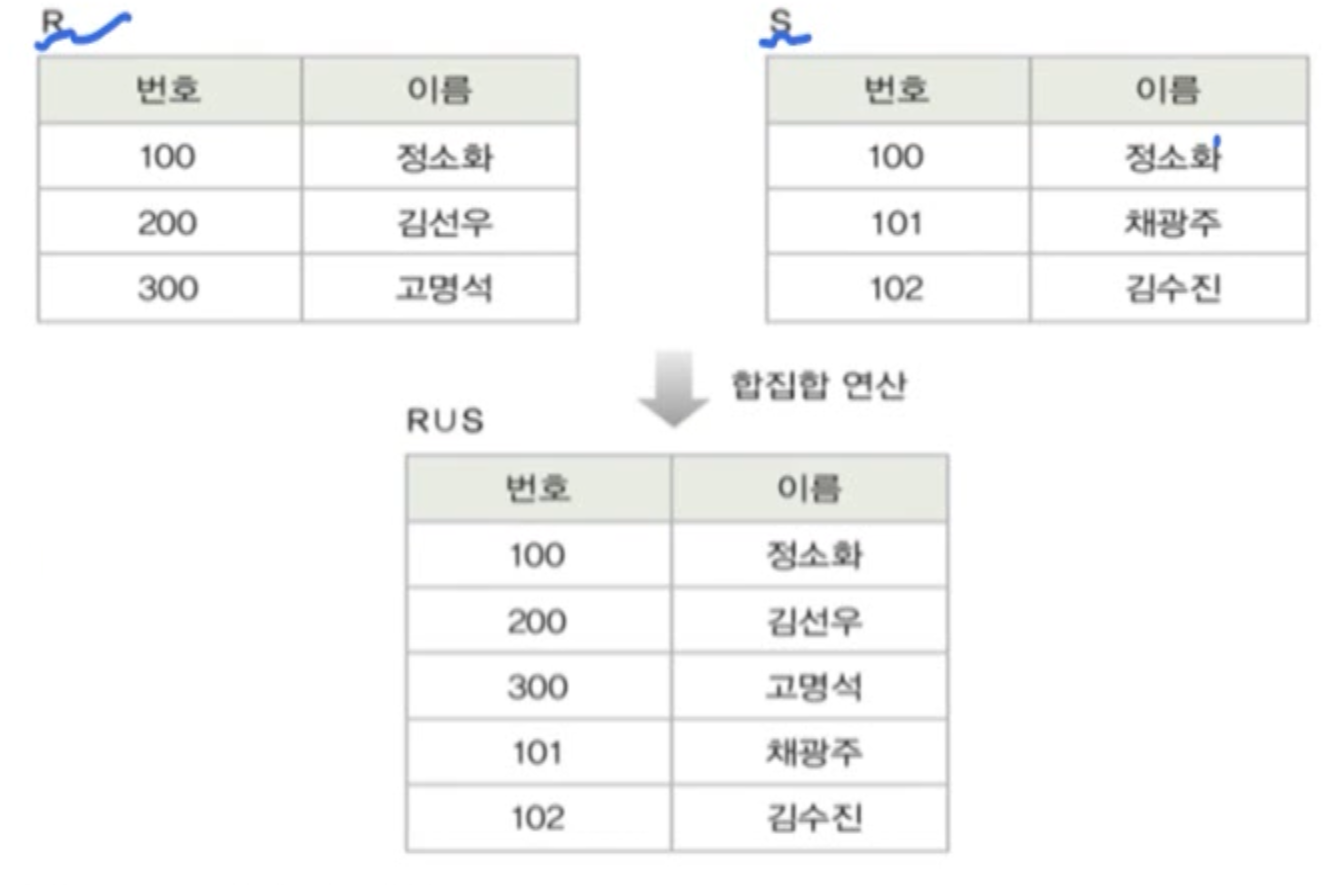
합집합(union)
-
합병 가능한 두 릴레이션 R과 S의 합집합 :
- 릴레이션 R에 속하거나 릴레이션 S에 속하는 모든 튜플로 결과 릴레이션 구성합집합 연산의 예
-
결과 릴레이션의 특성
- 차수는 릴레이션 R과 S의 차수는 같음- 카디널리티는 릴레이션 R과 S의 카디널리티를 더한 것과 같거나 적어짐
-
교환적 특징이 있음
- R∪S = S∪R -
결합적 특징이 있음
- (R∪T)∪S = (S∪T)∪R
교집합(intersection)
-
합병 가능한 두 릴레이션 R과 S의 교집합 :
- 릴레이션 R과 릴레이션 S에 속하는 모든 튜플로 결과 릴레이션 구성
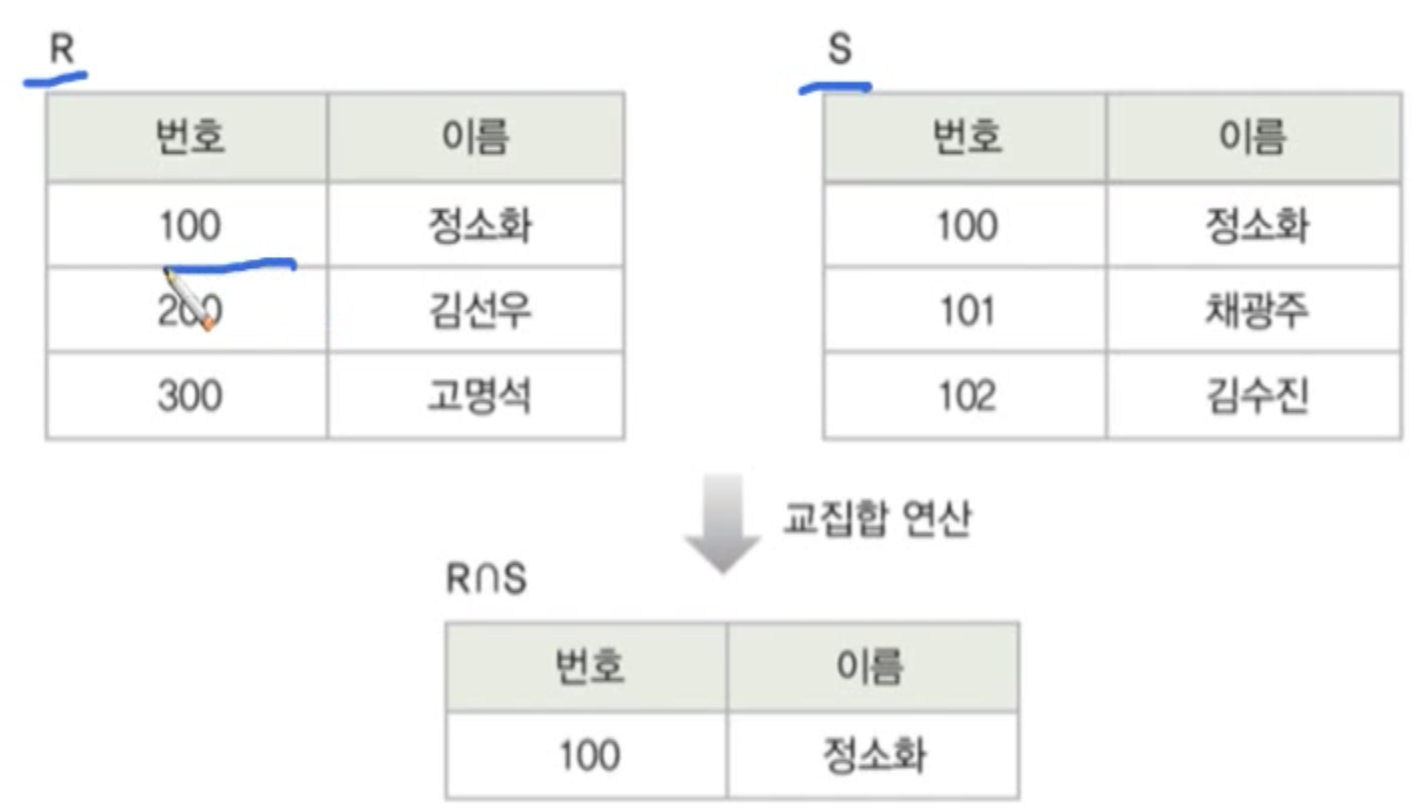
-
결과 릴레이션의 특성
- 차수는 릴레이션 R과 S의 차수과 같음
- 카디널리티는 릴레이션R과 S의 어떤 카디널리티보다 크지않음 -
교환적 특징이 있음
- R∩S =S∩R -
결합적 특징이 있음
- (R∩T)∩S = (S∩T)∩R
차집합(difference)
-
합병가능한 두 릴레이션 R과 S의 차집합 : R - S
- 릴레이션 R에는 존재하고 S에는 존재하지 않는 튜플로 결과 릴레이션 구성
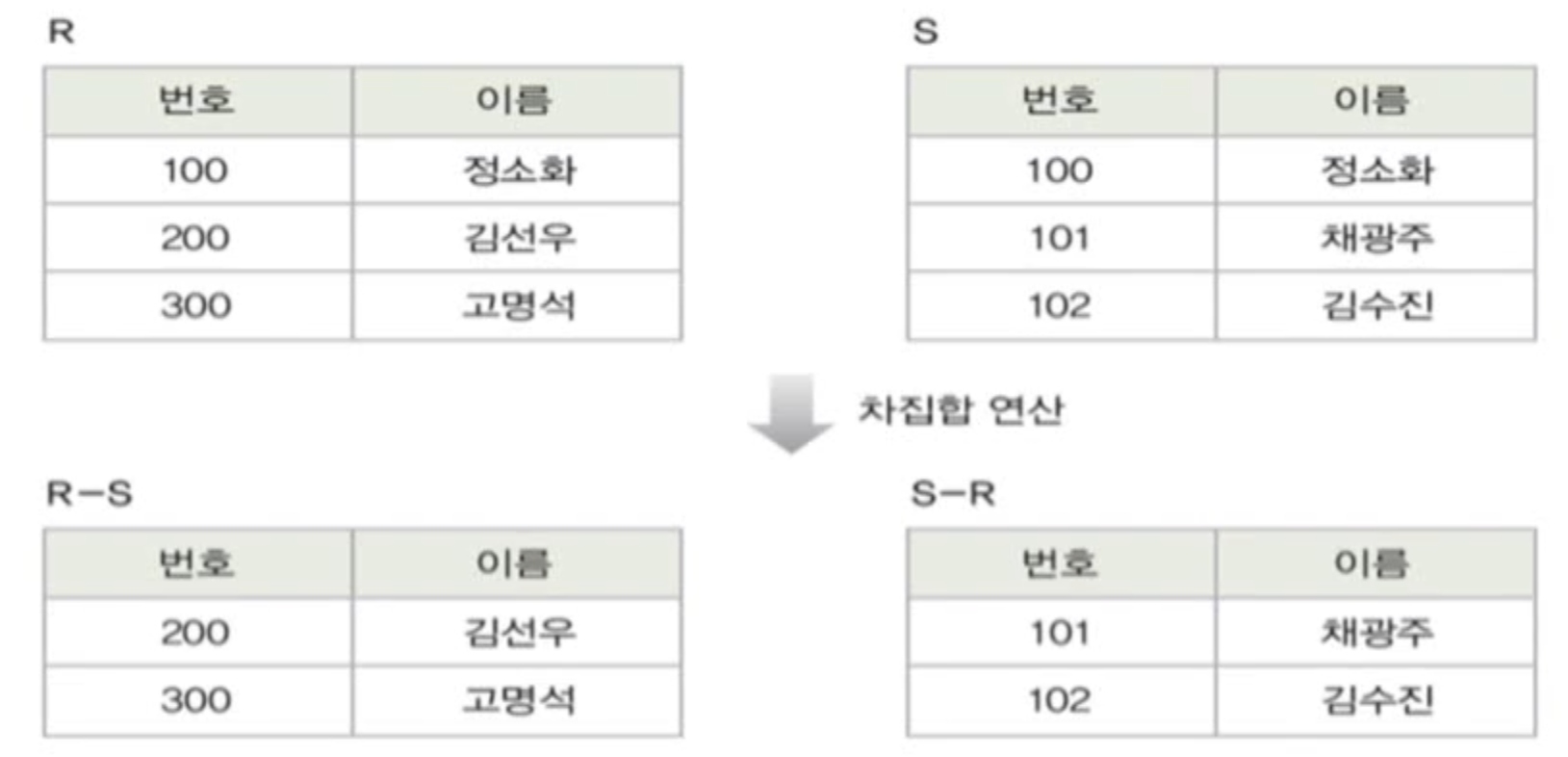
-
결과 릴레이션의 특성
- 차수는 릴레이션 R과 S의 차수와 같음
- R-S의 카디널리티는 릴레이션의 R의 카디널리티와 같거나 적음- S-R의 카디널리티는 릴레이션의 S의 카디널리티와 같거나 적음
-
교환적, 결합적 특성이 없음
카티션 프로덕트(cartesian product)
-
두 릴레이션 R과 S의 카티션 프로덕트 : RxS
- 릴레이션R에 속한 각 튜플과 릴레이션S에 속한 각 튜플을 모두 연결하여 만들어진 새로운 튜플로 결과 릴레이션을 구성
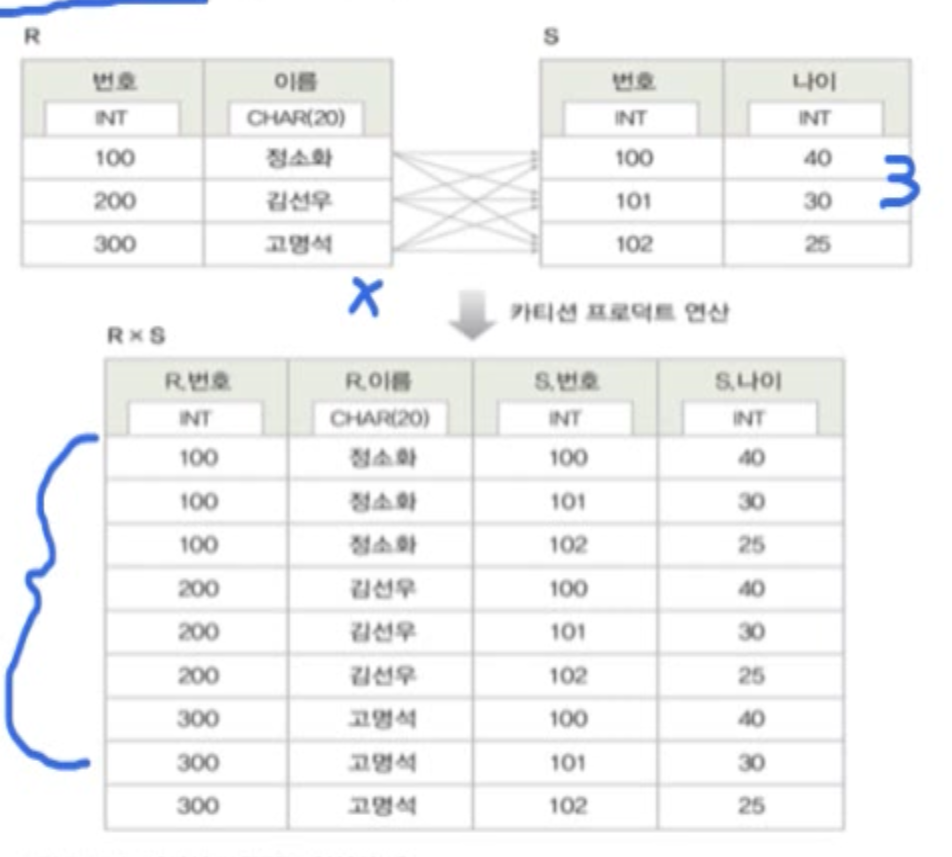
-
결과 릴레이션의 특성
- 차수는 릴레이션R과 S의 차수를 더한것과 같음
- 카디널리티는 릴레이션 R과 S의 카디널리티를 곱한것과 같음 -
교환적 특징이 있음
-
결합적 특징이 있음
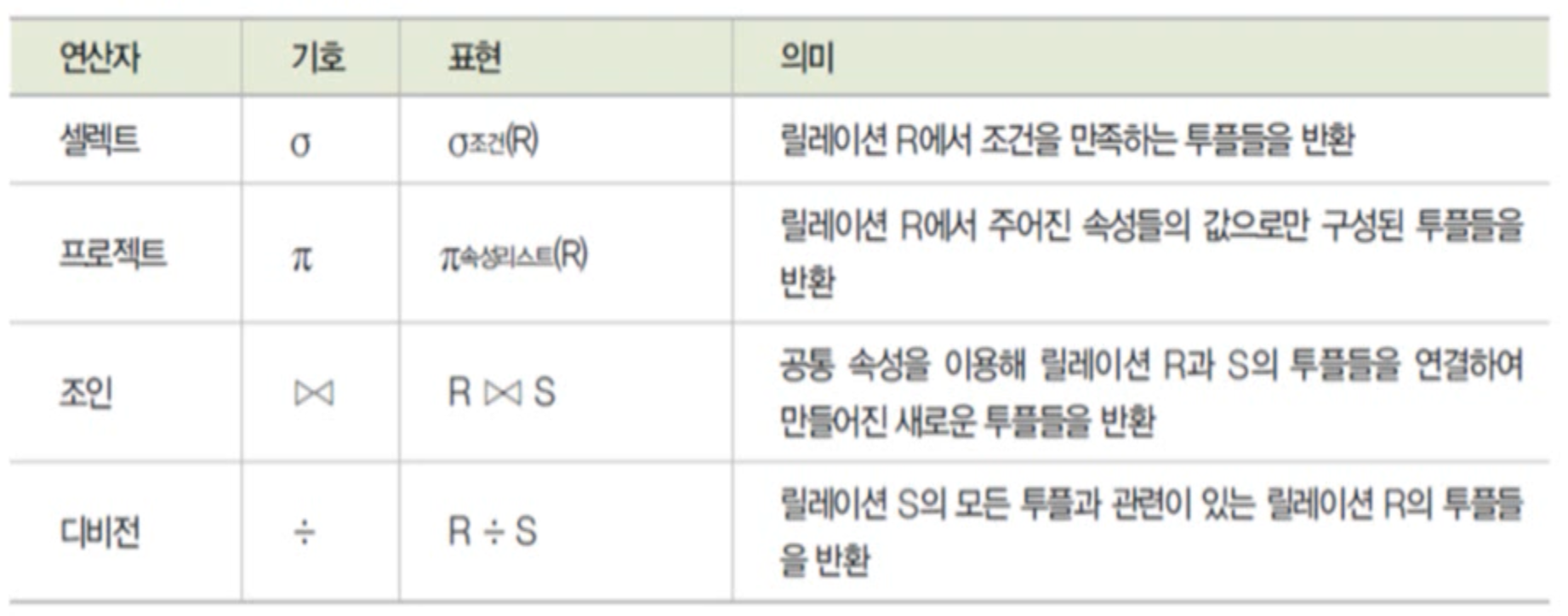
순수관계 연산자
고객 릴레이션
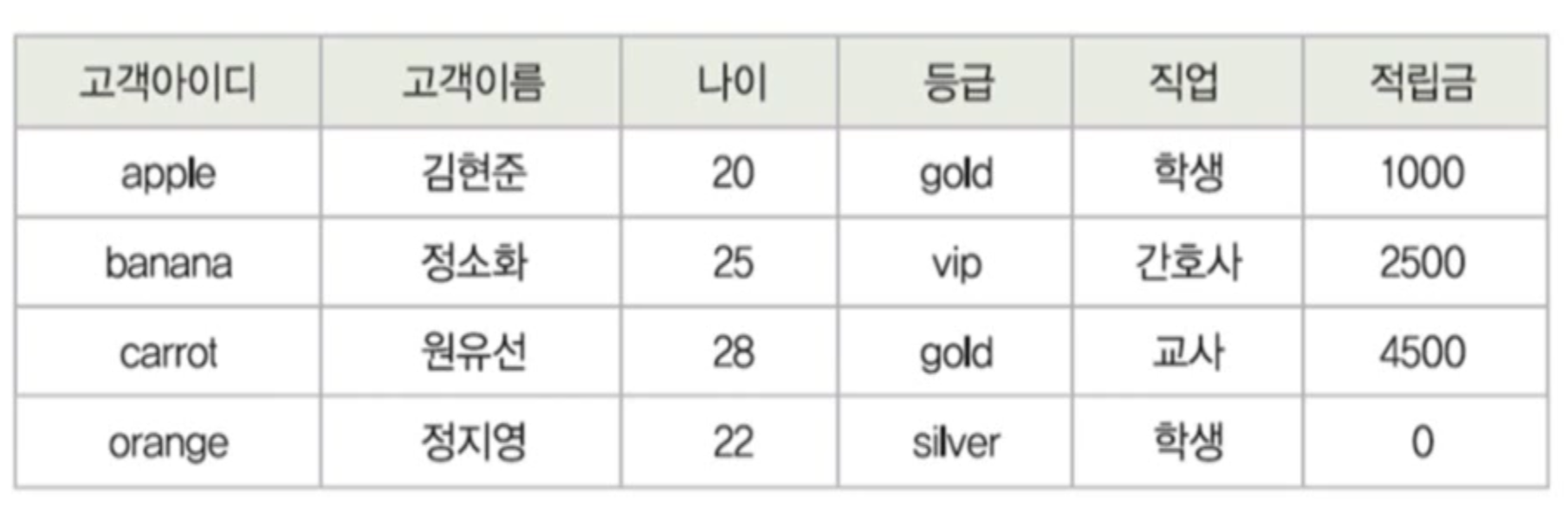
셀렉트(select)
- 릴레이션에 조건을 만족하는 튜플만 선택하여 결과 릴레이션을 구성
- 하나의 릴레이션을 대상으로 연산을 수행
- 수학적 표현법 : σ조건
- 데이터 언어적 표현법 : 릴레이션 where 조건식
- 조건식
- 비교식, 프레디킷(predicate)이라고도 함
- 속성과 상수의 비교나 속성들 간의 비교로 표현
- 비교연산자(>, <, <=, >=, =, !=)와 논리연산자(논리합=∨, 논리곱=∧, 부정=¬)를 이용해 작성
그림
-
고객 릴레이션에서 등급이 gold인 튜플을 검색하시오
σ등급 ='gold'(고객) 또는 고객 where 등급='gold'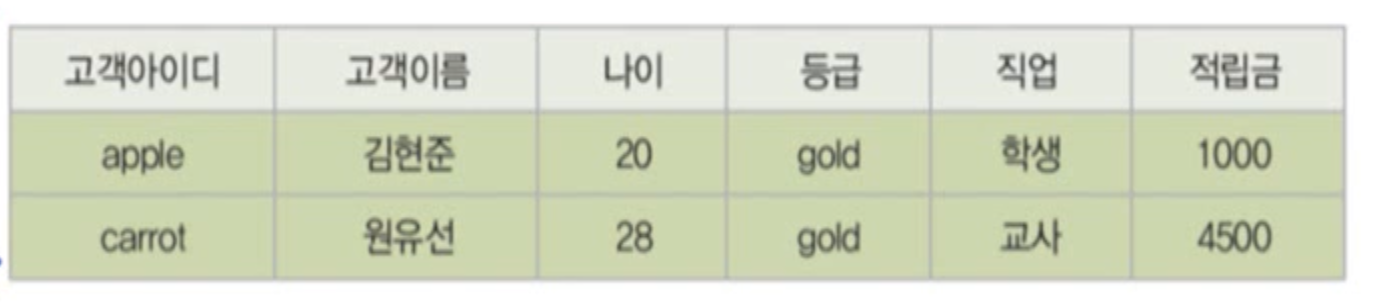
결과 릴레이션은 연산 대상 릴레이션의 수평적 부분 집합
-
고객릴레이션에서 등급이 gold이고, 적립금이 2000이상인 튜플을 검색하시오
σ등급 = 'gold' and 적립금>=2000 또는 고객 where 등급='gold' and 적립금 >= 2000
- 교환적 특징이 있음.
프로젝트(project)
- 릴레이션에서 선택한 속성의 값으로 결과릴레이션을 구성
- 하나의 릴레이션을 대상으로 연산을 수행
- 수학적 표현법 : π속성리스트(릴레이션)
- 데이터 언어적 표현법 : 릴레이션[속성리스트]
그림
- 고객릴레이션에서 고객이름, 등급, 적립금을 검색하시오
π고객이름,등급,적립금(고객) 또는 고객[고객이름,등급,적립금]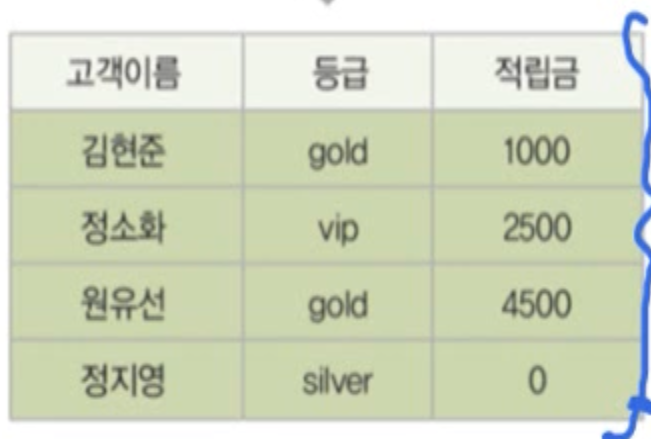
결과 릴레이션은 연산 대상 릴레이션의 수직적 부분 집합
-
고객릴레이션에서 등급을 검색하시오
등급(고객) 또는 고객[등급]
조인(join)
- 조인 속성을 이용해 두 릴레이션을 조합하여 결과릴레이션을 구성
- 조인속성은 값이 같은 튜플만 연결하여 생성된 튜플을 결과 릴레이션에 포함
- 조인 속성 : 두 릴레이션이 공통으로 가지고 있는 속성 - 표현법 : 릴레이션1 ⋈ 릴레이션2
- 자연 조인(natural join)이라고도함
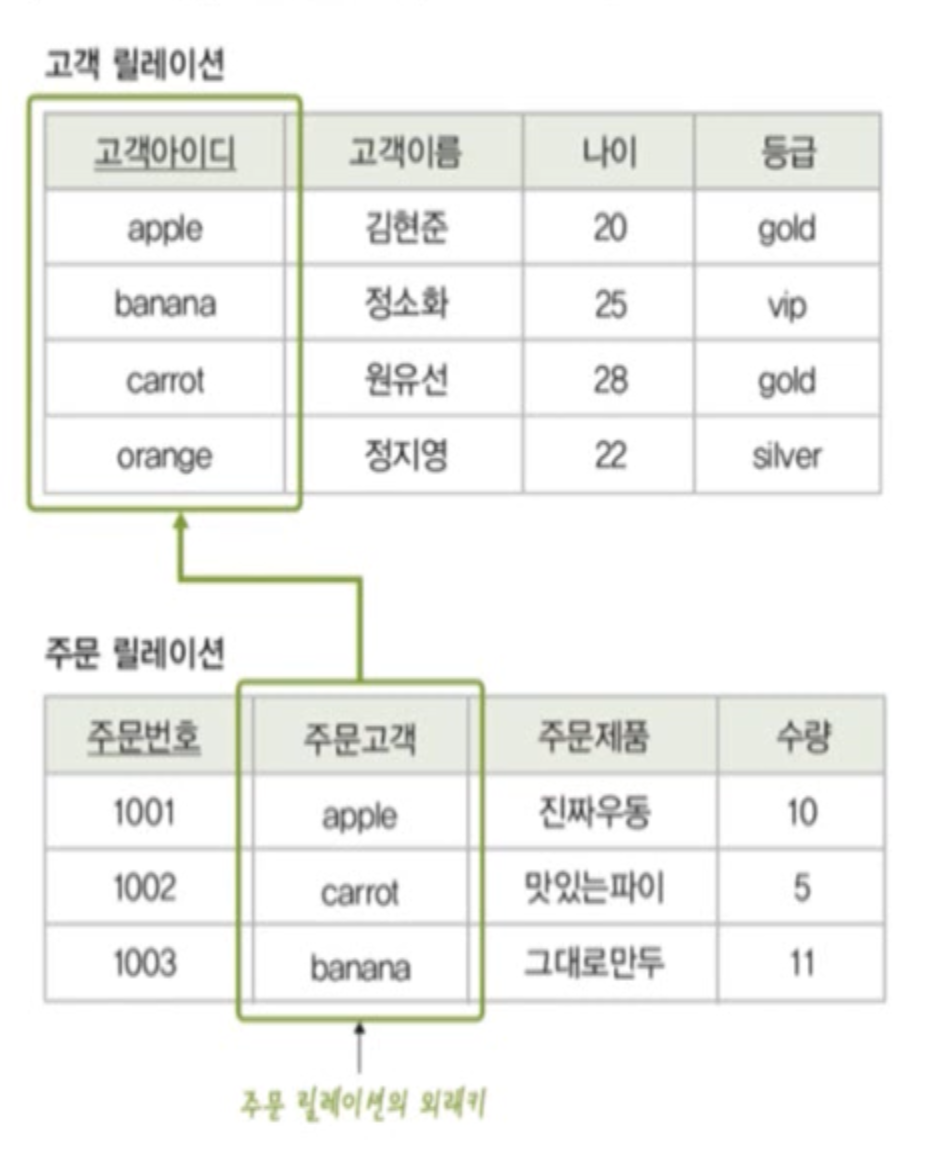
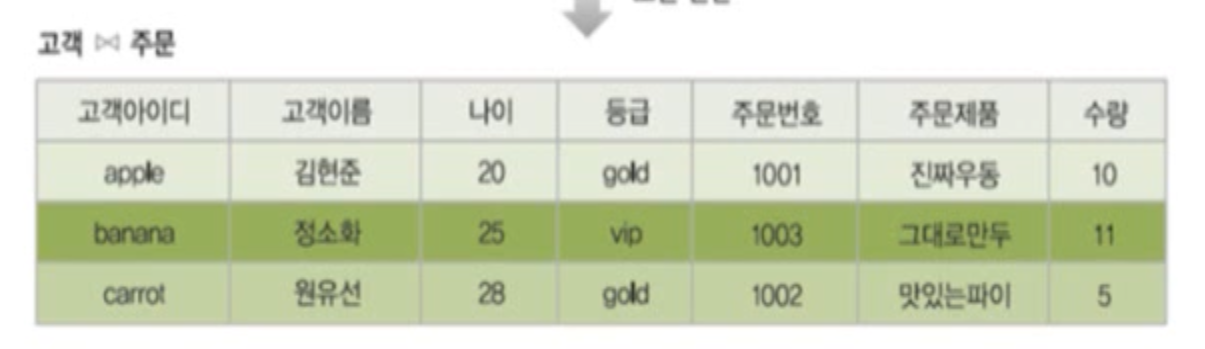
조인속성 : (고객)고객아이디, (주문)주문고객
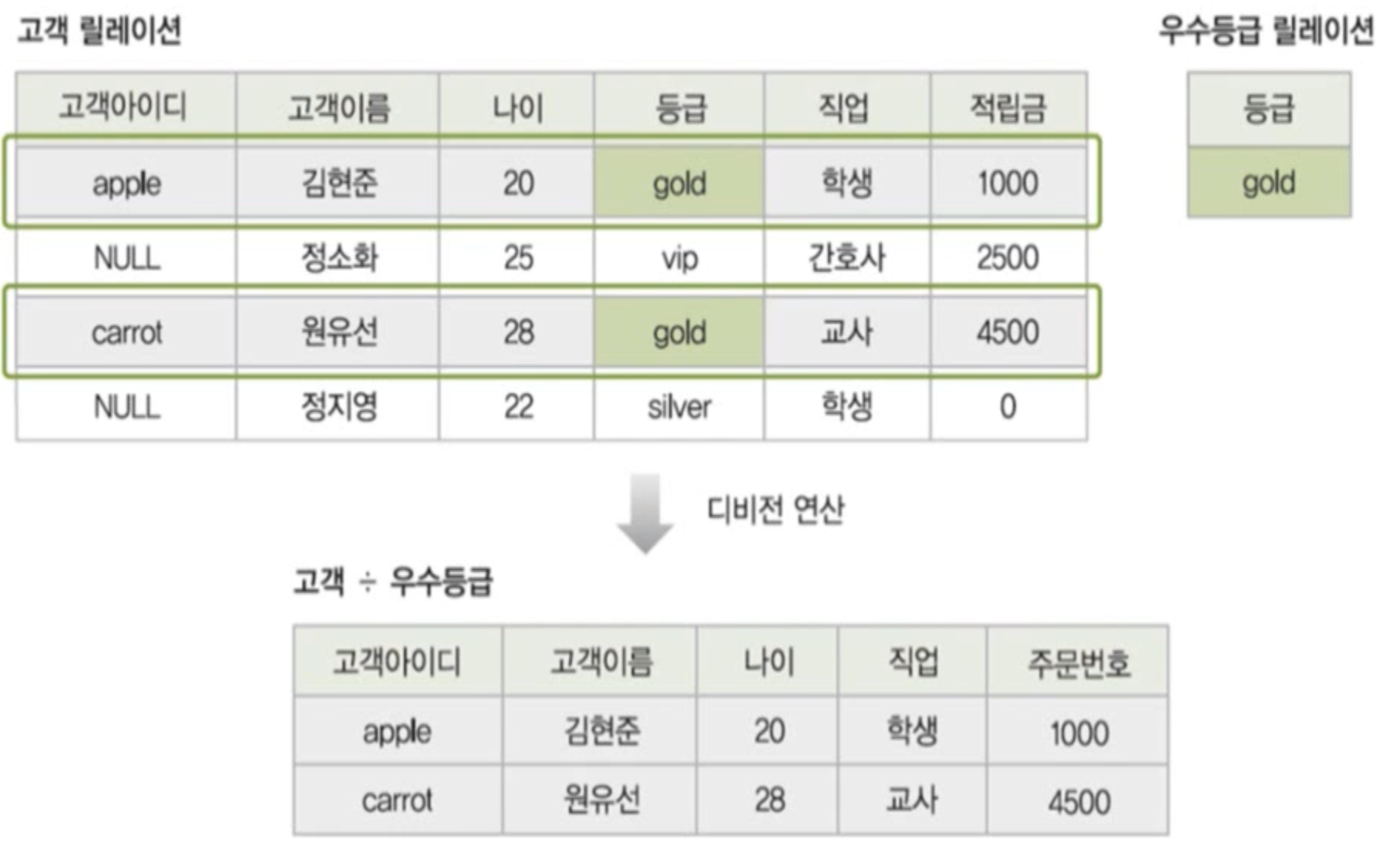
디비전(division)
- 표현법 : 릴레이션1 ÷ 릴레이션2
- 릴레이션2의 모든 튜플과 관련이 있는 릴레이션1의 튜플로 결과 릴레이션을 구성
- 단, 릴레이션1이 릴레이션2의 모든속성을 포함하고 있어야 연산이 가능함
그림
그림
관계 대수를 이용한 질의 표현 예
-
등급이 gold인 고객의 이름과 나이를 검색하시오
π이름,나이(σ등급='gold'(고객))
-
고객이름이 원유선인 고객의 등급과, 원유선 고객이 주문한 주문제품, 수량을 검색하시오.
π등급,주문제품,수량(σ고객이름='원유선'(고객⋈주문)) -
주문수량이 10개 미만인 주문 내역을 삭제하시오
주문-(σ주문수량<10(주문))
다음 세개의 릴레이션 스키마를 보고 각 물음에 답하시오.

1. π과목이름(과목)
2. π학번,이름(σ학년=1(학생))
3. π학번,과목번호,학점(σ중간성적>=80∧기말성적>=70(수강))
4. π학번,과목번호(수강)÷π과목번호(과목)
5. π이름,학년(σ과목번호=3∧학점='A0'(학생⋈수강))다음 네개의 릴레이션 스키마를 보고 각 물음에 답하시오

1. π번호,이름(σ수수료<5(판매자))
2. π판매자이름,수수료(σ고객번호='C001'∧제품번호='P003'(판매자⋈주문))
3. π이름(고객) - π이름(σ판매자번호='A003'(고객⋈주문))
4. π판매자번호,고객번호(주문)÷π고객번호(σ거주도시='부산'(고객))