알고리즘 복잡도

알고리즘 성능 분석이 필요한 이유

• 시간이 지날수록 데이터가 많아져, 처리해야 될 데이터도 방대해지고 있음
• 같은 결과를 내는 알고리즘이라도 효율성의 차이가 생김
• 알고리즘 수행 시작부터 결과 도출까지의 걸리는 시간이 짧고, 메모리와 같은 컴퓨터의 자원을 적게 사용하는 효율적인 알고리즘의 중요성이 대두되고 있음
• 같은 알고리즘이라도 하드웨어나 언어(컴파일 언어, 베이직 언어) 등의 차이에 따라 다른 효율을 보여주므로 반드시 같은 조건하에서 테스트를 해야함
• 알고리즘의 효율성을 나타낼 수 있는 시간복잡도(Time Complexity) 와 공간복잡도 (Space Complexity) 를 나타내는 표기법으로는 빅O (Big O notaion) 표기법이 있음

Big O 표기법 (Big O notation)

• 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수학적 방법
• 주로 두가지 방법을 통해서 도출해내는데

  1. 상수항 무시 : 입력값 n 이 상수항을 무시하기에 충분하다고 가정하기 때문에 상수항을 무시하고 표기

     ex) O(3N + 5) → O(N)

  2. 영향력 없는 항 무시 : 입력값 n 중에 가장 영향력이 큰 항을 제외한 나머지 항들은 무시함

     ex) O(n^2 + 3N + 5) → O(n^2)

공간복잡도 (Space Complexity)

• 작성한 프로그램이 얼마나 많은 공간(메모리)를 차지하느냐를 분석
• 현대에는 컴퓨터의 성능 발달로 메모리에 여유공간이 있어 시간복잡도가 더 중요하게 여겨지는 추세

num = 7

• 위와 같이 공간이 하나 생성되는 것은 공간복잡도 O(1)

for(i 0..10) {
	num += i
}

• 위와 같은 것도 i 와 num 변수만 for 문 안에서 사용하기 때문에 O(1) 의 공간복잡도를 가짐

fun fibo(num : Int) : Int {
	return fibo(num-2) + fibo(num-1)
}

• 위와 같이 재귀적으로 호출되는 경우 스택에 n 부터 1까지 모두 쌓이므로 O(n) 의 공간복잡도를 가짐
• 배열의 크기, 동적할당의 수, 재귀호출의 수가 공간복잡도에 영향을 미침

시간 복잡도 (Time Complexity)

• 특정 알고리즘이 어떤 문제를 해결하는데 걸리는 시간
• 최악의 경우의 수를 기준으로 생각하는데, 아무리 많은 시간이 걸려도 이 시간안에는 끝날 작업이라는 개념으로 최대한으로 많이 걸릴수 있는 시간을 기준으로 삼음

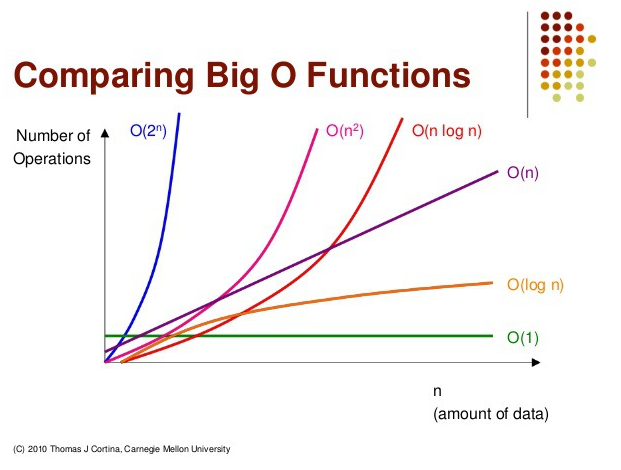
• O(1) (Constant)
  • 입력 데이터의 크기에 상관없이 일정한 시간이 걸리는 알고리즘
  • 데이터의 크기가 성능에 영향을 미치지 않음
• O(log n) (Logarithmic)
  • 입력 데이터의 크기가 커질수록 시간이 log 만큼 짧아지는 알고리즘
  • 데이터가 10배가 되면, 처리시간은 2배가 됨
• O(n) (Linear)
  • 입력 데이터의 크기에 비례해서 처리 시간이 증가
• O(n log n) (Linear - Logarithmic)
  • 데이터의 크기가 커질수록 처리시간이 log 배 만큼 증가
  • 데이터가 10배가 되면, 처리시간은 20배가 됨
• O(n^2) (quadratic)
  • 데이터의 크기가 커질수록 처리시간이 제곱만큼 증가
  • 데이터가 10배가 되면, 처리시간은 100배가 됨
  • 이중 for 문이 주로 해당, m 이 n 보다 작을 경우는 O(nm) 으로 표기
• O(2^n) (Exponential)
  • 데이터의 크기가 커질수록 처리시간이 기하급수적으로 증가
• 빅O 표기법에 사용되는 그래프로 곡선이 가파를수록 효율성이 떨어진다
  • O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^n) 순서
• 알고리즘은 주로 최악의 경우를 가정하고 빅 O 표기법을 사용

빅 O 표기법의 예제

• O(1) : 스택의 Push, Pop
• O(log n) : 이진트리
• O(n) : for 문
• O(n log n ) : 퀵 정렬 (quick sort), 병합정렬 (merge sort), 힙 정렬(heap sort)
• O(n^2) : 이중 for 문, 삽입정렬(insert sort), 버블정렬(bubble sort), 선택정렬(selection sort)
• O(2^n) : 피보나치 수열

시간복잡도를 줄이는 법

• 반복문이 시간복잡도에 가장 큰 영향을 끼치므로 반복문의 숫자를 줄이는 것이 중요
• 예를 들어 for 문이 O(n) 의 시간이 걸린다면, 이중 for 문은 O(n^2) 의 시간이 걸림
• 자료구조를 상황에 따라서 적절하게 활용하는 것도 좋은 방법

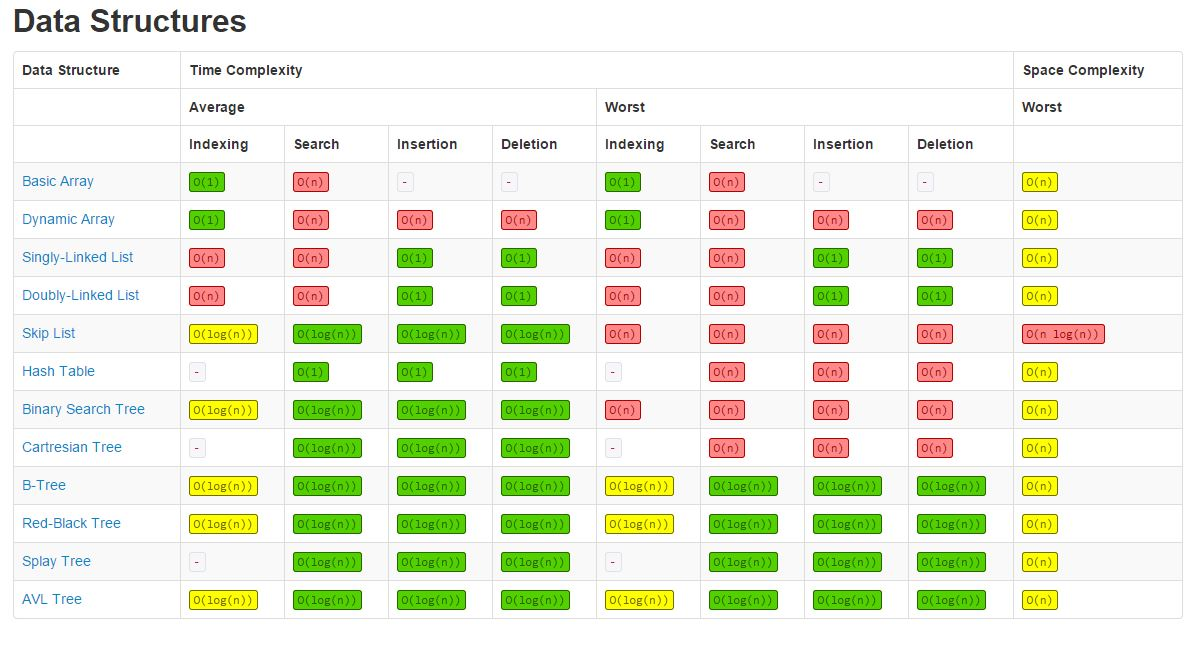
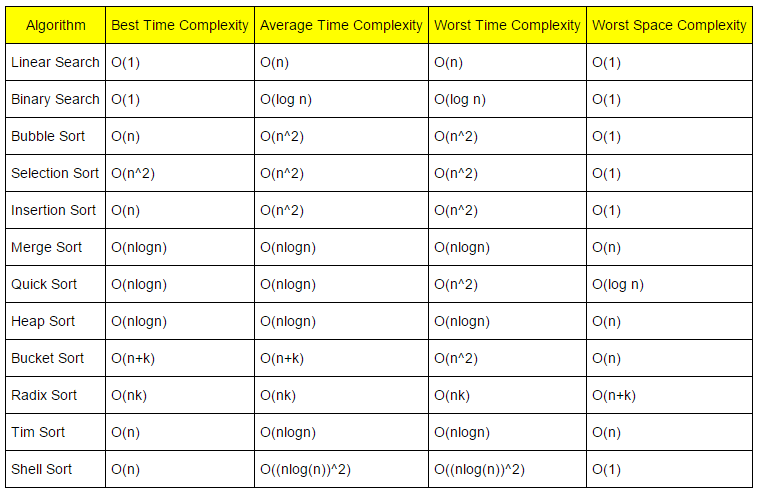
• 아래 표와 같이 각 알고리즘마다 시간 복잡도가 다르기때문에 상황에 맞게 적절하게 활용하여야 한다.

Reference
Pictures From.
https://www.hackerearth.com/practice/notes/big-o-cheatsheet-series-data-structures-and-algorithms-with-thier-complexities-1/