PyTorch Lecture 02: Linear Model

조병근·2020년 9월 12일

PyTorch Lecture

목록 보기

2/4

Sung Kim 교수님의 ML / DL for Everyone with PYTORCH 강의 필기내용입니다.

저번 강의에서 봤던 위와 같은 경우처럼 dataset을 정답과 함께 제공하는 학습 방식을 지도학습(Supervised Learning) 이라고 한다.

Model design

Model은 입력값 x를 받아 예측값 y^(y hat)을 내 놓는다.

좋은 Model을 설계하기 위해서 입력값과 결과값의 관계를 알아야 하는데,

위의 경우는 Linear relationship을 가지고 있다. Linear relationship을 가지고 있다는 말은 두 데이터 값 사이에 직선식의 형태가 있다는 말이다.

Linear Regression

❓ 선형회귀(Linear Regression)

종속변수 y와 독립변수 x 사이의 선형 상관 관계를 모델링하는 회귀분석 기법이다.
데이터들을 가장 잘 설명할 수 있는 선을 찾는 것이다.

입력값 x, w ( weight ), b ( bias ) 를 이용해 예측값 y^을 구한다. 이게 Model이다. bias b는 생략할 수 있다.

🤔 Linear Regression error ?

파란색 선이 training data를 이용해 그은 True line이다. w에 랜덤값을 넣어가며 예측을 하는데, True line과의 차이가 가장 적게 나는 w를 구하는 게 목표다.

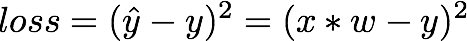
주어진 data point에서의 예측값과 실제값의 차이를 구하면 오차값을 구할 수 있다. 그 오차를 loss라고 한다. 즉 lose가 최소인 w를 찾으려고 시도할 것이고 그 과정을 Learning이라고 한다.

예시로 w=4일 때 예측값과 Loss를 나타내는 표이다. Loss들을 대표하는 값으로 평균값을 사용했다. 다른 값들을 넣어가며 mean값이 가장 작은 경우를 찾아야 한다.

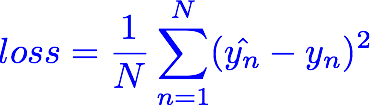
loss(MSE)가 최소가 될 때는 w=2일 때다.

❓ MSE(mean square error)

오차의 제곱에 대한 평균

Loss graph :

🚀 Let's do it

Model & Loss

# Model
def forward(x):
    return x * w

# Loss
def loss(x,y):
    y_pred=forward(x)
    return (y - y_pred) * (y - y_pred)

Compute loss for w

# Compute loss for w
for w in np.arange(0.0, 4.1, 0.1):
    print ("[*] w="+str(w))
    l_sum = 0
    for x_val, y_val in zip(x_data,y_data): # zip(x_data,y_data) -> (1.0,2.0) , (2.0,4.0) , (3.0,6.0)
        y_pred_val=forward(x_val)
        l = loss(x_val,y_val)
        l_sum += l
        mse = l_sum/3
        print ("\t", x_val, y_val ,y_pred_val, l)
    print ("[*] MSE="+str(mse))

Plot graph


for w in np.arange(0.0, 4.1, 0.1):
    print ("[*] w="+str(w))
    l_sum = 0
    for x_val, y_val in zip(x_data,y_data): # zip(x_data,y_data) -> (1.0,2.0) , (2.0,4.0) , (3.0,6.0)
        y_pred_val=forward(x_val)
        l = loss(x_val,y_val)
        l_sum += l
        mse = l_sum/3
        print ("\t", x_val, y_val ,y_pred_val, l)
    print ("[*] MSE="+str(mse))
# Plot graph
    w_list.append(w)
    mse_list.append(mse)
    
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

🏁 Exercise.py

import numpy as np
import matplotlib.pyplot as plt
w = 1.0 # a random guess
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w_list = []
mse_list = []

# Model
def forward(x):
    return x * w

# Loss
def loss(x,y):
    y_pred=forward(x)
    return (y - y_pred) * (y - y_pred)

# Compute loss for w
for w in np.arange(0.0, 4.1, 0.1):
    print ("[*] w="+str(w))
    l_sum = 0
    for x_val, y_val in zip(x_data,y_data): # zip(x_data,y_data) -> (1.0,2.0) , (2.0,4.0) , (3.0,6.0)
        y_pred_val=forward(x_val)
        l = loss(x_val,y_val)
        l_sum += l
        mse = l_sum/3
        print ("\t", x_val, y_val ,y_pred_val, l)
    print ("[*] MSE="+str(mse))
    # Plot graph
    w_list.append(w)
    mse_list.append(mse)
    
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()