Sung Kim 교수님의 ML / DL for Everyone with PYTORCH 강의 필기내용입니다.
저번 강의에서 Gradient를 이용해 loss(w)가 최소인 값을 찾았다. 그러기 위해서 직접 Gradient를 구해줬는데, 신경망이 복잡해지면 Gradient를 계산하는 게 어려워지고 심지어는 불가능해진다. 이를 해결하기 위한 방법을 배워보자.
Computational graph + chain rule
chain rule
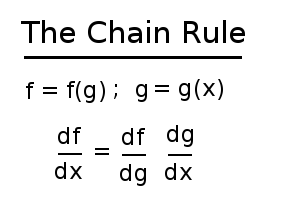
EX:

x,y 를 입력으로 받아 z를 만들어 낸다. 이런 노드들이 여러 개 연결되어, 최종적으로는 LOSS를 구한다. 우리의 목표는 dLOSS/dx, dLOSS/dy를 구하는 것이다.
Forward pass - x, y를 이용해 z를 구한다.
Backward propagation
0. dz/dx, dz/dy를 구한다.
1. dLOSS/dz를 이 다음 노드로부터 구할 수 있다.
2. 그를 이용해서 dLOSS/dx(=dLOSS/dz * dz/dx),dLOSS/dy를 구한다.
Computational graph
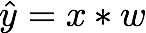
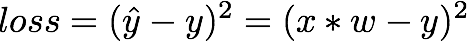
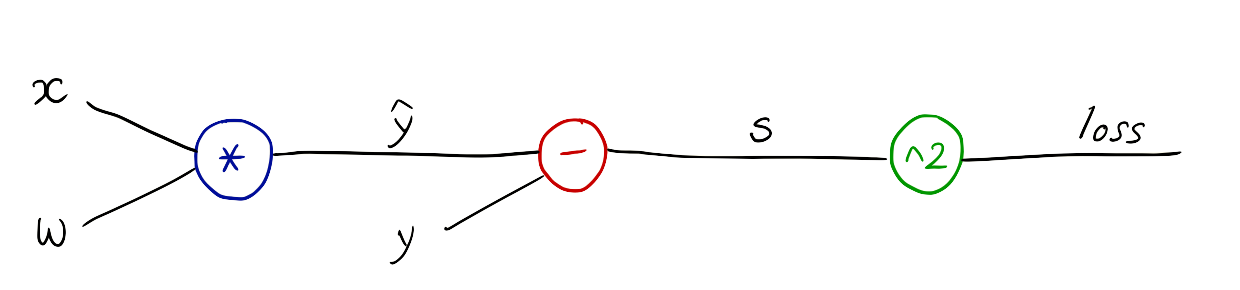
우리가 짠 모델에 대해서 Computational graph를 그려보면 위와 같다.
-
Forward pass : x, y, w에 값을 대입해 s, loss를 구한다.
-
Backward propagation:
- 각각의 gate에서 local gradient를 구한다.
-dloss/ds를 구한다. ➜ 이걸 이용해서dloss/dy^을 구한다.
- 각각의 gate에서 local gradient를 구한다.
Exercise
🚀 Exercise.py
import torch
from torch.autograd import Variable
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
# Model
def model(x):
return x * w
# Loss
def loss(y_pred,y):
return (y - y_pred) * (y - y_pred)
# Forward pass
w=Variable(torch.Tensor([1.0]), requires_grad=True)
for epoch in range(100):
for x_val, y_val in zip(x_data,y_data):
y_pred=model(x_val)
l = loss(y_pred,y_val)
l.backward()
print ("\tgrad:",x_val,y_val,w.grad.item())
w.data=w.data - 0.01 * w.grad.item()
# w.grad = dloss/dw
w.grad.data.zero_()
print ("Epoch : {} | Loss : {}".format(epoch,l.item()))
print ("[*]predict (after training)",4,model(4).item())모르는 게 좀 나온 거 같아서 공부해봤다.
w=Variable(torch.Tensor([1.0]), requires_grad=True)Variable은 Tensor의 Wrapper이고, computational graph에서 node로 표현된다. w가 Variable일 때 w.data는 그 값을 갖는 Tensor이고, w.grad는 gradient를 갖고 있는 또 다른 Variable이다.
requires_grad=True는 backward propagation 중에 이 Variable에 대한 gradient를 계산할 필요가 있음을 나타낸다.
Forward Pass
w=Variable(torch.Tensor([1.0]), requires_grad=True)
...
y_pred=model(x_val)
l = loss(y_pred,y_val)Backward propagation
l.backward()backward propagation을 진행하면서 computational graph Variable들의 gradient를 저장한다.
TODO
Numpy 로만 구현
