백준 1041 주사위

jathazp·2021년 8월 16일

구현 백트래킹

algorithm

목록 보기

49/57

문제링크

https://www.acmicpc.net/problem/1041

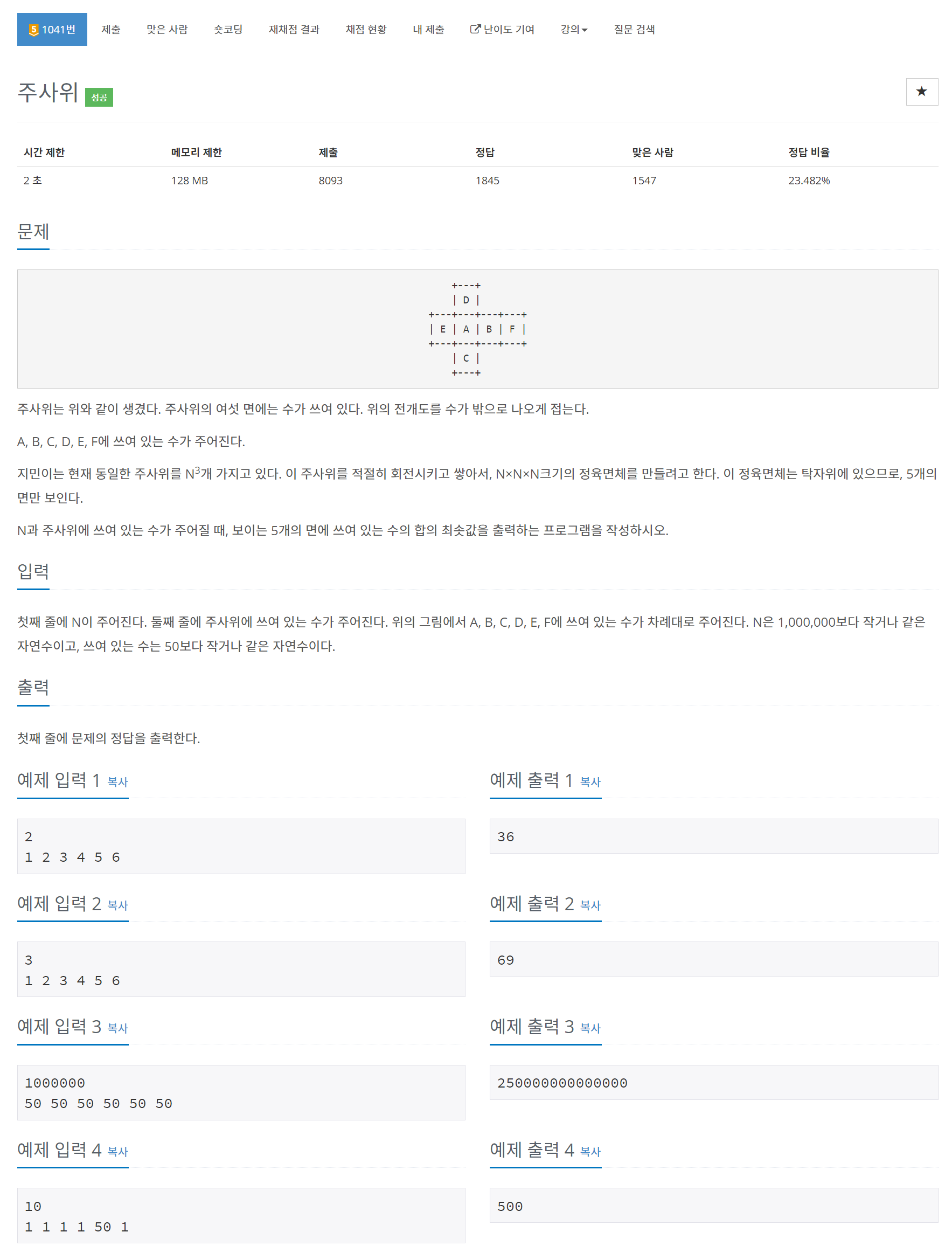
문제

풀이

백트래킹을 이용해 조합을 구해주었다.
그리고 해당 조합에서 최소의 값을 갖는 경우를 반환해 주었다.

주사위에서 1개의 면만 보일때 최소의 값
=> 6C1 을 탐색하며 최소의 값을 반환

주사위에서 2개의 면만 보일때 최소의 값
=> 6C2 를 탐색하며 최소의 값을 반환.
단, 뽑아낸 주사위의 두 면에서 두 면이 마주보는 경우가 있으면 동시에 보일 수 없으므로 예외처리

주사위에서 3개의 면만 보일때 최소의 값
=> 6C3 를 탐색하며 최소의 값을 반환.
단, 뽑아낸 주사위의 세 면 중 두 면이 마주보는 경우가 있으면 동시에 보일 수 없으므로 예외처리

뽑아낸 면은 vi 배열을 통해 체크해주었다.

코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>
using namespace std;
#define MAX_NUM 250000000000001
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5

typedef long long ll;

ll n;
vector<ll> arr;
bool vi[6];

ll select(int cnt, ll sumn, int idx, int type) {
	if (type == 1 && cnt == 1) {
		return sumn;
	}
	else  if (type == 2 && cnt == 2 || type == 3 && cnt == 3) {
		if (vi[A] && vi[F] || vi[B] && vi[E] || vi[C] && vi[D]) return MAX_NUM;
		return sumn;
	}
	if (idx >= 6) return MAX_NUM;


	ll temp = MAX_NUM;
	vi[idx] = true;
	temp = min(temp, select(cnt + 1, sumn + arr[idx], idx + 1, type));
	vi[idx] = false;
	temp = min(temp, select(cnt, sumn, idx + 1, type));

	return temp;
}


int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);


	cin >> n;
	for (int i = 0; i < 6; i++) {
		ll num; cin >> num;
		arr.push_back(num);
	}

	ll one = select(0, 0, 0, 1);
	ll two = select(0, 0, 0, 2);
	ll three = select(0, 0, 0, 3);

	if (n == 1) cout << accumulate(arr.begin(), arr.end(), 0) - *max_element(arr.begin(), arr.end());
	else cout << (n - 2) * (n - 1) * 4 * one + (n - 1) * 4 * two + (n - 2) * (n - 2) * one + (n - 2) * 4 * two + 4 * three;

}