백준 2650 교차점 개수

문제링크

https://www.acmicpc.net/problem/2650

---

문제

---

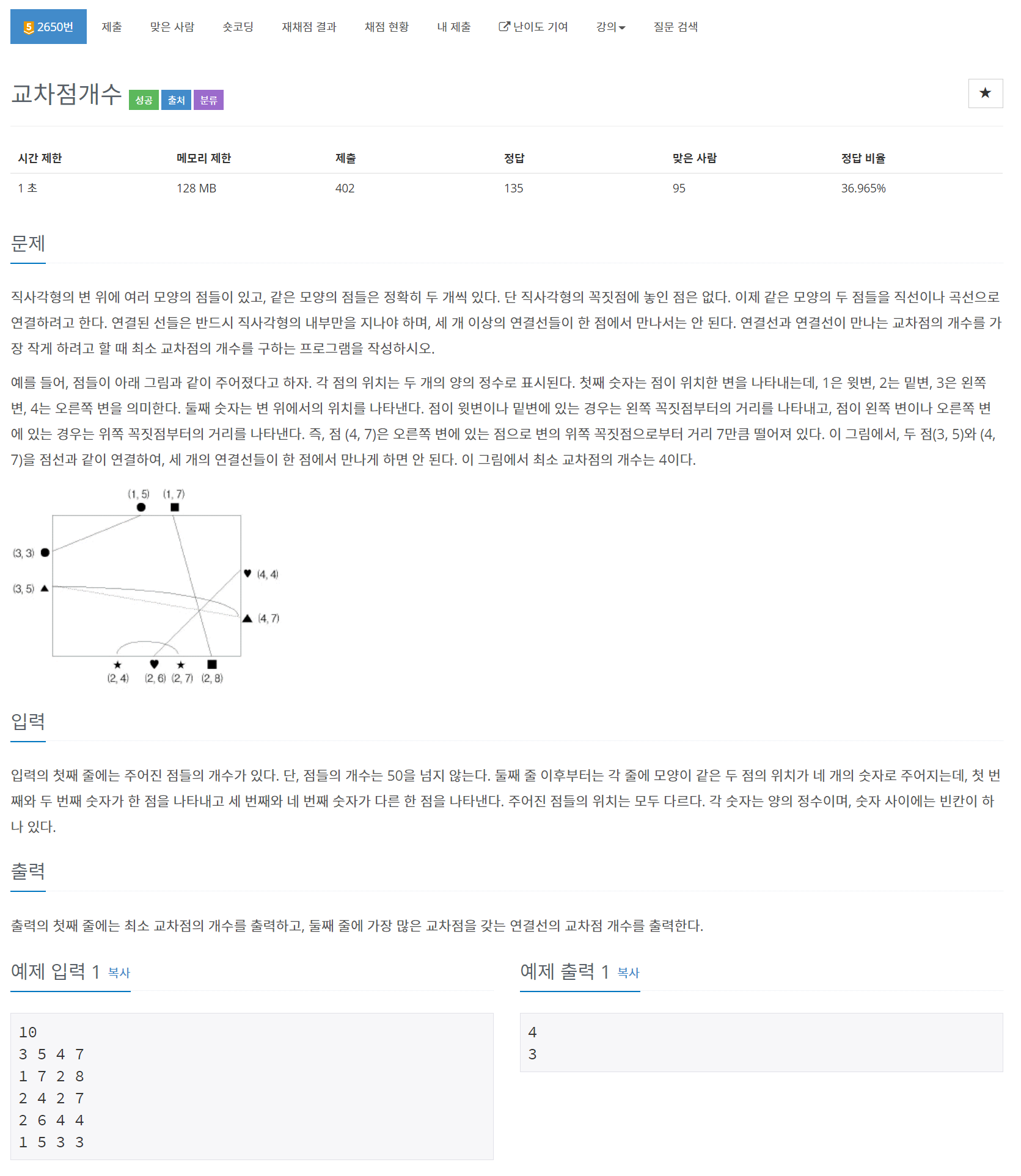
풀이

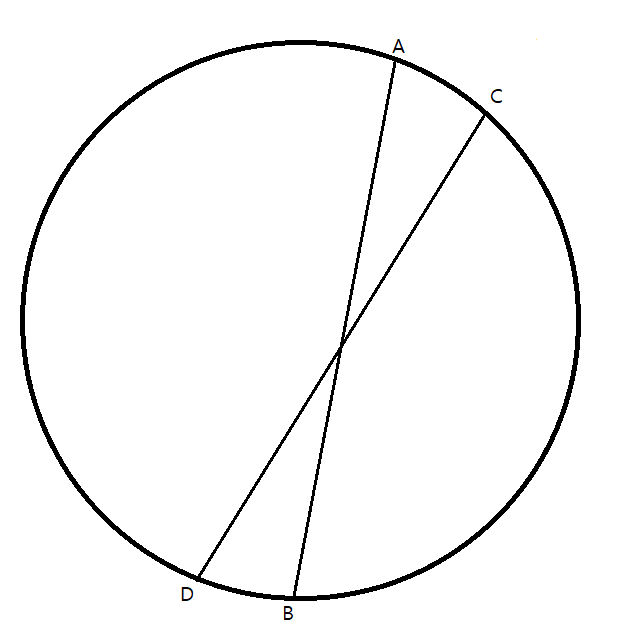
점이 최대 50개 이므로 O(N^2)의 풀이로 풀어주었습니다.

1. 사각형을 원으로 치환해주었습니다.

2. 점의 각 좌표는 원의 한 기준점에서 해당 좌표까지의 거리로 치환해주었습니다.

3. 이렇게 바꿔주었을 때 선분 ab를 기준으로 if(a<c && c<b && b<d) 인 경우 선분이 교차한다고 판단하고 풀어주었습니다.

---

시행착오

처음에 CCW알고리즘을 이용해 교차여부를 판단하려 하였으나 8% 에서 계속 오류가 나는것을 못잡고 새로 풀었습니다.
CCW를 이용한 풀이도 가능할것 같으니 다음에 다시 풀어봐야겠습니다.

---

코드

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
#define MUL 10000000
int trans(int a,int b) {
	if (a == 1) return b;
	else if (a == 2) return MUL * 2 + MUL - b;
	else if (a == 3) return MUL * 3 + MUL - b;
	else if (a == 4) return MUL + b;
}
int main() {
	int n;
	cin >> n;

	vector<pair<int, int>> v;
	for (int i = 0; i < n/2; i++) {
		int a,b,c,d;
		cin >> a >> b >> c >> d;
		int p1 = trans(a,b);
		int p2 = trans(c,d);
		if (p1 > p2) swap(p1, p2);
		v.push_back({ p1, p2 });
	}

	int ans = 0, maxn = 0;
	for (int i = 0; i < v.size(); i++) {
		int temp = 0;
		for (int j = 0; j < v.size(); j++) {
			if (i == j) continue;
			pair<int, int> line1 = v[i];
			pair<int, int> line2 = v[j];
			if (line1.first > line2.first) swap(line1, line2);
			if (line1.first < line2.first && line2.first < line1.second && line1.second < line2.second) temp++;
		}
		maxn = max(maxn, temp);
		ans += temp;
	}
	cout << ans/2 << '\n' << maxn;
}

---

후기

https://gaussian37.github.io/math-algorithm-line_intersection/
https://jason9319.tistory.com/358
해당 블로그에 ccw알고리즘에 대한 설명이 잘되어 있으니 다음에 다시 공부해봐야겠네요.