백준 2887 행성터널

문제링크

https://www.acmicpc.net/problem/2887

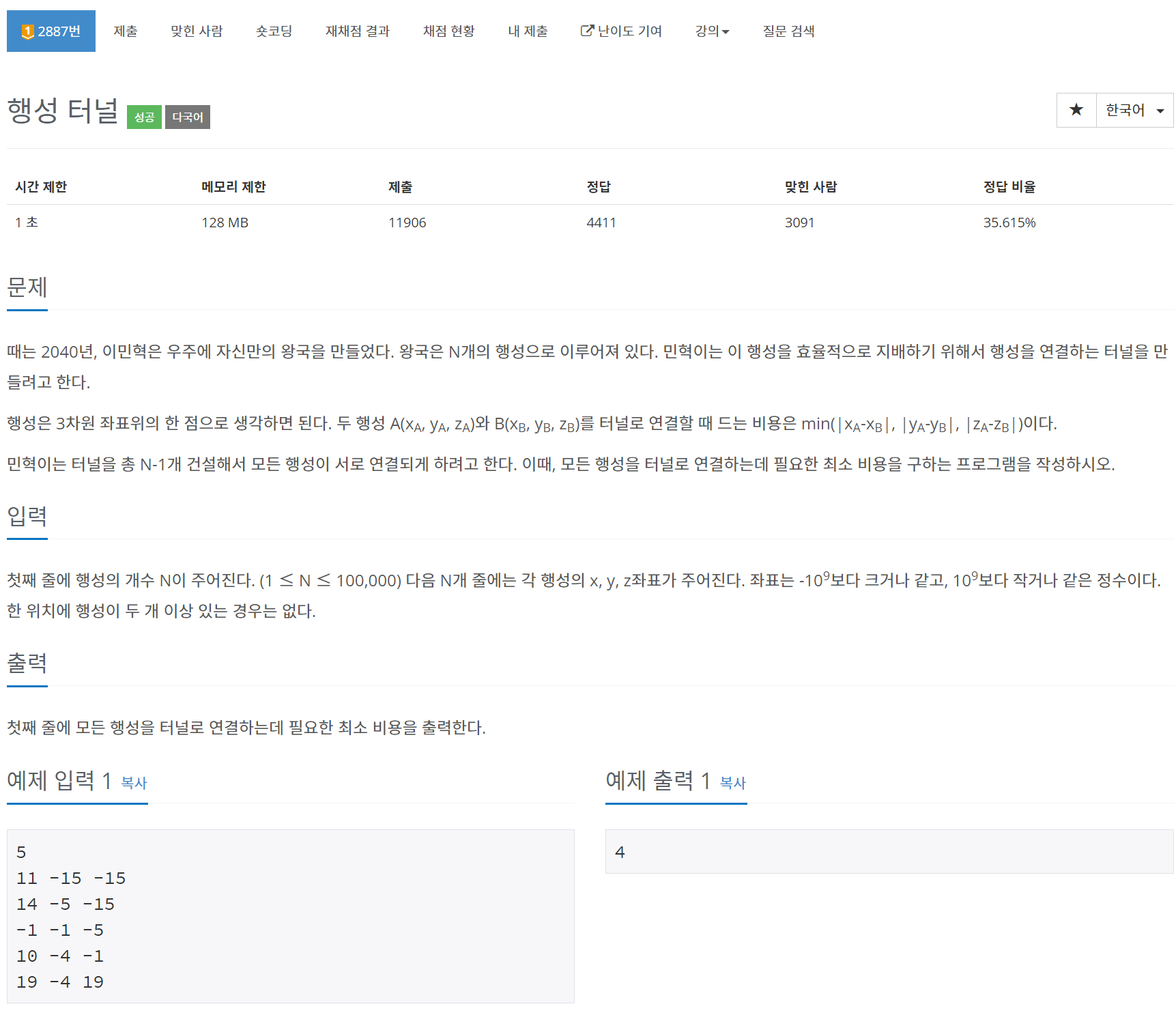
문제

풀이

어차피 두 행성간 거리는 min(Xa-Xb,Ya-Yb,Za-Zb) 이기 때문에
먼저 정렬 시킨 후 인접한 점들만 비교해주면 된다.

따라서 x y z 값들을 각각 x벡터, y벡터, z벡터에 나눠담고
각 벡터를 정렬시켜주었다.

그 후에 인접한 값들의 차(거리)를 d벡터에 담아주었다.
=> d벡터에는 각 행성의 번호와 거리가 저장된다.

마지막으로 d벡터에 대해 거리 기준으로 오름차순 정렬을 시키고 크루스칼 알고리즘을 적용시켜 문제를 해결했다.

코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int parents[100001];
int find_parent(int x) {
	if (x == parents[x]) return x;
	else return parents[x] = find_parent(parents[x]);
}

typedef struct dist {
	int dist;
	int from, to;
}dist;

bool cmp(pair<int,int> a,pair<int,int> b){
	return a.first > b.first;
}

bool cmp2(dist a, dist b) {
	return a.dist < b.dist;
}


int main() {
	vector<pair<int, int>> xv,yv,zv;
	vector<dist> d;
	int n,ans=0;
	cin >> n;

	for (int i = 0; i < n; i++) {
		parents[i] = i;
	}//init

	for (int i = 0; i < n; i++) {
		int x, y, z;
		cin >> x >> y >> z;

		xv.push_back({ x,i });
		yv.push_back({ y,i });
		zv.push_back({ z,i });
	}

	sort(xv.begin(), xv.end(),cmp);
	sort(yv.begin(), yv.end(),cmp);
	sort(zv.begin(), zv.end(),cmp);

	for (int i = 0; i < xv.size()-1; i++) {
		d.push_back({ xv[i].first - xv[i + 1].first,xv[i].second,xv[i + 1].second });
	}

	for (int i = 0; i < yv.size()-1; i++) {
		d.push_back({ yv[i].first - yv[i + 1].first,yv[i].second,yv[i + 1].second });
	}

	for (int i = 0; i < zv.size()-1; i++) {
		d.push_back({ zv[i].first - zv[i + 1].first,zv[i].second,zv[i + 1].second });
	}

	sort(d.begin(), d.end(),cmp2);
	
	for (int i = 0; i < d.size(); i++) {
		int p1 = find_parent(d[i].from);
		int p2 = find_parent(d[i].to);

		if (p1 != p2) {
			parents[p1] = p2;
			ans += d[i].dist;
		}
	}

	cout << ans;
}

후기

1<=N<=100000이기 때문에 모든 행성간의 거리를 직접 구해서 크루스칼 알고리즘을 적용시키는데는 무리가 있다.

인접한 값들만 비교하면 된다는 아이디어가 핵심