자료구조와 알고리즘

자료구조와 알고리즘을 공부하면 기초 코딩 능력 뿐만 아니라 논리적 사고와 전산화 능력, 엣지 케이스 탐색 등의 문제 해결 능력도 기를 수 있다.

자료구조란

자료구조란 메모리를 효율적으로 사용하며 빠르고 안정적으로 데이터를 처리하는 것이 궁극적인 목표이다. 자료구조는 특정 상황에 따라 유용할 수 있도록 특정 구조를 이루고 있다. 이 말은 상황에 맞지 않은 자료구조를 사용한다면 비효율적이 될 수 있으므로 상황에 알맞는 자료구조를 이용할 수 있어야 한다.

자료구조의 종류

단순구조	선형구조	비선형구조
정수	배열	트리
실수	연결리스트	그래프
문자열	스택
논리	큐

알고리즘이란

알고리즘이란 특정 문제를 효율적으로 빠르게 해결하는 것이 궁극적인 목표이다. 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것이다.

시간복잡도

빅오표기법(Big-O notation)

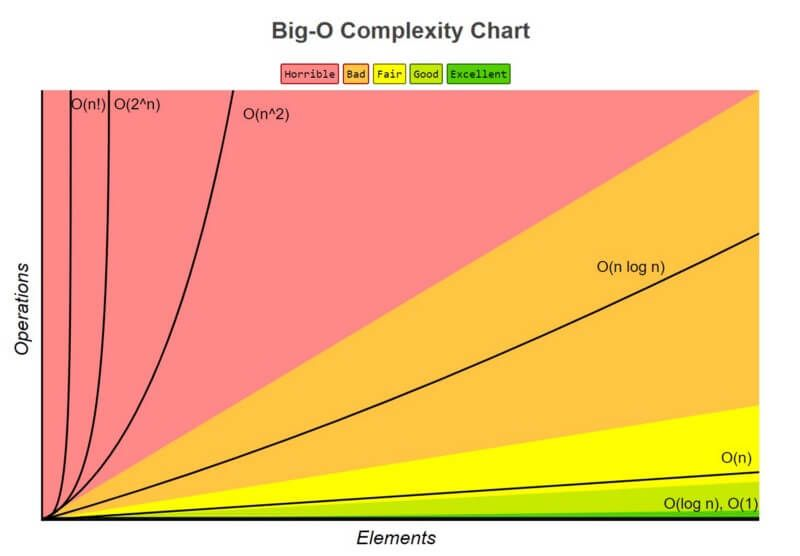
빅오표기법은 알고리즘의 성능과 복잡도를 간단한 기호로 표시하는 시간복잡도의 표기법 중 하나이다. 입력인 $n$이 커질수록 알고리즘이 얼마나 효율적인지 표현하는 방식이다. 즉, 정확도가 아닌 점진적인 추세를 나타낸다.

빅오표기법에서 위의 그림을 참고하여 가장 빠른 순부터 나열하면 다음과 같다.

$O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)$

$O(1)$

상수 시간은 대상이나 조건에 상관없이 항상 일정한 성능, 실행시간을 갖는 것이다.

예를 들면, 다음과 같은 함수가 있을 때 인자에 상관없이 언제나 연산이 항상 3개 이다.

function add(n) {
    return n * (n + 1) / 2;
}

이런 경우에 시간이 상수가 되므로 시간 복잡도는 $O(1)$이 된다.

$O(\log n)$

로그시간은 $n$에 로그를 씌운만큼 시간이 줄어든다. 숫자 $n$이 1보다 작아지기 전에 2로 나누어지는 횟수이다.빅오표기법에서 사용하는 $\log n$는 $\log_{2}n$이다. 따라서 다음과 같은 예시가 있다.

for (let i = n; i >= 1; i /= 2) {
	// 연산
}

// * * * OR * * * //

for (let i = 1; i < n; i *= 2) {
	// 연산
}

$O(n)$

선형시간은 $n$이 커질수록 1:1 비율로 시간이 증가한다. 예를 들어 배열을 순회할 때, 배열의 길이가 1이면 1만큼의 비용이 발생하고, 배열의 길이가 10이면 10, 100이면 100만큼의 비용이 발생한다. 즉, 선형으로 비용이 발생한다.

for (let i = 0; i < n; i++) {
	// 연산
}

연산의 갯수는 $n$의 곱과 궁극적으로 연결되어 있으며, $1n$, $10n$, $100000n$, ... 등에 상관없이 $O(n)$이 된다.

for (let i = 0; i < n; i++) {
	// 연산
}

for (let i = n; i > 0; i--) {
	// 연산
}

따라서 위의 예시도 $2n$의 시간을 갖지만 $O(n)$로 나타낸다.

for (let i = 0; i < Math.max(5, n); i++) {
	// 연산
}

이 경우에는 어떻게 될까?
i가 5까지는 항상 연산을 5번만 실행할 것이다. 그러나 시간복잡도는 $n$의 값이 커질수록 시간 비용을 측정하므로 이 경우에도 $n$이 5보다 충분히 커지게 되면 궁극적으로는 $O(n)$의 시간복잡도를 갖게 된다.

$O(n\log n)$

이 시간복잡도는 $O(n * log n) = O(n\log n)$으로 볼 수 있기 때문에 다음과 같은 예시로 들 수 있다.

for (let i = 0; i < n; i++) { // O(n)
	for (let j = 1; j < n; j *= 2) { // O(logn)
		// 연산
	}
}

$O(n^2)$

이차시간은 다음과 같이 중첩된 루프에서 나타난다.

for (let i = 0; i < n; i++) { // O(n)
	for (let j = 0; j < n; j++) { // O(n)
		// 연산
	}
}

시간복잡도는 곱하거나 더해질 수 있으므로 위의 예시처럼 최종 시간복잡도는 $O(n * n) = O(n^2)$이 된다. $O(n^2 + 100n + 8)$인 경우에도 가장 큰 차수를 따라 $O(n^2)$으로 나타낸다.

자료구조별 시간복잡도

자료구조	평균적인 경우	최악의 경우
	삽입	삭제	검색	삽입	삭제	검색
배열/스택/큐	O(1)	O(1)	O(n)	O(1)	O(1)	O(n)
연결 리스트	O(1)	O(1)	O(n)	O(1)	O(1)	O(n)
이중 연결 리스트	O(1)	O(1)	O(n)	O(1)	O(1)	O(n)
해시 테이블	O(1)	O(1)	O(1)	O(n)	O(n)	O(n)
이진 검색 트리	O(log(n))	O(log(n))	O(log(n))	O(n)	O(n)	O(n)

(미리보기로는 테이블이 정상적으로 보이는데 글을 발행하면 테이블이 이상해지네요;; 평균적인 경우, 최악의 경우 각각 삽입, 삭제, 검색 시 시간 복잡도를 나타낸 테이블 입니다.)

공간복잡도

공간복잡도란, 시간복잡도가 시간을 측정했다면 입력값에 상관없이 알고리즘이 사용되는 메모리에 주목하는 것이다.

자바스크립트에서 공간복잡도

대부분 원시 타입(boolean, number, undefined, null, ...)은 모두 불변 공간이다. 대부분이라고 한 이유는, 문자타입은 문자열 길이가 $n$이라면 $O(n)$의 공간이 필요하다.

참조 타입은 일반적으로 $O(n)$의 공간이 필요하다. $n$은 배열의 길이일 수도, 객체 키의 개수일 수도 있다.

예를 들어, 다음과 같은 함수가 있다고 하자.

function sum(arr) {
	let total = 0;
  	for (let i = 0; i < arr.length; i++) {
      	total += arr[i];
    }
  	return total;
}

입력값(인수)인 배열 arr에 상관 없이 사용되는 공간은 변수 total과 i 밖에 없다. 배열의 길이에 따라 변수가 추가되거나 그런 상황은 발생하지 않는다. 두 변수의 타입은 number이기 때문에 상수 공간, $O(1)$을 차지한다고 볼 수 있다.

function map(arr) {
	let newArr = [];
  	for (let i = 0; i < arr.length; i++) {
      	newArr.push(arr[i] * 2);
    }
  	return newArr;
}

이 경우에 알고리즘이 차지하는 공간은 새로운 배열이 입력된 배열의 길이에 비례해서 커지게 된다. 따라서 $O(n)$ 공간을 차지하게 된다.