DFS Depth First Search
깊이 우선 탐색
BFS Breadth First Search
너비 우선 탐색
필요 지식
Stack(스택)
Queue(큐)
Recursive(재귀)
스택과 재귀 학습
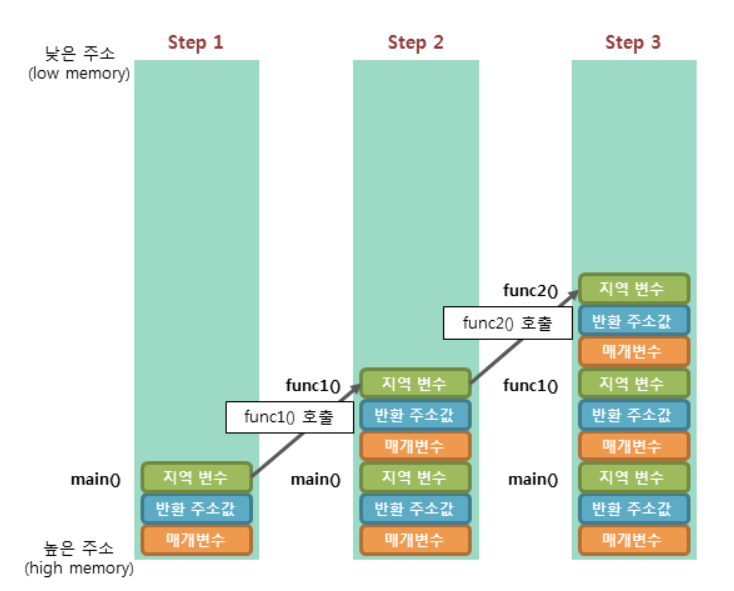
Stack Frame(스택 프레임)
정의
-
메모의 스택(stack) 영역은 함수의 호출과 관계되는 지역 변수와 매개 변수가 저장되는 영역이다.
-
스택 영역은 함수의 호출과 함께 할당되며, 함수의 호출이 완료되면 소멸한다.
-
함수가 호출되면 스택에는 함수의 매개변수, 호출이 끝난 뒤 돌아갈 반환 주소 값, 함수에서 선언된 지역변수 등이 저장된다.
-
이렇게 스택 영역에 차례대로 저장되는 함수의 호출 정보를 스택 프레임(stack frame)이라 한다.
-
스택 프레임을 활용하면 함수의 호출이 모두 끝난 뒤에 해당 함수가 호출되기 이전 상태로 되돌아 갈 수 있다.
재귀 함수
public class Recursive{
public static void main(String[] args){
Recursive T = new Recursive();
T.DFS(3);
}
public void DFS(int n) {
if(n==0){
return;
} else{
System.out.print(n + " ");
DFS(n-1);
}
}
}결과
- 3 2 1
설명
DFS 함수로 인자 값 3이 들어온다.
반복문을 돌듯 인자 값이 0 이 될 때 까지 같은 DFS 함수를 계속 호출함.
만약 1부터 오름차순으로 표출하려면 어떻게 해아할까?
public class Recursive{
public static void main(String[] args){
Recursive T = new Recursive();
T.DFS(3);
}
public void DFS(int n) {
if(n==0){
return;
} else{
DFS(n-1); // line 11
System.out.print(n + " ");
}
}
}출력을 담당하는 부분인 System.out.print()를 DFS 함수 아래에 위치
- 이 원리가 스택프레임이다.
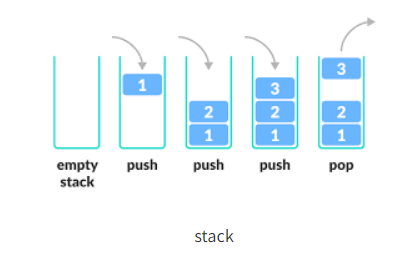
Stack
- LIFO(Last In First Out) 방식으로 가장 나중에 저장된 데이터가 가장 먼저 인출되는 방식으로 동작
DFS 함수 설명(흐름)
-
처음 인자값으로 3이 들어오고 DFS 함수를 실행
-
0이 아니기 때문에 else문을 타게 되고 다시 DFS(n-1) 함수를 타게 된다. 이때, 가장 중요한 것은 처음 DFS(3) 함수는 line 11에 멈춰 있는 상태로 스택에 쌓이게 된다. 즉, System.out.print() 가 실행되지 않은 상태로 스택에 쌓이는 것이다.
-
그 다음은 2가 들어오게 되고, 0이 아니기 때문에 위와 같이 실행된다. 위의 그림과 같이 0이 될 때까지 쌓이게 된다.
-
마지막으로 DFS() 함수에 0이 들어오게 되면 return; 하기 때문에 해당 함수는 종료된다. 이후 스택에 잠시 멈춰있던 함수들이 차례로 실행되기 때문에 1 2 3 순으로 출력된다.
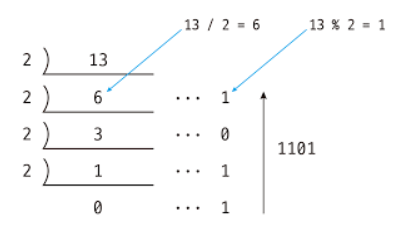
재귀 함수(이진수)
10진수를 2진수로 반환하기 위한 코드 예시
public class Binary{
public static void main(String[] args){
Binary T = new Binary();
T.DFS(13);
}
public void DFS(int n) {
if(n==0){
return;
} else{
DFS(n/2);
System.out.print(n%2 + " ");
}
}
}결과
- 1 1 0 1
설명
원리는 첫 예시와 동일
팩토리얼(Factorial)
팩토리얼 : 수학에서 그 수보다 작거나 같은 모든 양의 정수의 곱
ex)5! = 5 4 3 2 1
재귀함수를 이용한 팩토리얼
public class Factorial{
public static void main(String[] args){
Factorial T = new Factorial();
System.out.println(T.DFS(5));
}
public void DFS(int n) {
if(n==1){
return 1;
} else{
return n*DFS(n-1);
}
}
}결과
- 120
설명
- 재귀를 1에서 멈추는 이유는 팩토리얼은 모든 양의 정수의 곱이기 때문
- 처음 인자 값으로 5가 들어오면 5 DFS(n-1) -> 4 DFS(n-1) ... 반복 후 인자 값이 1이 될 때까지 진행, 스택이 다 쌓였으면 가장 위의 스택부터 꺼내게 됨
1 2 3 4 5 = 120
Queue(큐)
- FIFO(First In First Out) 개념
- 입구와 출구가 모두 뚫려 있는 터널
Public class Main{
public static void (String[] args) {
Queue<Integer> q = new LinkedList<>();
q.offer(1);
q.offer(2);
q.offer(3);
q.poll(); // 1
q.offer(4);
q.poll(); // 2
q.offer(5);
for(int i=0; i<q.size(); i++){
System.out.print(q.peek());
q.add(q.poll());
}
}
}설명
- 순서대로 큐에는 1 2 3 이 들어가게 된다
poll() 함수로 인하여 처음에 들어갔던 1은 사라지게 된다. 즉, 2 3 이 남는다 - offer(4) -> 2 3 4 가 큐에 들어가 있다.
다시 한 번 poll() -> 3 4 - offer(5) -> 3 4 5
- 마지막 반복문
- 처음에 들어있던 3을 출력(peek())
- poll()은 큐에서 가장 앞에 있는 인자를 반환하고 그 값을 큐에서 삭제한다.
- 그 후 add() 로 해당 값을 다시 큐에 넣어줌
- 즉, 큐를 한 바퀴 돌려 출력하게 됨
전역 클래스 Node
DFS와 BFS 모두 사용할 Node 클래스를 미리 선언. 노드는 그래프의 각각의 지점이라 생각하면 된다.
class Node{
int data;
Node lt, rt;
public Node(int val) {
data = val;
lt = null;
rt = null;
}
}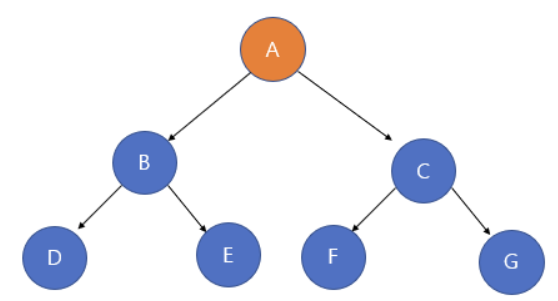
A번 노드는 lt에 해당하는 B번 노드, rt에 해당하는 C번 노드가 있다. 마찬가지로 B번 노드에는 lt에 해당하는 D번 노드, rt에 해당하는 E번 노드가 있다. 이런 식으로 Node 클래스는 val(ex:A)와 lt, rt 값으로 사용될 예정
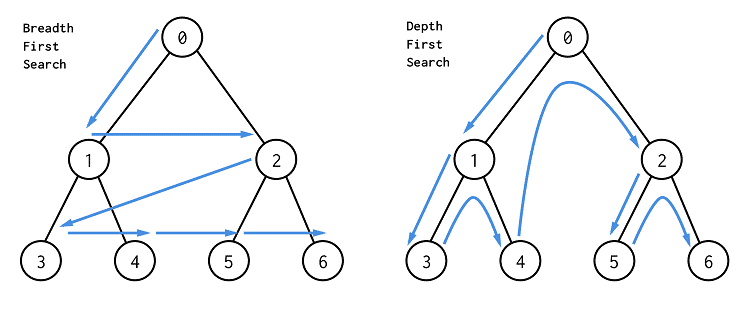
DFS
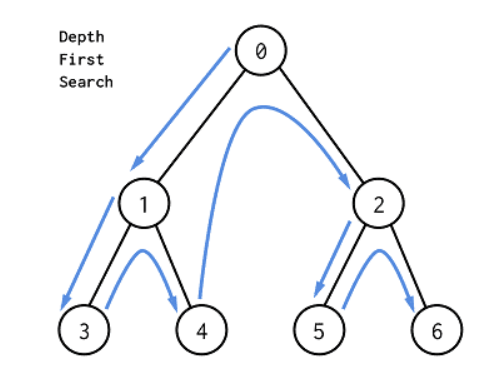
설명
-
DFS는 자기 자신을 호출하는 순환 알고리즘의 형태를 지닌다. 위의 그림처럼 0에서 1로 1에서 3으로 갔을 때 더 이상 갈 곳이 없으면 백 트랙킹(BackTracking)을 해서 다시 1로 가게 된다. 이후에 방문하지 않은 4를 방문하게 되는 형태이다.
-
흔히 미로를 예시로 많이 든다.
-
DFS는 대게 Stack(스택) 을 사용하고 모든 노드를 방문하고자 할 때 사용한다. BFS 보다 더 간단하게 구현되지만 검색 속도 자체는 BFS에 비해 느리다.
public class DFS{
Node root;
public static void main(String[] args){
DFS tree = new DFS();
tree.root = new Node(0);
tree.root.lt = new Node(1);
tree.root.rt = new Node(2);
tree.root.lt.lt = new Node(3);
tree.root.lt.rt = new Node(4);
tree.root.rt.lt = new Node(5);
tree.root.rt.rt = new Node(6);
tree.DFS(tree.root);
}
]- 첫 번쨰로는 위의 사진과 같이 트리 형식으로 노드를 구성.
- 이후 DFS() 함수를 실행
- 인자 값으로 tree.root를 넣었다.
- 첫 노드 값은 0이다.
public void DFS(Node root){
if(root == null) return;
else {
System.out.print(root.data + " ");
DFS(root.lt);
DFS(root.rt);
}
}결과
0 1 3 4 2 5 6
-
위의 그림과 같이 왼쪽부터 순차적으로 깊이 우선 탐색이 실행되는 것을 확인할 수 있다.
-
처음에 DFS(tree.root) 함수를 호출시켰다.
-
즉, DFS 인자값으로 0 이 처음 들어오게 된다.
-
0은 null 이 아니기 때문에 else 문을 타게되고 0을 출력한 후 DFS(root.lt)를 호출한다.
-
즉, 0의 왼쪽 노드인 1을 호출하게 된다.
-
DFS(root.rt)는 스택에 쌓이고 DFS(root.lt)를 실행
-
DFS(root.lt)가 실행되면 인자 값으로 1이 넘어온다.
-
1도 null 이 아니기 때문에 else문을 타게 된다. 1을 출력한 후 DFS(root.lt)를 실행한다.
-
DFS(root.rt)는 스택에 쌓이게 됨.
-
DFS(1의 root.lt ==3) 이 실행되고 현재까지 System.out.print() 로 콘솔에 출력한 것은 0 1 3 이다.
-
그 다음 수행할 것은 lt이다. 하지만 tree에 3의 lt 값은 없다.
-
즉, null 이기 때문에 return; 된다.
-
3에서 백 트랙킹을 해서 1로 다시 넘어오고 스택에 쌓인 DFS(1의 root.rt == 4)가 수행된다.
-
이런 로직을 반복하여 모든 노드를 탐색하게 된다.
이미지 출처 : Code States
BFS
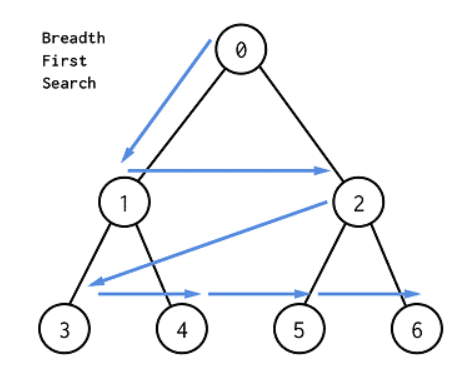
설명
- BFS는 재귀적으로 동작하지 않고 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 큐(Queue)를 사용한다.
- 즉, FIFO 원칙으로 탐색한다.
- 시작 정점으로 부터 가장 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하기 때문에 대게 두 노드 사이의 최단 경로를 찾을 때 주로 사용한다.
BFS Tree(BFS와 동일하게 구성했음)
public class BFS {
Node root;
public static void main(String[] args) {
BFS tree = new BFS();
tree.root=new Node(0);
tree.root.lt=new Node(1);
tree.root.rt=new Node(2);
tree.root.lt.lt=new Node(3);
tree.root.lt.rt=new Node(4);
tree.root.rt.lt=new Node(5);
tree.root.rt.rt=new Node(6);
tree.BFS(tree.root);
}
}BFS 예시
public void BFS(Node root) {
Queue<Node> Q = new LinkedList<>();
Q.offer(root);
int L = 0;
while (!Q.isEmpty()) {
int len = Q.size();
System.out.print(L + " : ");
for(int i = 0; i < len; i++) {
Node current = Q.poll();
System.out.print(current.data + " ");
if(current.lt != null) {
Q.offer(current.lt);
}
if (current.rt != null) {
Q.offer(current.rt);
}
}
L++;
System.out.println();
}
}결과
0 : 0
1 : 1 2
2 : 3 4 5 6
설명
- 결과와 같이 너비 우선 탐색이 실행된 것을 확인할 수 있다.
- 처음은 DFS와 같이 인자 값으로 0 이 들어오고, Queue에 0을 넣게 된다.
- L은 레벨을 뜻하고 초기 값으로는 0으로 셋팅했다.(편의상 넣은 것)
- while 문은 Queue 가 비어있을 때 까지 반복
- 처음에 Queue에는 0 하나만 들어가게 되므로 길이는 1이다.
- 반복문을 돌며 큐에 첫 번째 값(0) 을 꺼내고 그 값을 출력한 후 lt와 rt값이 있다면 큐에 넣는다.
- 큐에는 2개의 값(1, 2) 가 들어있고, 반복문은 길이가 2만큼 돌며 하나씩 꺼내서 값을 출력한다.
- 이번에도 lt와 rt 값이 있다면 큐에 넣는다.
- 쉽게 말해서 0 일때 1, 2를 큐에 넣고, 1일 때 3,4를 넣고, 2일 때 5, 6을 큐에 넣어주는 형식이다.
- 그리고 들어간 순서대로 꺼내져 나오는 것이다.