[자료구조] 그래프(Graph); DFS와 BFS

bien·2025년 12월 4일

자료구조

목록 보기

2/2

그래프(Graph)는 객체(데이터)와 그 객체 간의 연결관계를 표현하는 자료구조를 말한다.
단순히 데이터만 저장하는 것이 아니라, 데이터 사이의 관계가 중요할 때 사용하는 비선형 자료구조이다. 그래프에 대해 알아보자.

1. 그래프 핵심개념

그래프(Graph); 정점과 간선으로 구성된다.
- 정점 (Vertex/Node): 데이터를 담고 있는 객체 (예: 도시)
- 간선 (Edge): 정점들을 연결하는 선 (예: 도로)
  - 공식: G = (V, E) (V: 정점의 집합, E: 간선의 집합)

2. 어원

어원: 그리스어 Graphein(쓰다, 그리다)에서 유래
수학적 유래
- 1736년 수학자 오일러가 '쾨니히스베르크의 다리 건너기 문제'를 풀기 위해, 복잡한 지도에서 땅을 점(Point)으로, 다리를 선(Line)으로 추상화하여 그림을 그렸다.
- 점과 선으로 연결관계를 그려낸(Mapped/Drawn) 모양이라는 뜻에서 그래프 이론(Graph Theory)이라는 이름이 붙었다.
- 즉, 연결 구조를 도식화했다는 의미.

3. 주요 특징

방향성에 따라
- 무방향 그래프(Undirected): 간선에 방향이 없음
- 방향 그래프(Directed): 간선에 방향이 있음
가중치에 따라
- 가중치 크래프(Weighted): 간선에 비용이나 거리가 할당됨

4. 알고리즘

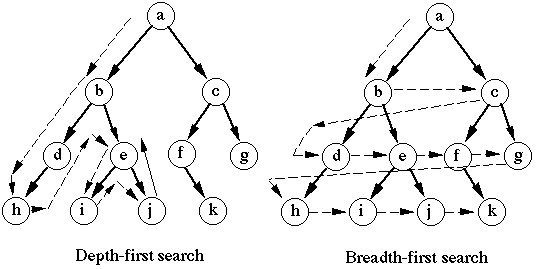
DFS(Depth-First Search, 깊이 우선 탐색)

한 우물만 끝까지 판다!

깊이 우선 탐색으로 vertex(꼭지점)의 자식을 먼저 탐색한다.

설멍: 일단 갈 수 있는 데까지 끝까지 가보고, 막히면 돌아오는 방식
특징:
- 깊게(Deep) 내려간다
- 스택(Stack) 자료구조나 재귀(Recursion) 함수를 사용한다.
- 구현이 비교적 간단하다.
- 사용처: 가능한 모든 경우의 수를 다 찾아야할 때

// visited: 방문 여부 체크 배열
// graph: 연결 상태를 담은 배열
void dfs(int startNode, boolean[] visited) {
	// 1. 체크인: 현재 노드 방문 처리
    visited[node] = true;
    System.out.println(node + " ");
    
    // 2. 목적지 인가? (필요시 종료 조건 추가)
    
    // 3. 연결된 곳 순회
    for (int nextNode : graph[node]) {
    	// 4. 갈 수 있는가? (방문하지 않았다면?)
        if (!visited[nextNode]) {    
        	// 5. 간다! (재귀호출)
	        dfs(nextNode, visited); 
        }
	} 
}

BFS (Breath-First Search, 너비 우선 탐색)

주변부터 꼼꼼히 살핀다!

너비 우선 탐색으로 vertex(꼭지점)의 형제를 먼저 탐색한다.

설명: 나와 가까운 곳 부터 모두 방문하고, 그 다음 멀리있는 곳을 방문한다.
- 호수에 돌을 던졌을 때 물결이 동그랗게 퍼져나가는 모습처럼, 주위부터 방문해 탐색 시작.
특징
- 넓게(Broad) 퍼진다.
- 큐(Queue) 자료구조를 사용한다. (줄 서서 차례대로 방문)
- 출발지에서 목적지까지의 최단 거리를 보장한다.
- 사용처: 최단 경로찾기, 가장 가까운 노드 찾기

void bfs(int startNode, boolean[] visited) {
	Queue<Integer> queue = new LinkedList<>();
    
    // 1. 시작점 큐에 넣고 방문 처리
    queue.offer(startNode);
    visited[startNode] = true;
    
    // 2. 큐가 빌 때까지 반복
    while(!queue.isEmpty()) {
    	// 3. 큐에서 하나 꺼냄 (현재 위치)
        int currentNode = queue.poll();
        System.out.println(currentNode + " ");
        
        // 4. 현재 위치에서 갈 수 있는 모든 곳을 확인
        for (int nextNode : graph[currentNode]) {
        	// 5. 아직 안 가본 곳이라면?
            if (!visited[nextNode]) {
            	// 6. 큐에 넣고 방문 예약(처리)	
                queue.offer(nextNode);
                visited[nextNode] = true;
            }
        }
    }
}

5. 그래프 탐색 핵심원리

가장 많이 헷갈리는 3가지 포인트를 정리해 보자.

1) 왜 visited가 필요할까? — 그래프는 ‘순환한다’

트리(Tree)와 달리 그래프는 노드끼리 서로 순환(Cycle)할 수 있다. (A → B → A → ...)
만약 visited 체크를 하지 않는다면, 알고리즘은 이미 갔던 곳을 또 방문하며 무한 루프(Infinite Loop)에 빠지게 된다.
즉, visited는 "나 여기 왔다 감! 다시 오지 마!"라고 남기는 발자국이자, 재귀 호출을 멈추게 하는 종료 조건의 핵심이다.

2) 탐색함수 1회 실행의 의미 (섬의 개수)

dfs(1) 혹은 bfs(1)을 한 번 호출한다고 해서 무조건 그래프의 모든 노드를 방문하는 것은 아니다. 왜냐하면 그래프는 여러 덩어리(Connected Components)로 분리될 수 있기 때문이다.
즉, 하나의 탐색함수(dfs(), bfs()는 하나의 연결영역만 탐색한다.

1회 실행: 시작 노드와 '연결된' 노드들만 탐색한다. (하나의 덩어리)
전체 탐색: 만약 그래프가 여러 개의 '끊어진 섬(Island)' 형태라면, 방문하지 않은 노드가 없을 때까지 for문을 돌며 탐색 메서드를 여러 번 호출해야 한다.

모든 노드를 확실하게 방문하기 위한 패턴

int islandCount = 0;
for (int i = 1; i <= N; i++) {
    // 아직 방문하지 않은 노드가 있다면? (새로운 섬 발견!)
    if (!visited[i]) {
        dfs(i); // 그 섬을 싹 다 훑어서 true로 만듦
        islandCount++; // 섬 개수 +1
    }
}