Algorithm
1.[프로그래머스] - [1차] 캐시(Java)

[1차] 캐시 Solution LRU(Least Recently Used) Algorithm : 가장 오랫동안 참조되지 않은 페이지를 교체하는 기법
2.[프로그래머스] - 기지국 설치(Java)

기지국 설치N이 최대 2억개이므로 배열에 상태를 저장하면서 계산하는 것은 불가능하다고 생각하였고, 범위 안의 아파트의 개수에 대한 기지국의 개수를 한번에 구할 수 있는 방법이 있다고 판단하였다.stations 배열은 오름차순으로 정렬되어 있으므로, 별도의 index를
3.[프로그래머스] - 미로 탈출 명령어

미로 탈출 명령어k가 최대 2500까지 가능하므로 dfs, bfs 모두 가능하였고, 나는 bfs로 풀었다.dfs로 풀었으면 정렬이 필요없이 d -> l -> r -> u 순서대로 dfs를 돌리면 된다.사전순으로 가장 빠른 경로를 답으로 채택하므로, 우선순위 큐를 사용하
4.버블 정렬

서로 인접한 원소를 비교하여 교환하는 정렬 알고리즘배열의 두 수(a, b)를 선택한 뒤, 그 두 수를 비교하여 오름차순, 내림차순에 맞게 정렬한다. 오름차순이라면 a < b, 내림차순이라면 a > b 이어야 하며, 이를 배열의 처음부터 끝까지 반복한다.
5.삽입 정렬
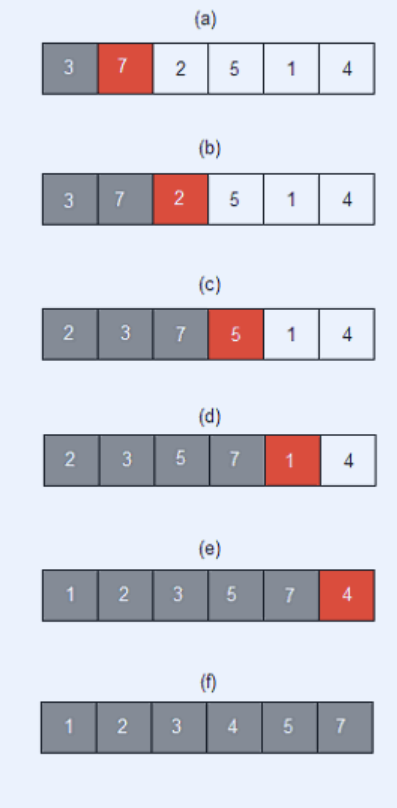
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 위치를 찾아 삽입하는 정렬 알고리즘최악 시간복잡도 : 비교 - O(n^2) 교환 - O(n^2)최선 시간복잡도 : 비교 - O(n) 교환 - O(1)평균 시간복잡도 : 비교 - O(n^
6.[백준] - 퀵 정렬3(24092)

퀵 정렬3퀵 정렬을 사용하여 정렬을 진행 중에 B배열과 일치하는지 여부를 판별하는 문제이다.pivot은 오른쪽 맨 끝 원소를 기준으로 퀵 정렬을 하도록 문제에서 제시되어 있다.
7.[프로그래머스] - 셔틀버스(Java)

타임 테이블 배열의 String 원소를 int형의 분단위로 변경하여 시간순 정렬한 타임리스트를 생성한다. 버스 도착시간에 맞춰 버스에 탈 수 있는 시간대의 사람을 타임리스트에서 찾는다. 콘은 마지막 버스를 타는 것이 가장 늦은 시각이다.마지막 버스를 탈 수 있다
8.[프로그래머스] - 경주로 건설

경주로 건설0,0 지점에서 N-1, N-1 지점까지 도착할 때 최소비용을 구하는 문제이다.현재 방향을 그대로 유지하면서 진행할 경우 비용은 +100, 방향을 바꾸는 경우는 +600의 비용이 추가되며, dfs와 bfs 두 가지 모두 풀이가 가능하다.DFS기존 visite
9.이분 탐색(Binary Search - Lower Bound, Upper Bound)

이분 탐색은 데이터가 정렬되어 있는 배열에서 특정한 원소를 찾는 알고리즘이다. 이분 탐색을 사용하기 위해서는 원소가 오름차순 또한 내림차순으로 정렬되어 있어야 한다.이분 탐색 과정은 다음과 같다(오름차순 정렬이 되어있는 상태).찾는 원소를 targetm, 찾고자 하는
10.[백준] - 개똥벌레

개똥벌레높이 h에서 석순과 종유석을 최소의 개수로 뚫고, 그 최소에 해당하는 높이가 몇가지 있는지 찾는 문제이다.list 에 석순과 종유석의 높이를 넣고, 정렬하여 찾고자 하는 높이 h보다 크거나 같은 종유석과 석순의 높이를 찾았다.이때 이분 탐색을 통하여 h보다 크거
11.[프로그래머스] - 입국 심사

입국 심사(https://school.programmers.co.kr/learn/courses/30/lessons/43238입국 심사를 받는 데 걸리는 최솟값을 구하는 문제이다.n명이 가장 빠른 심사관에게만 검사를 받는다면 걸리는 시간은 n times0이며,
12.[프로그래머스] - 다단계 칫솔 판매

다단계 칫솔 판매추천인을 계속해서 찾아나가야되므로, 빠르게 찾을 수 있는 map을 사용하였다.key값으로 자신의 이름, value로 클래스를 하나 만들어서 추천인 이름과, 자신의 이익을 기록하였다.
13.[백준] - 회전하는 큐

회전하는 큐큐의 크기 N이 주어질 때, N개 안에서 최소한의 시프트로 수를 뽑아내는 문제이다.뽑아내려는 수의 위치를 알고 있을 때, 전체 큐의 사이즈에서1) 중간위치보다 왼쪽에 있다면 왼쪽 시프트2) 중간위치보다 오른쪽에 있다면 오른쪽 시프트하여 뽑고자 하는 원소를 큐
14.[백준] - 행운의 바퀴

행운의 바퀴회전수와 회전했을 때 나오는 문자를 입력으로 받아, 최종적으로는 마지막 문자로부터 시계방향으로 출력하는 문제이다.단 알 수 없는 문자는 "?"로 출력, 나올 수 없는 경우는 "!"를 출력한다.나올 수 없는 경우는 다음과 같다.이 경우는 "!"를 출력한다.양
15.[프로그래머스] - 1,2,3 떨어트리기

1,2,3 떨어트리기
16.DP(Dynamic Programming)

DP(Dynamic Programming)는 먼저 작은 부분 문제들의 해들을 구하고 이들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 문제를 해결하는 알고리즘 설계 기법이다.DP를 적용하려는 문제는 다음과 같은 조건을 가지고 있어야 한다.
17.[프로그래머스] - 정수 삼각형

정수 삼각형꼭대기에서 바닥으로 내려갈 때 양쪽 아래 대각선으로만 이동 가능하고, 이동 시 값을 더하여 최종적으로 바닥의 최대 값을 찾는 문제이다.dp를 사용하여 현재 위치에서 이전의 값에서 가져올 수 있는 가장 큰 값을 가져오는 것을 반복하면서 바닥으로 내려가면 결과적
18.[프로그래머스] - 등굣길

등굣길이동방향이 아래와 오른쪽밖에 없으므로 현재 위치에서 올 수 있는 방향은 위와 왼쪽 방향에서 오는 것이다. 따라서 현재 위치에 도달하는 방법의 수는 (왼쪽 칸까지 오는 방법의 수) + (위쪽 칸까지 오는 방법의 수) 가 된다.단, 가장 위쪽 칸의 경우는 왼쪽에서 오
19.[코드트리] - 아름다운 수열

아름다운 수열
20.[코트트리] - Carry 피하기

Carry 피하기
21.[코드트리] - 연속되는 수

연속되는 수
22.[백준] 27067 데이터 순서 복원

1번째 위치는 1, 2번째 위치는 2... 와 같이 각 위치에 가중치를 부여하여 해당 숫자의 총 가중치 합을 구한다. 이 때, 항상 변형된 데이터는 원래의 위치보다 앞으로 가도록 변형되어 있으므로 가장 가중치가 낮은 값은 위치가 변경되었을 가능성이 크다.
23.[코드트리] - 무~

무~N번째 문자를 찾을 수 있는 depth를 구한 후 재귀를 통해 정답을 찾았다.이전 depth의 부분에 N번째 위치가 포함된다면, 재귀를 통하여 depth를 낮추면서 t가 0이 될 때 정답을 구할 수 있다. 그 외에는 현재 depth인 t에 따라 정답을 구할 수 있다
24.[코드트리] - 격자 밟기

격자 밟기
25.[코드트리] - 나무박멸

나무박멸문제에서 주어진 순서대로 진행하면 되는 시뮬레이션 문제이다.