플로이드-와샬 알고리즘

https://blog.naver.com/ndb796/221234427842
위의 블로그 글과 위키백과를 참고하였습니다.

이번주의 알고리즘은 플로이드-와샬 알고리즘이다.
최단 경로 알고리즘 중 하나로 기본적으로는 다익스트라 알고리즘과 비슷하다.
코딩 테스트에 은근히 자주 나오는 알고리즘이기도 하니 정리해 두기로 했다.
다음 게시물에서 다익스트라 알고리즘에 대해서도 설명할 것이다.

알고리즘 설명

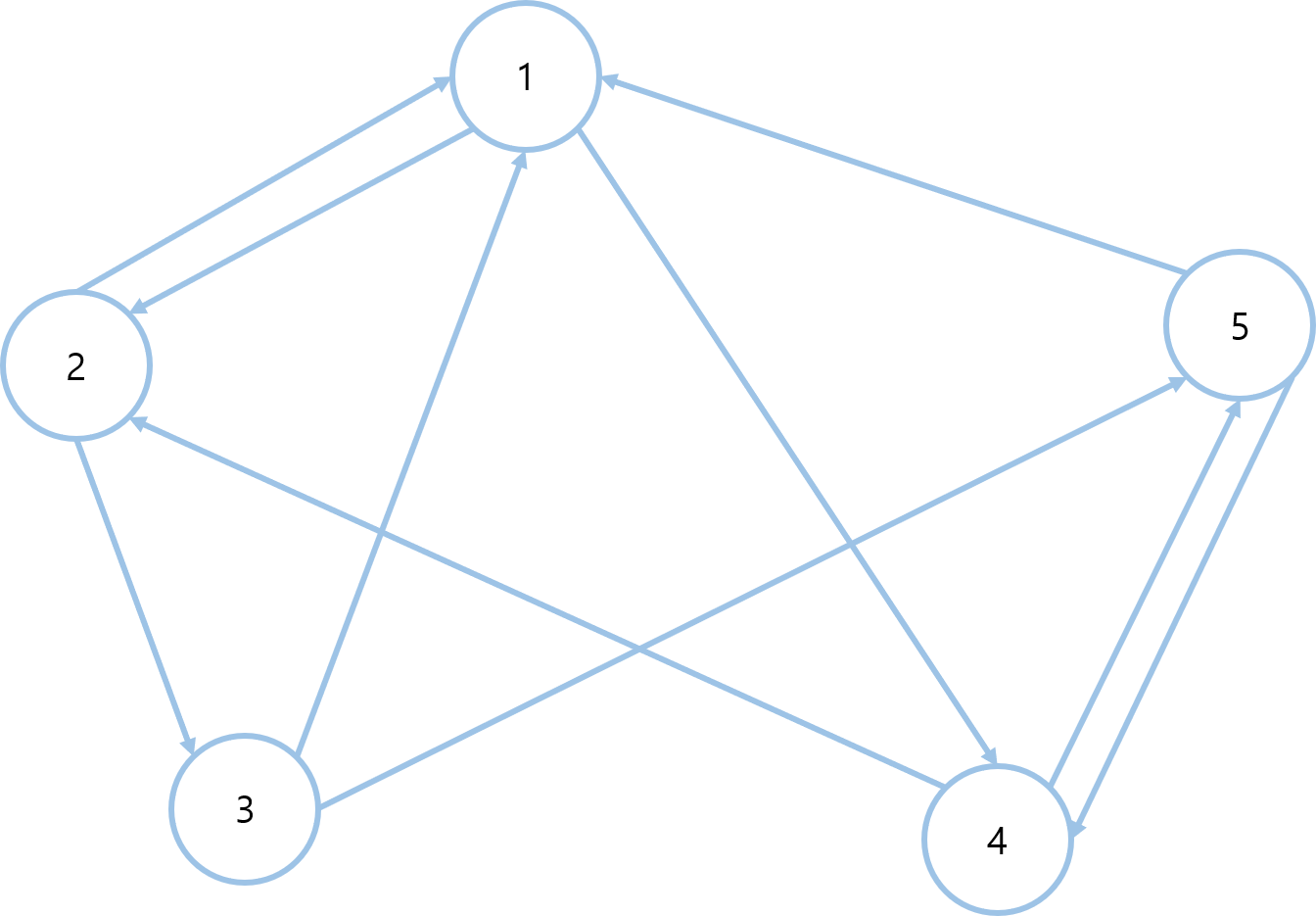
플로이드-와샬 알고리즘은 모든 정점에서 모든 정점으로의 최단 경로를 구한다.

시작하기에 앞서 최소 비용 테이블을 초기화 한다.

아직 경로가 없는 경우에는 infinite(아주 큰 수)로 초기화한다.
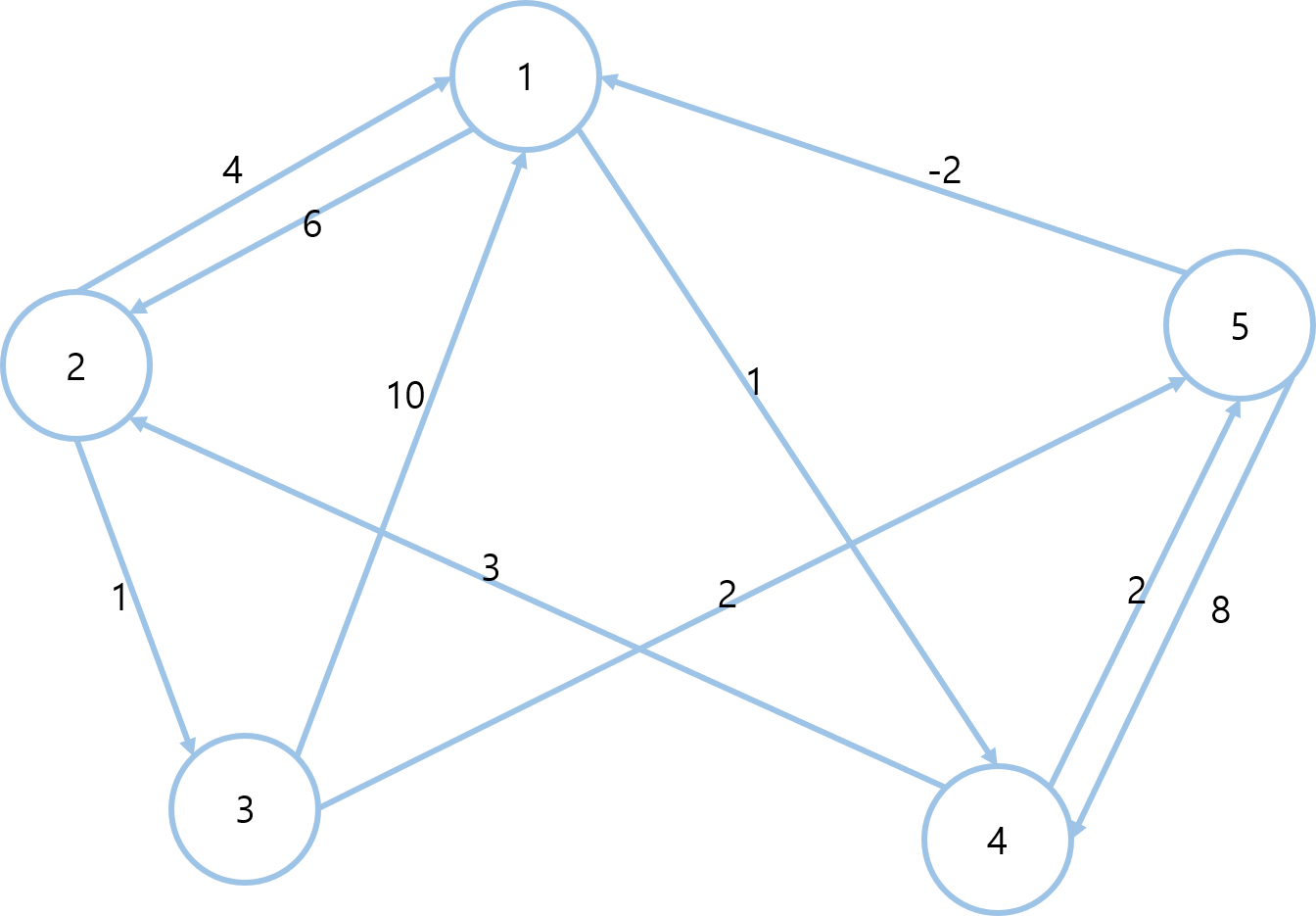
플로이드-와샬 알고리즘에서는 '거쳐가는 정점'을 기준으로 비용 테이블을 업데이트 해야 한다.
이를 위해 반복문을 돌며 현재 최소비용 vs 정점 a를 거쳐가는 최소 비용을 비교한 후 더 적은 쪽으로 업데이트한다.

위의 테이블은 1을 거쳐가는 경우에 대해 비용을 갱신한 테이블이다.
예를 들어, 5에서 2로 바로 가는 경로는 처음에 없었기 때문에 초기 테이블에는 inf로 초기화되어 있었지만, 위의 테이블에서는 5에서 1을 거친 후 2로 가는 경로의 비용 4로 업데이트 되었다. (5->1 비용 -2, 1->2 비용 6 이므로 합치면 4)
같은 방법으로 모든 정점을 확인하고 비용 테이블을 업데이트 하면 원하는 결과 테이블을 얻을 수 있다.
플로이드-와샬 알고리즘을 사용하면 가중치가 음수인 경우에 대해서도 최단 경로를 파악할 수 있다.
그러나 시간 복잡도가 O(N^3)이기 때문에 실행 시간이 길어진다는 단점이 있다.

C++ 코드

#include <iostream>

using namespace std;

int number = 5;
int inf = 99999;

// 초기 테이블
int arr[5][5] = {
    {0,6,inf,1,inf},
    {4,0,1,inf,inf},
    {10,inf,0,inf,2},
    {inf,3,inf,0,2},
    {-2,inf,inf,8,0}
};

void floydWarshall(){
    // 결과 테이블
    int d[5][5];

    // 결과 테이블에 값 복사
    for(int i=0; i<number; i++){
        for(int j=0; j<number; j++){
            d[i][j] = arr[i][j];
        }
    }

    // k번 노드를 거쳐가는 경우에 대해 결과테이블 갱신
    for(int k=0; k<number; k++){
        for(int i=0; i<number; i++){
            for(int j=0; j<number; j++){
                if(d[i][k] + d[k][j] < d[i][j]){
                    d[i][j] = d[i][k] + d[k][j];
                }
            }
        }
    }

    for(int i=0; i<number; i++){
        for(int j=0; j<number; j++){
            cout.width(3);
            cout<<d[i][j];
        }
        cout<<endl;
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    floydWarshall();

    return 0;
}

백준 플로이드-와샬 알고리즘 문제집

https://www.acmicpc.net/problemset?sort=ac_desc&algo=31