트리는 편리한 구조를 전시하는 것 외에 효율적인 탐색을 위해 사용하기도 한다.
그 중 이진 트리(binary tree)와 이진 탐색 트리(binary search tree)를 알아보자.
1. 이진 트리(Binary tree)
자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉜다.
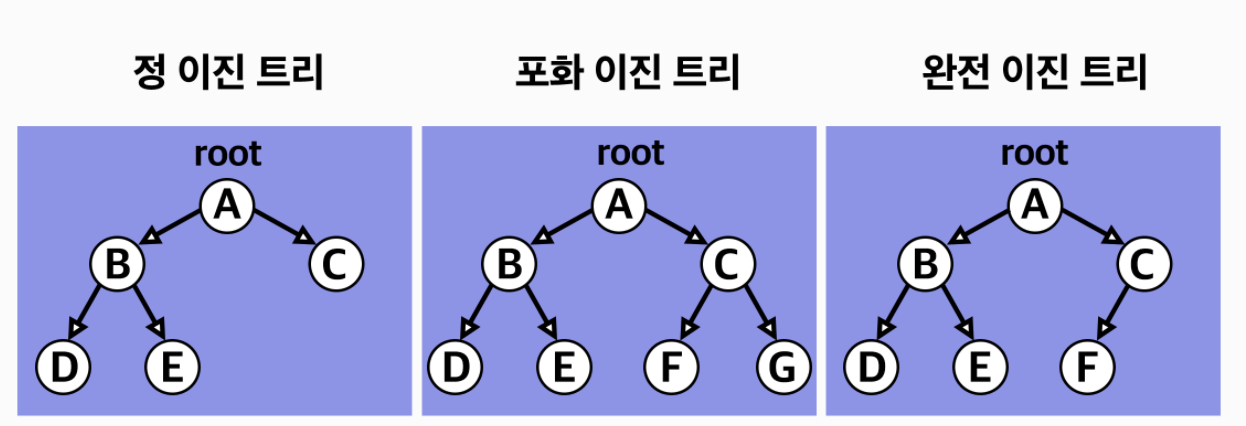
- 완전 이진트리(Complete binary tree)
마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하며, 마지막 레벨의 노드 왼쪽에는 가득채워져 있어야 한다. - 정 이진 트리(Full binary tree)
각 노드가 0개 또는 2개의 자식 노드를 갖는다. - 포화 이진 트리(Perfect binary tree)
정 이진 트리면서 완전 이진 트리인 경우.
2. 이진 탐색 트리(Binary Search Tree)
이진 트리이면서, 특정 조건에 맞는 순서를 갖는 트리이다.
이진 탐색 트리의 모든 왼쪽 자식들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자식들은 루트나 부모보다 큰 값을 가진다.
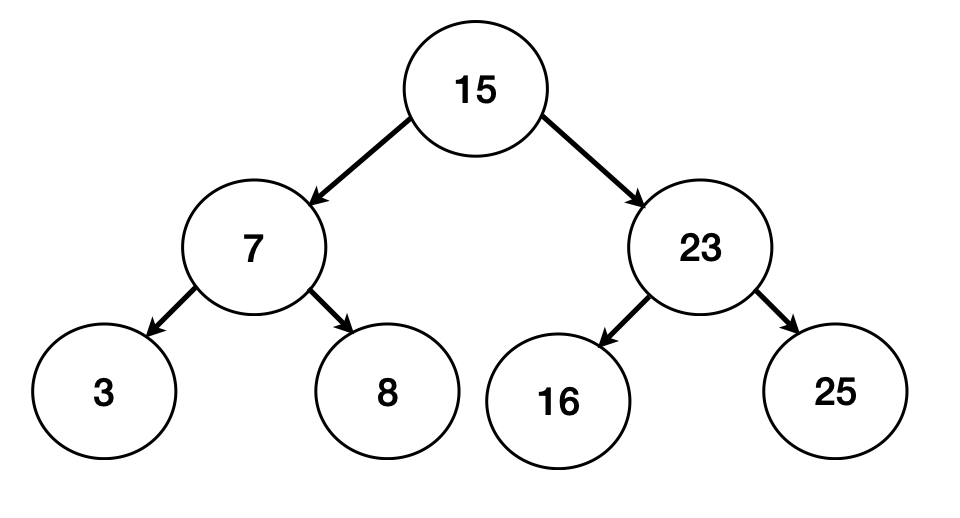
이진 탐색 트리는 균형 잡힌 트리가 아닐 때 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 가능성이 있기 때문에 삽입과 삭제마다 트리의 구조를 재조정하는 균형 이진 탐색 트리라는 개념이 등장했고, 균형을 잡기 위한 알고리즘을 도입할 수 있다.
@균형 이진 탐색 트리 참조 블로그
https://jackpot53.tistory.com/17.
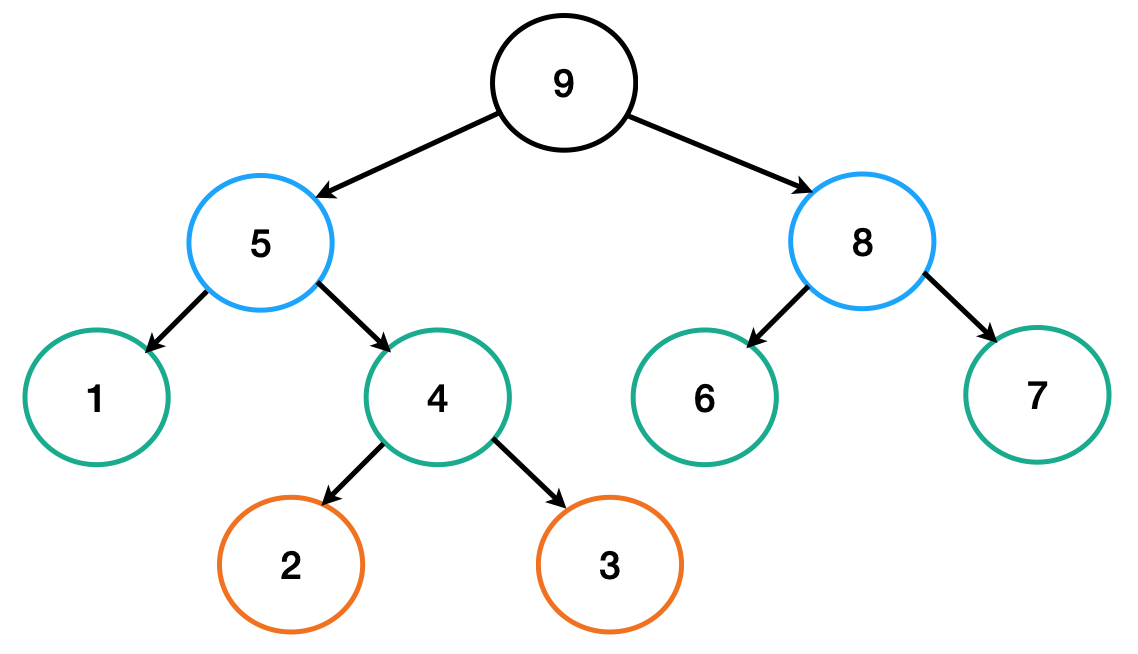
트리순회(Tree traversal)
특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회라고 한다.
모든 트리를 순회 할 수 있는 방법
-
전위 순회
제일 처음 루트를 방문하고, 루트 기준 왼쪽 노드들을 둘러본 뒤, 왼쪽 노드 탐색이 끝나면 오른쪽 노드 탐색을 한다.
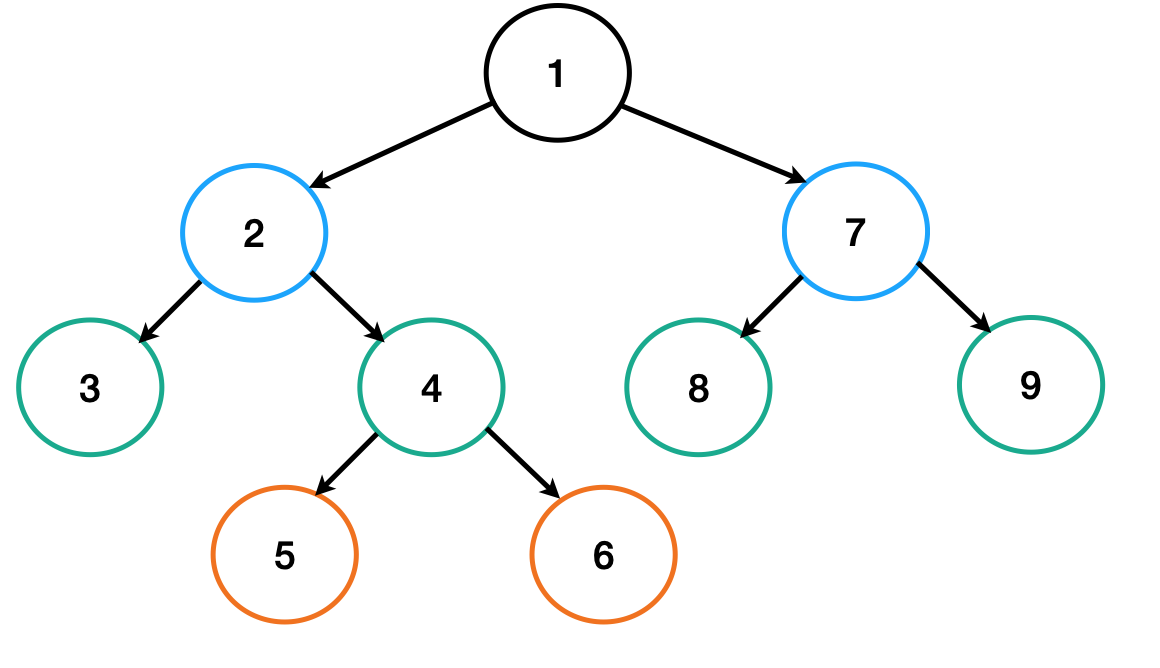
-
중위 순회
루트를 가운데 두고, 제일 왼쪽 끝에 있는 노드부트 순회하면다. 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동해 탐색한다.
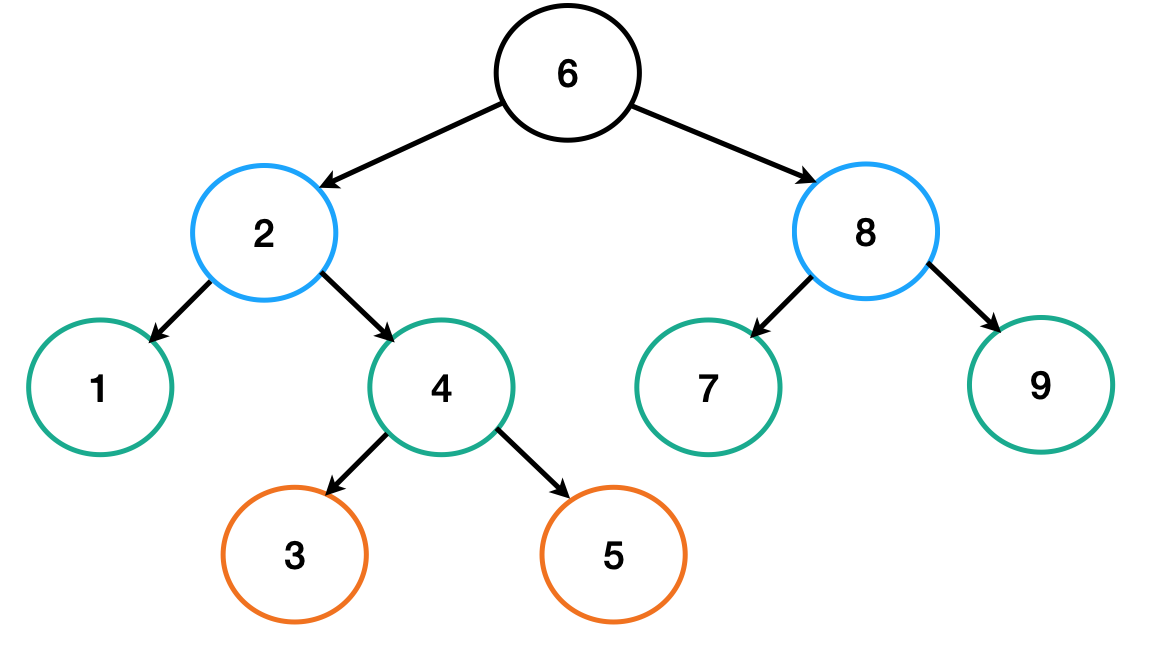
- 후위 순회
루트를 제일 마지막으로 순회한다. 제일 왼쪽 끝에 있는 노드부터 순회하여, 루트를 거치지 않고 오른쪽으로 이동해 순회한뒤 제일 마지막으로 루트를 방문한다.