[Programmers] N으로 표현

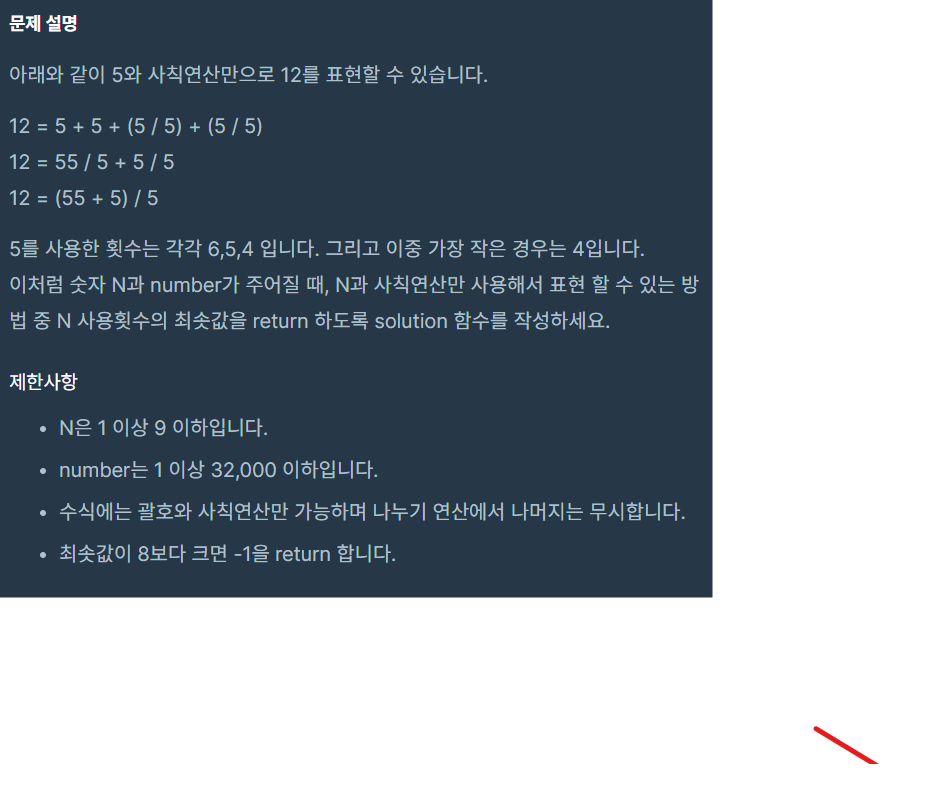
문제

고민해보다가 다른 사람 풀이를 참고했다. 아마 혼자 고민했으면 3달정도 걸렸을 듯 하다.

DP문제면 뭔가 값을 기록하고 이용해야한다는 건 알겠는데, 그게 어렵다.
처음 생각한 건 재귀를 이용해서 사칙연산을 한 값을 다시 넘겨주면서 연산횟수가 8번이 될 때까지 경우의 수를 탐색하는 거였는데, segmentation fault 오류가 났고 원인을 찾지 못했다.

이 문제의 핵심 아이디어는 i+j = k일 때, N을 k번 쓴 경우는 N을 i번 쓴 경우와 j번 쓴 경우에 대해 사칙연산을 수행한 것이다.

unordered_set을 이용해 중복되는 경우에 대해 최적화 하였다.

dp문제를 풀 때 아직 겪어본 경우를 벗어나서는 생각을 잘 못 하는 것 같다.

참고 블로그 링크

코드

#include <string>
#include <vector>
#include <unordered_set> 
#include <iostream>
using namespace std;

int solution(int N, int number) {
    int answer = 0;
    vector<unordered_set<int>> dp(9);
    if (N == number) return 1;
    
    dp[1].insert(N);
    for(int i=2; i<dp.size(); i++){  
        int c=N;
            for(int j=1; j<i; j++){
                c = c*10+N;
            }
        dp[i].insert(c);  
        
        for(int j=1; j<i; j++){
            unordered_set<int> first = dp[j];
            unordered_set<int> second = dp[i-j];
            for(int a: first){
                for(int b: second){
                    dp[i].insert(a+b);

                    if (a - b > 0) dp[i].insert(a - b); 
                  
                    dp[i].insert(a*b);

                    if (a / b > 0) dp[i].insert(a / b);
                   }
            }
              
        }

         if (dp[i].find(number)!=dp[i].end())
            return i; 
    }
    
    return -1;
}