<Algorithm> 트리 순회

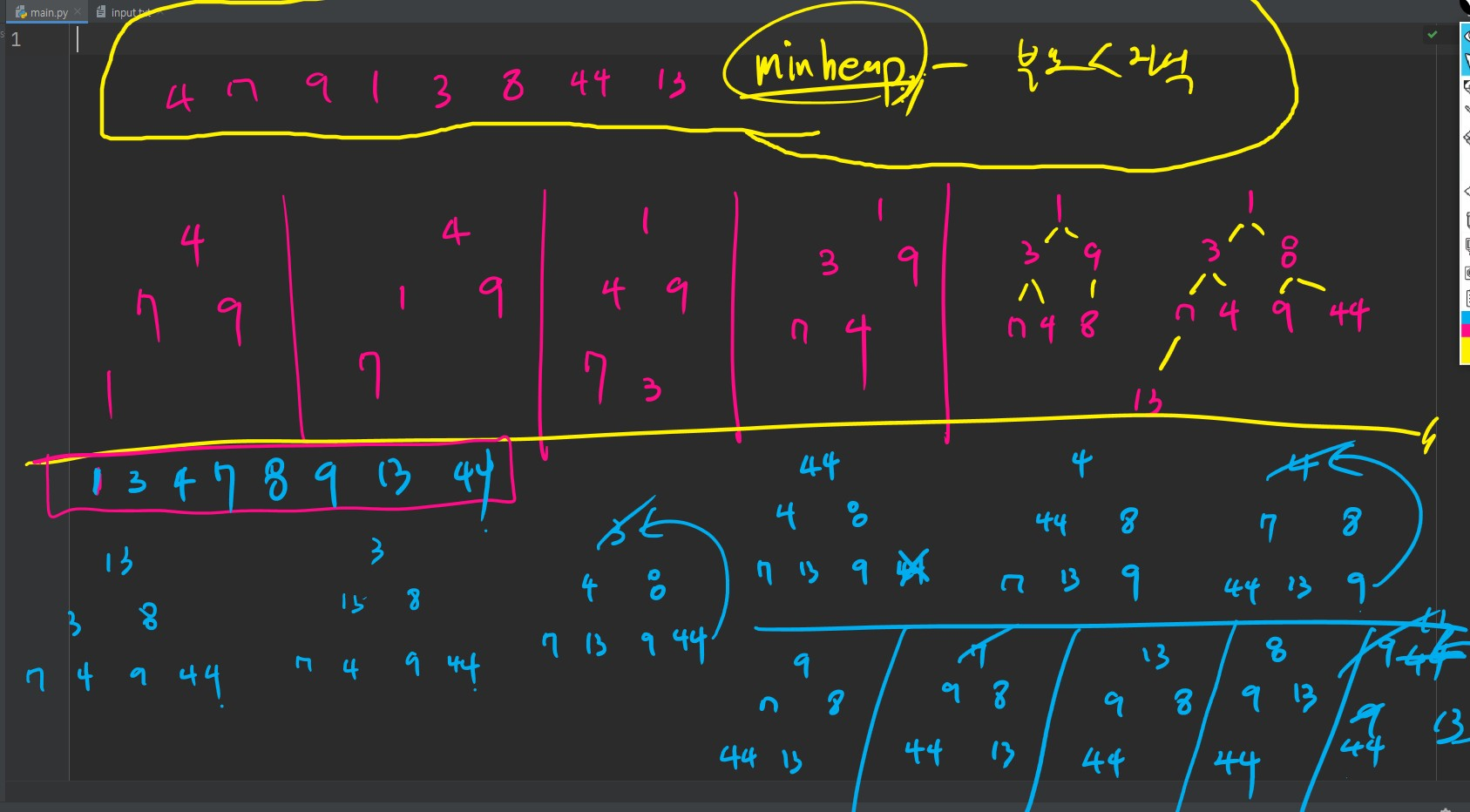
tree

트리의 순회 (탐색하면서 출력순서)

preorder(전위순회)

postorder(후위순회)

inorder(중위순회)

arr=" ABCDEFG"

def preorder(now):

    if now>len(arr)-1: return
    print(arr[now],end=' ')
    preorder(now*2)
    preorder(now*2+1)

def postorder(now):

    if now>len(arr)-1: return

    postorder(now*2)
    postorder(now*2+1)
    print(arr[now], end=' ')

def inorder(now):

    if now>len(arr)-1: return

    inorder(now*2)
    print(arr[now], end=' ')
    inorder(now*2+1)


preorder(1) # 전위순회
print()
postorder(1) # 후위순회
print()
inorder(1) # 중위순회

Heap 자료구조

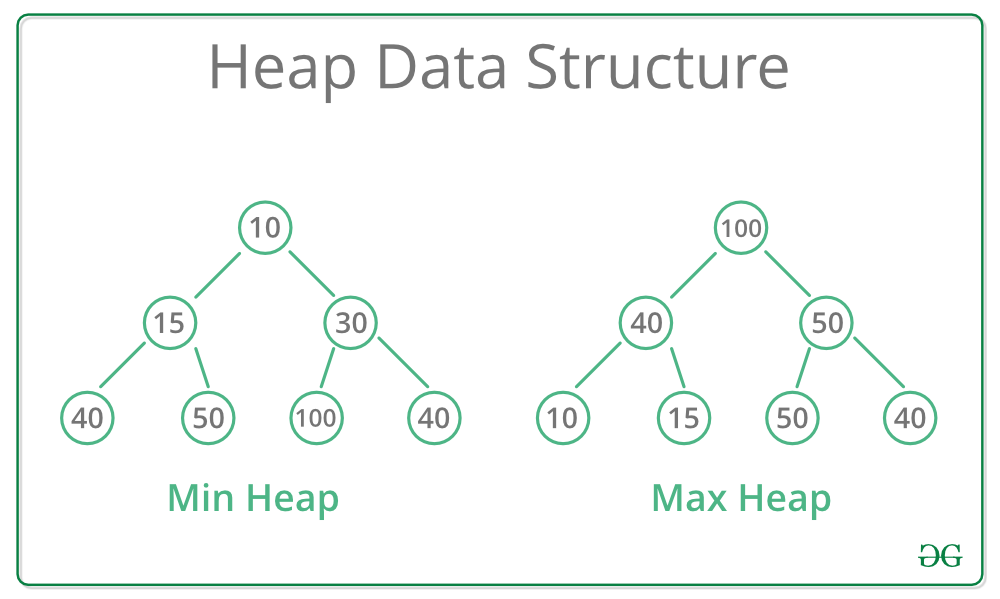
# max heap
arr=[4,7,9,1,3,8,44,13]
heap=[0]*20     # MAX HEAP    1차원 리스트
hindex=1

def insert(value):
    global heap,hindex

    heap[hindex]=value
    now=hindex    # now - 처음에는 방금 추가가 된 아이
    hindex+=1

    while 1:
        parents=now//2 # 부모인덱스
        if parents==0: break #부모인덱스가 0 (처음 루트노드에 값이 들어가면 비교할 것이 없으니까 )
        if heap[parents]>heap[now]:break # 부모>자식
        heap[parents],heap[now]=heap[now],heap[parents] #자식이 더 크면 swap
        now=parents # 스왑 후 그 위의 부모랑 또 비교


def top():
    global heap,hindex
    return heap[1]    # 루트노드 값 반환 (우선순위가 가장 높은 값 반환)

def pop():
    global heap, hindex
    heap[1]=heap[hindex-1]
    heap[hindex-1]=0
    hindex-=1

    now=1
    while 1:
        son=now*2 # 왼쪽자식
        rson=son+1 # 오른쪽 자식
        if heap[rson]!=0 and heap[son]<heap[rson]: son=rson #오른쪽 자식이 있으면 #오른쪽 자식과 왼쪽자식 비교 (부모랑 비교할 대상 정하기)
        if heap[now]>=heap[son]:break # 부모(now) 랑 아들이랑 비교
        heap[now],heap[son]=heap[son],heap[now] #부모가 더 작으면 swap
        now=son # swap 후 또 그 아래의 아들과 비교

for i in range(len(arr)):
    insert(arr[i])          # 이진트리의 형태로 저장을 하는

for i in range(len(arr)):
    print(top(),end=' ')    # 1번인덱스 출력
    pop()                   # 트리에서 값 제거 후 자식들과 비교