🎯 To-do List
☑️ 금요일 저녁 : CSAPP 3.7절 발표 (개념 깊이)
☑️ 토요일 점심 먹고 : 동적 프로그래밍 발표
☑️ 월요일 점심 먹고 : Knapsack Problem
📚 Journal
운영진 티타임 가졌는데 코치 분들은 3분 중 2분이 블로그 안 쓴다고 함.
근데 왜 우리한텐 TIL 쓰라고 시키는거지?
일단 기록이 남아서 성취감 느껴지니까 써보자.
신입은 아무것도 없으니 블로그라도 끄적여야 되는거고,
시니어는 글쪼가리보단 자기가 한 일로 증명해야 하니까 그런 거 아닐까?
코치진이 계속 강조하는게 2가지인듯
1. 우리한테 물어보지 말고 궁금증이나 어려움을 스스로 찾고 생각하는 힘을 길러라
2. 동료 학습 하면서 배워라
📝 배운 것들
🏷️ 배열의 메모리 사용량
파이썬에서 배열 1개는 얼마만큼의 메모리를 차지하는가
파이썬에서 배열, 특히 리스트의 메모리 사용량은 다음 요소들에 의해 결정됩니다:
- 리스트 자체의 오버헤드: 파이썬 리스트는 배열의 포인터와 몇 가지 메타 정보를 포함하고 있습니다. 파이썬 64비트 시스템에서 빈 리스트는 약 64바이트의 메모리를 사용합니다.
- 요소의 메모리 사용량: 리스트에 포함된 각 요소는 자체 메모리를 차지합니다. 예를 들어, 정수는 약 28바이트를 차지하며, 객체나 문자열은 그 크기에 따라 다릅니다.
- 추가 오버헤드: 리스트는 동적 배열이므로 메모리 재할당을 피하기 위해 여유 공간을 갖습니다.
예시
- 빈 리스트: 약 64바이트
- 정수를 포함하는 리스트: 각 정수마다 약 28바이트 추가
이 값을 사용하여 리스트의 메모리 사용량을 대략적으로 계산할 수 있습니다.
계산 예시
import sys
empty_list = []
print(sys.getsizeof(empty_list)) # 빈 리스트의 메모리 사용량 : 56
int_list = [1, 2, 3, 4, 5]
print(sys.getsizeof(int_list)) # 정수 리스트의 메모리 사용량 : 104
string_list = ["a", "b", "c"]
print(sys.getsizeof(string_list)) # 문자열 리스트의 메모리 사용량 : 88이 예시를 통해 각 리스트의 메모리 사용량을 확인할 수 있습니다.
🏷️ 동적 프로그래밍
(= dynamic programming, DP)
어떤 결과를 저장하면서 문제를 푸는데,
그 결과를 앞으로의 풀이에 계속 활용하는 느낌인 것 같다.
동적 프로그래밍 자체는 이전에도 사용해본 적 있었을듯.
하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것
이렇게 이해하면 될듯
"컴퓨터 과학이 여는 세계"에서는 다이나믹 프로그래밍을 본질적인 의미를 더 살려서 기억하며 풀기로 더욱 적절하게 번역하였다.
이게 제일 간단한 정의인듯
🔷 사용 조건
DP가 적용되기 위해서는 2가지 조건을 만족해야 한다.
1) Overlapping Subproblems(중복 부분 문제)
문제를 작게 쪼개고 그 중 하나만 풀면 똑같은 문제는 연산 생략 가능할 때.
2) Optimal Substructure(최적 부분 구조)
문제를 작게 쪼개고 작은 문제 푼 결과 활용하면 큰 문제도 풀릴 때.
🔷 종류
1) 탑-다운 방식
큰 문제에서 시작해서 작은 문제로 쪼갠다
재귀적으로 호출하여 문제를 해결하는 방식
2) 바텀-업 방식
작은 문제를 합해서 큰 문제를 푼다
반복문으로 작은 문제를 풀어서 문제를 해결한다
⚔️ 백준
📌 1388 바닥 장식
import sys
input = sys.stdin.readline
# N은 세로 길이, M은 가로 길이
N, M = map(int, input().split())
floor = []
visitied = []
for _ in range(N):
floor.append(input().strip())
# 세로와 가로 길이 바꿈
floor_mirror = ['' for _ in range(M)]
# 행렬 90도 회전
for i in range(M-1,-1,-1):
for j in range(N):
floor_mirror[M-1-i] += floor[j][i]
cnt = 0
for i in range(N):
onlyHorizon = floor[i].split('|')
for horizon in onlyHorizon:
if horizon:
cnt += 1
for i in range(M):
onlyVertical = floor_mirror[i].split('-')
for vertical in onlyVertical:
if vertical:
cnt += 1
print(cnt)↑ 정답 코드
하나는 행마다 split('-')
다른 하나는 행렬을 90도 회전시킨 후에 split('|')
직관적으로 잘 풀었다고 생각했는데
N, M = map(int, input().split())
Floor = [None] * N
count_garo = 0
count_sero = 0
for i in range(N):
Floor[i] = input()
for i in range(N):
for j in range(M):
if Floor[i][j] == '-':
count_garo += 1
if j != 0 and Floor[i][j - 1] == '-':
count_garo -= 1
if Floor[i][j] == '|':
count_sero += 1
if i != 0 and Floor[i - 1][j] == '|':
count_sero -= 1
print(count_garo + count_sero)↑ 남의 정답 코드
이게 훨씬 깔끔하고 좋은듯?
굳이 상하좌우 판단하는게 아니라 일단 더해주고
가로면 왼쪽 칸, 세로면 위쪽 칸이 중복인지 판단해서 빼줄까 말까 결정하는 알고리즘인듯
📌 2667 단지번호붙이기
import sys
input = sys.stdin.readline
# 지도 한 변 크기 N
N = int(input())
apt = [[] for _ in range(N)]
for i in range(N):
buildings = input().strip()
for building in buildings:
apt[i].append(building)
# 지도 순회 돌리면서
# visitied에 체크 안돼있으면 dfs 시작
# dfs 돌면서 visitied에 체크 싹 다 때린 후에
# dfs 끝나면 cnt += 1
visitied = [[] for _ in range(N)]
for i in range(N):
for j in range(N):
visitied[i].append('0')
def dfs(i,j):
global cnt
cnt += 1
visitied[i][j] = '1'
di = [1,-1,0,0]
dj = [0,0,1,-1]
for k in range(4):
i_udlr, j_udlr = i+di[k], j+dj[k]
if 0 <= i_udlr < N and 0 <= j_udlr < N:
if apt[i_udlr][j_udlr] == '1':
if visitied[i_udlr][j_udlr] == '0':
visitied[i_udlr][j_udlr] = '1'
dfs(i_udlr,j_udlr)
return cnt
cnt_list = []
total_group = 0
for i in range(N):
for j in range(N):
if apt[i][j] == '1' and visitied[i][j] == '0':
cnt = 0
total_group += 1
cnt_list.append(dfs(i,j))
print(total_group)
cnt_list.sort()
for cnt in cnt_list:
print(cnt)↑ 정답 코드
푸는데 급급해서 최적화고 뭐고 막 풀었는데
import sys
input=sys.stdin.read
def dfs(x,y):
if x<0 or y<0 or x>=n or y>=n:
return 0
if grid[x][y]==0:
return 0
grid[x][y]=0
count=1
count+= dfs(x-1,y)
count+= dfs(x+1,y)
count+= dfs(x,y-1)
count+= dfs(x,y+1)
return count
data=input().strip().split()
n=int(data[0])
grid=[]
index=1
for i in range(n):
grid.append([int(x) for x in data[index]])
index+=1
result=[]
for i in range(n):
for j in range(n):
if grid[i][j]==1:
result.append(dfs(i,j))
result.sort()
print(len(result))
for count in result:
print(count)↑ 남의 정답 코드
이게 더 깔끔한듯
📌 2748 피보나치 수 2
n = int(input())
# 동적 프로그래밍
# 하향식 접근법 사용해보기
# n이 될때까지 이전 결과 합하기
def pibo(fn_1, fn, cnt):
global n
if cnt <= n:
result = pibo(fn,fn_1+fn,cnt+1)
return result
else:
return fn
if n==1:
print(1)
elif n==2:
print(1)
else:
print(pibo(1,1,3))동적 프로그래밍의 쌩기초를 알려주는 문제.
원래 이런 문제는 굳이 안 적는데 맨 처음이라 적어봤다.
📌 1904 01타일
00 또는 1로 만들 수 있는 n자리 이진수
동적 프로그래밍으로 접근 (결과를 기록)
정공법 : 00과 1로 경우의 수 만들기
우회법 : 2진수 경우의 수에서 00이 아닌거 빼기?
1 경우의 수 : 1
2 경우의 수 : 00, 11
3 경우의 수 : 100,001, 111
4 경우의 수 : 0000, 1100, 1001, 0011, 1111
5 경우의 수 : 11111, 00111, 10011, 11001, 11100, 00001,00100, 10000
3 경우의 수는 2 경우의 수에서 바로 파생되기 어려운 것 같음.
일종의 규칙이 있는건가?
00이 몇개 들어 갈 수 있느냐로 경우의 수를 구할 수 있을듯
3 경우의 수를 보면 00이 0개 들어가면 1개, 1개 들어가면 2개
4 경우의 수를 보면 00이 0개 들어가면 1개, 1개 들어가면 3개, 2개 들어가면 1개
5 경우의 수일 때 00100 이런 경우가 있어서 단순하게 공식으로 떨어지진 않을듯
2 경우의 수와 3 경우의 수를 막무가내로 곱한다고
5 경우의 수가 나오는게 아님. why? 00이 2개와 3개 중간에 자리할 수 있으니까.
예를 들어 10011 같은 건 2의 자리에서 10이 없고 3의 자리에서 011이 없어서 안됨
아닌데? 규칙 있는 것 같다.
n // 2 만큼 00이 들어갈 수 있고,
00이 0개 있으면 경우의 수 1가지
00이 1개 있으면 경우의 수 (n+1)-2가지
00이 2개 있으면 경우의 수 ((n+1)-4)^2가지
...
00이 x개 있으면 경우의 수 ((n+1)-2x)^n
근데 이건 for문을 매번 돌려야돼서 효율이 안 좋을 뿐더러 dp도 아님.
dp로 풀라고 줬다는 건 문제가 작은 문제로 쪼개진다는 것
그리고 그것을 다시 조건으로 활용하던 더 큰 문제의 재료로 사용하던 할 수 있다는 것
그냥 (n+1)^k 를 매번 연산하지 않아도 된다는 걸 의미하는 건가? 일단 해보자
15746으로 나눠야 하는 것도 신경쓰임
15746 = 2 * 7873 임. 딱히 의미 없어 보임
상한을 정해주려고 한 건가? 계속 커지지 말라고?
N = int(input())
# 최대 00 개수
max_zero = N // 2
result = 0
def all_power(zero_n,case):
global result
global N
result += case
if zero_n < max_zero:
case
all_power(zero_n+1,case)
else:
return
print(all_power(1,N-1)+1)00이 x개 있는 경우의 수와 x+1개 있는 경우의 수는
곱하기 띡 한다고 다음 경우의 수가 나오는 관계가 아니다
로직을 다시 짜야 될듯
설마 저번에 풀었던 나머지로 나머지 계산하는 로직을 갖다 써야 되는 건가?
그건 너무 too much인듯
(n+1)-2x에 15746 나눠줘서 상한을 만들어주는 것도 생각해봤는데,
어차피 15745^3 정도만 돼도 급격하게 연산량이 증가하지 않을까?
그렇게 매번 나눠줘야 하는 건가?
동적 프로그래밍에서 자꾸 사고가 멀어지는 것 같다
1들에 00을 넣는게 아니라 00 사이에 1들을 넣는거라고 생각한다면?
00이 0개 있으면 경우의 수 1가지
00이 1개 있으면 경우의 수 n-2_C_2
00이 2개 있으면 경우의 수 n-4_C_3
...
00이 x개 있으면 경우의 수 n-2x_C_x
n-2x_C_x = (n-2x)! / ( (n-3x)! x! )
어지러워져버렸다. 이렇게 푸는 건 말이 안되는듯.
왜 위에랑 식이 다른 건지도 모르겠다. 둘 중 하나 틀린듯.
동적 프로그래밍은 쪼개야 하는 '큰 문제'가 무엇인지를 알아내는 것부터 힘든듯.
00이라는 허상에 매몰되지 말고
x일 때 00이 x//2만큼 들어갈 수 있으니
경우의 수 구할 땐 00을 하나로 합친다고 생각하는게 편하다.
00을 네모칸 1개로 보면
만들 n의 자리 이진수가 있을 때
00은 최대 n//2
00이 x개일 때 남은 1의 개수는 n - 2x
아까랑 똑같은 곳으로 되돌아왔다
range(n-2x,n-3x-1,-1) 을 곱하고 x!을 나눠주면
00이 x개일 때 만들 수 있는 n의 이진수
팩토리얼은 dp로 풀면 될 것 같고
range()는... 계산해야되나?
일단 코드를 그냥 짜보자
??? 생각해보니까 조합이 아니라 중복순열인데 왜 조합으로 풀고 있음? x신임?
지금 와서 생각해보면 전형적인 경우의 수 문제인데 왤케 돌아돌아 왔는지도 모르겠다.
00을 네모칸 1개로 보면
만들 n의 자리 이진수가 있을 때
00은 최대 n//2
00이 x개일 때 남은 1의 개수는 n - 2x
00이 x개일 때 가능한 경우의 수는 (x+1)^(n-2x)
마저도 아니다.
방금 구한 건 중복 순열.
내가 구해야 하는 건 중복 조합의 경우의 수.
x+1_H_n-2x = (n-x)! / ( x! * (n-2x)! )
n = 4일때
00 0개일 때 : 1개 4C4
00 1개일 때 : 3개 3C2
00 2개일 때 : 1개 2C0
n = 5일때
00 0개일 때 : 1개 5C5
00 1개일 때 : 4개 4C3
00 2개일 때 : 3개 3C2
n = 6일때
00 0개일 때 : 1개 6C6
00 1개일 때 : 5개 5C4
00 2개일 때 : 6개 4C2
00 3개일 때 : 1개 3C0우여곡절 끝에 제대로 된 공식을 찾아냈다.
근데 이걸 dp로 어떻게 품?
당장 떠오르는 건 팩토리얼 계산한 결과를
리스트에 넣어놓으면 되긴 할 것 같긴 한데
일단 짜보자
N = int(input())
fact = [1]*(N+1)
for i in range(1,N+1):
fact[i] = fact[i-1] * i
def combi(n,r):
return fact[n]//(fact[n-r] * fact[r])
result = 0
for i in range(N//2+1):
result += combi(N-i,N-2*i)
print(result%15746)테캐 1개는 통과해서 제출했더니 메모리 초과.
gpt한테 물어서 테케 받아봤는데 다른 것들은 다 됨.
근데 100000을 입력해봤더니 30초 지나도 계산이 안됨.
N = int(input())
fact = [1]*(N+1)
for i in range(1,N+1):
fact[i] = fact[i-1] * i이 부분만 따로 돌려봤더니 여기서부터 계산이 안됨.
팩토리얼이라 값이 너무 커져서 그랬던 것으로 추정됨.
아 그래서 15746을 조건으로 줬구나! 하고 무지성으로 생각도 안 하고
% 15746 적었더니 나머지가 0이 되는 것들이 있어서 0 나누기 오류 뜸
15746을 적용하는 방법이 뭐가 있을까 생각하다가
아무렇지도 않게 다음 문제로 넘어가는 사람들이 있는 것 같길래 답지를 봤다
n = int(input())
dp = [0]*(n+1)
dp[1] = 1
dp[2] = 2
for i in range(3, n+1):
dp[i] = (dp[i-1] + dp[i-2]) % 15746
print(dp[n])근데 답지 보고서 다른 사람들 보니까 이대로 푼 건 아니고 피보나치라는 규칙성을 찾아낸 거였음
나는 피보나치 수열 일반항을 유도해냈던 건가? 생각하고 15, 16 대입해봤더니 틀림.
애초에 맞는 접근마저도 아니었던 것 같음.
실제 피보나치 일반항은 루트 들어가고 난리났음.
근데 이거 백준에 제출했더니 인덱스 에러 뜸
내가 전 문제에서 풀었던 재귀 함수로 구현한 피보나치 코드 넣었더니 리커전 에러 & 해결했더니 메모리 초과 뜸.
내일 와서 구현해봐야할듯.
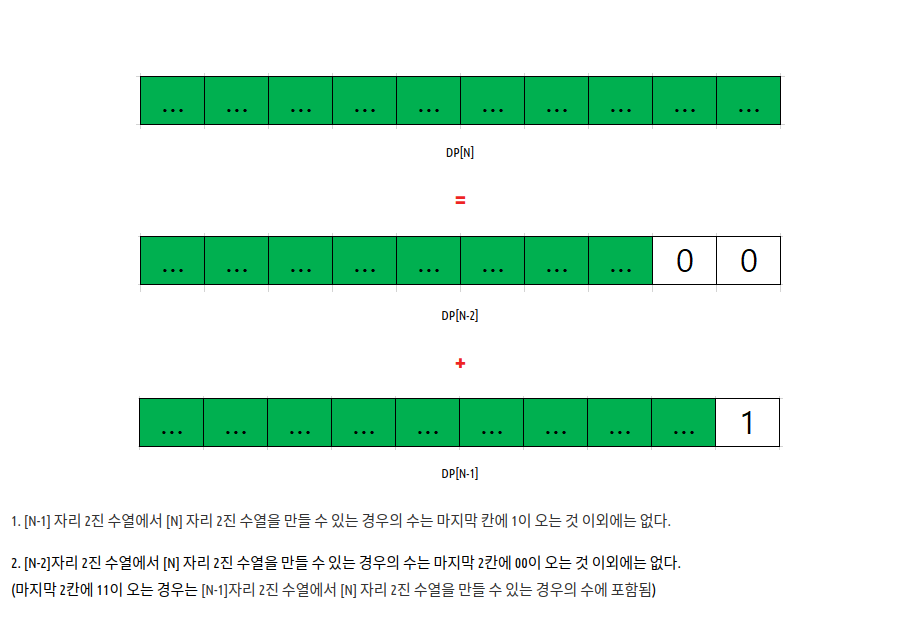
이거 보고 바로 이해함.
