🎯 To-do List
✅ 이번주차 백준 하, 중 문제 다 풀기 | 11047 동전 0, 1541 잃어버린 괄호, 1931 회의실 배정, 1946 신입사원,
☑️ 이번주차 백준 하, 중 문제 다 풀기 | 11049 행렬 곱셈 순서, 11053 가장 긴 증가하는 부분 수열
☑️ CSAPP 저자 직강 유튜브 보기
☑️ 운영체제 영상 보기
☑️ 운영체제 블로그 보기
📝 배운 것들
🏷️ 배낭 문제 (1차원 배열)
import sys
input = sys.stdin.readline
# N = 물품의 수, K = 배낭 용량
N, K = map(int, input().split())
objs = [tuple(map(int, input().split())) for _ in range(N)]
# dp[i]는 i 무게에서의 최대 가치를 저장합니다
dp = [0] * (K + 1)
# 각 물건의 무게와 가치를 가져옵니다
for weight, value in objs:
# 역순으로 순회하여 중복 사용을 방지합니다
for j in range(K, weight - 1, -1):
dp[j] = max(dp[j], dp[j - weight] + value)
print(dp[K])각 물건에 대해 순회를 하고 이제까지 구한 최적의 가치와 비교하는 것은
2차원 배열을 사용할 때와 동일하다.
하지만 최적의 물건 가치를 매번 같은 배열에 저장하므로
역으로 순회하여 중복(같은 물건을 2번 넣는 일)이 발생하지 않도록 한다.
역으로 순회한다는게 처음 보면 이해가 안될수도 있는데,
사실 2차원 배열을 쓸 때도 역으로 순회해도 문제가 똑같이 풀린다.
2차원 배열을 쓰는 것은 이해의 편의를 직관적으로 돕기 위한 장치일 뿐이다.
이전까지의 최적 가치와 현재 물건을 넣어본 가치를
비교할 때 어느 위치에서 무슨 정보를 가져오는지,
왜 역으로 순회해야 중복이 방지되는지,
이 2가지를 이해하면 1차원 배열 풀이를 이해할 수 있을 것이다.
-
초기 상태:
dp배열은 모든 값이 0으로 초기화됩니다.dp[0]부터dp[K]까지 모든 값은 처음에 0입니다.
-
역순 순회:
- 각 물품에 대해 배낭의 용량을 역순으로 순회합니다.
- 역순으로 순회하기 때문에 현재 물품을 추가하기 전의 값들이 유지됩니다.
-
값 갱신:
dp[j] = max(dp[j], dp[j - weight] + value)식을 사용하여 값을 갱신합니다.dp[j - weight]는 이미 이전 물품들을 고려하여 계산된 값입니다. 따라서dp[j - weight] + value는 현재 물품을 포함한 최대 값을 의미합니다.
입력이 다음과 같을 때:
4 10
1 1
4 8
3 6
5 12초기 dp 배열: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
-
첫 번째 물품 (무게 1, 가치 1)을 처리:
dp배열을 역순으로 갱신:dp[10] = max(dp[10], dp[10-1] + 1) = max(0, 0 + 1) = 1dp[9] = max(dp[9], dp[9-1] + 1) = max(0, 0 + 1) = 1- ...
dp[1] = max(dp[1], dp[1-1] + 1) = max(0, 0 + 1) = 1- 결과:
[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
-
두 번째 물품 (무게 4, 가치 8)을 처리:
dp[10] = max(dp[10], dp[10-4] + 8) = max(1, 1 + 8) = 9dp[9] = max(dp[9], dp[9-4] + 8) = max(1, 1 + 8) = 9- ...
dp[4] = max(dp[4], dp[4-4] + 8) = max(1, 0 + 8) = 8- 결과:
[0, 1, 1, 1, 8, 9, 9, 9, 9, 9, 9]
-
세 번째 물품 (무게 3, 가치 6)을 처리:
dp[10] = max(dp[10], dp[10-3] + 6) = max(9, 9 + 6) = 15dp[9] = max(dp[9], dp[9-3] + 6) = max(9, 9 + 6) = 15- ...
dp[3] = max(dp[3], dp[3-3] + 6) = max(1, 0 + 6) = 6- 결과:
[0, 1, 1, 6, 8, 9, 9, 14, 15, 15, 15]
-
네 번째 물품 (무게 5, 가치 12)을 처리:
dp[10] = max(dp[10], dp[10-5] + 12) = max(15, 9 + 12) = 21dp[9] = max(dp[9], dp[9-5] + 12) = max(15, 8 + 12) = 20- ...
dp[5] = max(dp[5], dp[5-5] + 12) = max(9, 0 + 12) = 12- 결과:
[0, 1, 1, 6, 8, 12, 13, 14, 15, 20, 21]
결과적으로, 최대 용량 10에서 얻을 수 있는 최대 가치는 21입니다.
따라서, 역순으로 순회하고 dp[j]를 갱신하는 방식은 물품이 중복 사용되지 않도록 하면서 올바른 최적 값을 계산할 수 있습니다.
🏷️ 플로이드 와샬
삼중 for문으로 모든 정점을 순회하면서
"나 거쳐서 갈 수 있는 놈들 있어? 싹 다 갱신해봐"
이행적 폐쇄 (Transitive Closure)
비용 상관없이 갈 수 있느냐 없느냐만 따져보면
for k in range(n): # 나 A를 거쳐서
for i in range(n): # B 너가
for j in range(n): # C로 갈 수 있니?
if closure[i][k] and closure[k][j]:
closure[i][j] = True첫번째 for문 요소 : "나 A를 거쳐서"
두번째 for문 요소 : "B 너가"
세번째 for문 요소 : "C로 갈 수 있니?"
"나 A를 거쳐서, B 너가, C로 갈 수 있니?"
최소 비용 (Floyd-Warshall Algorithm)
최소 비용 버전으로 보면
for k in range(n): # 나 A를 거쳐서 가는게
for i in range(n): # B 너가
for j in range(n): # C로 갈 때 더 빨리 가니?
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]첫번째 for문 요소 : "나 A를 거쳐서 가는게"
두번째 for문 요소 : "B 너가"
세번째 for문 요소 : "C로 갈 때 더 빨리 가니?"
"나 A를 거쳐서 가는게, B 너가, C로 갈 때 더 빨리 가니?"
⚔️ 백준
📌 11047 동전 0
# 더할 수 있는 동전 종류 중 가장 큰 동전 골라서 최대한 많이 넣기
# 남은 것들 중에서 최대한 더하기
# 더하다가 안되면 또 아래로 내려가기
# 재귀는 좀 애매하고 반복문으로 해야할듯
# 코인 금액 비싼것부터 최대한 넣어보기
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
coins = [int(input()) for _ in range(N)]
cnt = 0
for coin in reversed(coins):
while K - coin >= 0:
K -= coin
cnt += 1
print(cnt)정답 코드
일단 풀긴 했는데 진짜 반례가 없다고? 생각이 드는 문제.
(i ≥ 2인 경우에 Ai는 Ai-1의 배수) 라는 조건이 있었다.
이것 덕분에 반례가 없었던 것. 역시 뭔가 이상하더라.
📌 1541 잃어버린 괄호
# 괄호는 함정이고 '어떤 연산자를 먼저 할 것이냐'가 진짜 문제인듯
# 그럼 결과는 연산자의 순열?
# 최대한 큰 숫자를 만든 후에 - 씌워버리는 것이 최선의 전략
# - 붙은거 뒤에 있는 것들을 최대한 큰 양수로 만들어야 함 (+끼리 묶어버림)
# 55 - 50 + 40 + 30 - 10 + 20
# - 뒤에 나오는 + 들을 전부 묶어서 계산해버리면 될듯?
# 일단 연산자랑 숫자를 분리하는 것부터 문제
# 느려보이긴 하지만 일단 떠오르는 방법은
# 순회를 하면서 -, +를 순서대로 담는다
# -, +에 대해 쪼갠다 (re함수)처음 사고 과정
# -가 붙으면 다음 +가 나올때까지 그 합을 모았다가 결과에서 뺀다
import sys, re
input = sys.stdin.readline
ex, op = input().strip(), [0]
for e in ex:
if e == '+' or e == '-':
op.append(e)
ex = re.split(r'[\+\-]',ex)
cur, result, noMinus = 0, int(ex[0]), True
for i in range(1,len(op)):
ope = op[i]
if ope == '-':
noMinus = False
result -= cur
cur = int(ex[i])
else:
cur += int(ex[i])
if noMinus:
result += cur
else:
result -= cur
print(result)그대로 구현했는데 틀렸다고 뜸.
더 생각해봤더니 더 좋은 방법이 있어서 그걸로 품.
# 첫번째 - 앞은 다 더하고 뒤는 다 뺀다
import sys, re
input = sys.stdin.readline
ex, op = input().strip(), [0]
for e in ex:
if e == '+' or e == '-':
op.append(e)
ex = re.split(r'[\+\-]',ex)
result, noMinus = int(ex[0]), True
for i in range(1,len(op)):
ope = op[i]
if ope == '-':
noMinus = False
break
result += int(ex[i])
if not noMinus:
for j in range(i,len(op)):
result -= int(ex[j])
print(result)정답 코드
애초에 괄호를 마음대로 쓸 수 있다는 건 (-)가 있다면
뒤에 있는 모든 (+)를 (-)로 묶어줄 수 있다는 것이므로
첫번째 -가 발견되기 전까지 다 더해주고,
발견된 후에는 다 빼주면 된다.
noMinus 조건 판별 부분 빼버리면
(-)가 하나도 없을 때 마지막 숫자를 한 번 빼버리는 경우가 생김.
어떻게 해결할 방법이 있을 것 같은데 일단 갈 길이 바빠서 gpt한테 물어봄
import sys, re
input = sys.stdin.readline
ex = input().strip()
# 첫 번째 '-'를 기준으로 문자열을 나누기
parts = ex.split('-')
# 첫 번째 부분은 '+'로 구분된 숫자들을 모두 더하기
first_part = sum(map(int, parts[0].split('+')))
# 나머지 부분들은 '-'가 있든 없든 모든 숫자들을 더한 후 빼기
remaining_parts = sum(sum(map(int, part.split('+'))) for part in parts[1:])
# 결과 계산
result = first_part - remaining_parts
print(result)결과와 로직은 똑같은데 훨씬 간략하게 코드를 짰다.
사람이 읽기는 힘든듯.
n = str(input())
m = n.split('-')
answer = 0
# 첫번째는 -로 시작할 경우의 수가 있어서 따로 작업
x = sum(map(int, (m[0].split('+'))))
if n[0] == '-':
answer -= x
else:
answer += x
for x in m[1:]: # 첫번째 작업은 이미 했기때문에 인덱스 1부터 시작
x = sum(map(int, (x.split('+'))))
answer -= x
print(answer)이게 훨씬 간단하다. 첫번째가 (-)인 경우도 있어서 틀렸던 거구나.
📌 1931 회의실 배정
# 민폐를 끼친 회의에 대해 카운트가 2개 넘어가면 바꾸는 식으로? -> 겹치는 부분이 복잡할듯
# dp 배낭 문제랑 비슷한데? 근데 그리디라고 했으니까 dp는 배제해보자.
# 특정한 길이의 자가 주어질 때 나무 도막들을 겹치지 않게 배치하는 문제
# 내가 지금 이걸 안 넣은 선택이 나중에 어떤 결과가 될지 모른다는게 마음에 걸림
# 다른 거 넣으면 기존에는 안 가려지던 자리에 3개씩 들어갈 수도 있는데...
# 넣으려고 했는데 자리에 아무것도 없으면 고민없이 넣는다
# 넣으려고 했는데 자리에 나보다 시작도 빠르고 끝도 늦으면 고민없이 대체한다
# 나랑 조금만 겹치면 ... ?도저히 뭔지 모르겠어서 답지를 봤다.
회의를 최대한으로 많이 하려면 어떻게 해야할까?
- 회의 시작시간을 기준으로 가장 빠른 회의를 선택
이 경우에는 만약 회의시간이 많이 길다면 다른 회의를 선택하지 못하는 경우가 발생하므로 옳지 못하다!- 회의의 기간을 짧은 기준으로 선택
회의의 기간을 짧은 기준으로 선택한다면 시작 시간을 알지 못하고 끝시간을 알지 못함. 이렇게 sort된 배열을 확인할 때 시작시간과 종료시간이 뒤죽박죽이 된다.- 회의의 종료시간을 기준으로 가장 빠른 회의를 선택
종료시간을 기준으로 선택한다면 종료시간을 기준으로 sort하고 이렇게 sort된 배열을 순차적으로 확인하면서 1번 회의가 종료되었다면 다음 회의시간중 가장 빨리 끝나는 회의를 자동 선택하는 것이므로 옳다!
따라서 3번 방법을 선택한다.
더 찾아보니 이런 문제는 활동 선택 문제(Activity-Selection Problem) 라는 알고리즘에 속한다고 한다.
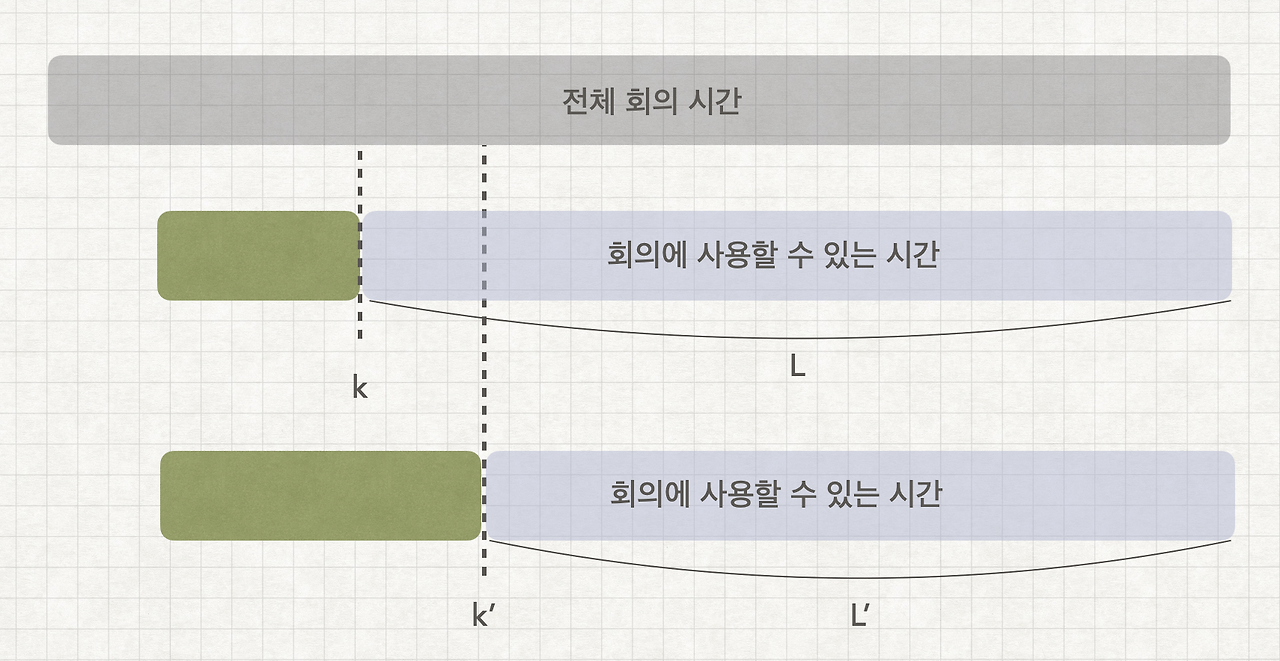
k에 끝나는 회의를 고르는것이 k'에 끝나는 회의를 고르는것보다 최적의 방법이라는 것을 반박하기 위해서는 L이라는 남은 시간보다 L'라는 남은시간에 회의들을 배치하는것이 더 많은 회의를 넣을 수 있다는 것을 증명해야한다.
과연 같은 회의목록들을 가지고 더 적은 타임에 많은 회의들을 넣는것이 가능할까?
당연히 불가능 하다.
따라서 항상 가장 빨리 끝나는 회의를 선택하는것이 최적의 해를 도출해낸다고 볼수 있다.
일단 보고 이해하긴 했는데 어느 정도는 암기를 해야될 것 같다.
문제 풀 때 확인해야할 것으로
1. 문제의 조건에 뭐가 있지?
2. 그것들로 최적의 조건을 어떻게 찾지?
3. 가장 빨리 끝나는 것이 가장 적게 차지한다
이것들을 얻어가면 될듯
import sys
input = sys.stdin.readline
N = int(input())
meets = [tuple(map(int,input().split())) for _ in range(N)]
def second_val(x):
return x[1]
meets.sort(key = second_val)
end, cnt = -1, 0
for meet in meets:
if end <= meet[0]:
cnt += 1
end = meet[1]
print(cnt)간단해서 구현해보려고 했는데 자꾸 90퍼 쯤에서 틀렸습니다! 뜸.
import sys
input = sys.stdin.readline
N = int(input())
meets = [tuple(map(int,input().split())) for _ in range(N)]
meets.sort(key=lambda x: (x[1], x[0]))
end, cnt = -1, 0
for meet in meets:
if end <= meet[0]:
cnt += 1
end = meet[1]
print(cnt)답지 봤더니 정렬을 lambda로 하고 있었음. 첫번째 수도 정렬을 해줘야 한다고 한다.
근데 왜?
종료 시각이 같은 두 회의 중, 한 회의는 시작 시각이 종료 시각보다 빠르고, 다른 회의는 시작 시각과 종료 시각이 같다면, 반드시 시작 시각이 더 빠른 회의를 먼저 선택하는 것이 이득입니다.
시작 시간이랑 종료 시간이 같은 걸 먼저 넣어버려서 종료 시간이 뒤로 밀려나면
나중에 (시작시간==종료시간)인 회의를 넣으면 2개를 넣을 수 있는데
1개만 넣게 되어버리는 경우가 생긴다.
그래서 종료 시간에 대해서 정렬 뿐만 아니라 겹치는 값들은 시작 시간으로 정렬해줘야됨.
📌 1946 신입 사원
# 1차 성적으로 sort 후에
# 왼쪽부터 하나씩 순회를 한다
# 지금까지의 2차 순위 중 최고와 비교하여 낮으면 탈락
import sys
input = sys.stdin.readline
T = int(input())
for _ in range(T):
N = int(input())
apply = []
for _ in range(N):
newbie = list(map(int,input().split()))
apply.append(newbie)
apply.sort()
best_2nd = len(apply)+1
cnt = 0
for newbie in apply:
if newbie[1] < best_2nd:
best_2nd = newbie[1]
cnt += 1
print(cnt)머릿속으로만 한참 헤매다가 지원자를 직접 나열해보니 규칙이 보였다.
근데 맞긴 했는데 시간이 너무 오래 걸림.
다른 사람 코드들도 다 오래 걸리긴 했는데 더 빠른 방법이 없나 찾아봤지만
다들 별 차이 없는듯.
📌 11049 행렬 곱셈 순서
# 제일 큰 거 2번 안 곱하게 하나씩 삭제하면 될듯
# 시간 초과 뜨면 연결 리스트로 구현해야 할듯
import sys
input = sys.stdin.readline
N = int(input())
L = []
L.extend(map(int,input().split()))
for _ in range(N-1):
L.append(list(map(int,input().split()))[1])
result = 0
for i in range(N-1):
max, max_idx = 0, 0
for j in range(1,len(L)-1):
if max < L[j]:
max, max_idx = L[j], j
result += L[max_idx-1]*L[max_idx]*L[max_idx+1]
del L[max_idx]
print(result)연산 얼마나 비싼지 생각 안 하고 일단 돌려봤는데 시간 초과도 아닌 틀렸습니다! 가 떴다.
애초에 로직 자체가 잘못됐었다.
양 끝 값이 엄청 큰데도 계속 연산하는 경우가 생겨버림.
그리디 풀다 와서 dp 문제라는 걸 까먹음.
dp로 다시 접근해보자.
그냥 답지 봄...
