📚 Journal
발표 세션 직후 질문 시간에 한 질문
Q. 근데 왜 리눅스를 쓰는 건지?
A. OS마다 컴파일러의 차이가 꽤 있음
Q. 꼭 Ubuntu 특정 버전을 써야 하는지?
A. 나중에 PintOS 때 문제될 수 있는데 그건 나중에 얘기할 것.
코치님과 점심 중 QnA
발표 세션이 끝나고 코치님이 동기들이 다같이 점심 먹는 자리에 함께해주셨다.
Q. 나만무 프로젝트 때 싱글 게임은 멀티 게임에 비해 코치분들이 흡족해하지 않으시는지?
A. (코치님) 아무래도 싱글 게임은 기술 스택 쓸 게 없다보니까 멀티 게임이 보통 나을듯. 그리고 그런 기술적 부분이 없으면 코치분들이 아니라 실제 취업할 때 면접관들이 흡족해하시지 않으실 것.
Q. 유니티 튜토리얼 끝내도 어떻게 아이디어를 구현할지 떠오르질 않아서 항상 상상 기획만 했다
A. (동기분) 유니티 Docs나 디자인 패턴같은거 익혀볼것
Q. 아무것도 못하는데 그냥 팀에 일단 들어가보는게 나을지
A. (동기분) 옛날 게임들 소스 코드 보면서 구현해보고 (1~2달 소요) 참가해볼것. 모교의 관련 학과나 동아리나 대학 연합 동아리, 인디터, 인디라 등에서 팀 구할 수 있을 것.
Q. 비전공자여도 보통 1~2년 지나면 따라잡긴 하는지? (바보같은 질문이긴 한데 그냥 해봄)
A. (코치님) 자신의 머릿속에 지식을 얼마나 쌓았는지에 따라 달릴 것
Q. 끝나고 못 풀었던 문제 메꾸거나 제대로 못봤던 책같은 것들 복습하는게 좋을지?
A. (코치님) 일단 취업 준비가 우선. 취업에 필요한거 먼저 하는게 맞음.
Q. 서버쪽은 직종(게임, 웹 등) 간의 이직이 비교적 자유로운지?
A. (코치님) 서버가 다른 직무보다 특별히 더 이직을 잘한다 같은건 없음. 일하면서 다른 거 많이 해봤으면 이직에 도움될 것. 자신은 서버 데이터 보다보니 자연스럽게 데이터 사이언스 쪽으로 갈 수 있었음. 그런 느낌의 케바케.
Q. 요즘도 개발자는 40대 이상이면 상위 1% 아니면 힘든가?
A. (코치님) 일반론으로 접근하자면 매니저나 디렉터 쪽으로 빠지긴 함. 근데 일단 자신은 현업으로 하고 있음.
📝 배운 것들
🏷️ 주소값이 필요할 때 포인터 변수 대신 &
void reverse(Queue *q)
{
// 큐에서 데이터 빼서 스택에 담은 다음 큐에 다시 담아라~
Stack *rS;
rS = (Stack *)calloc(1,sizeof(Stack));
// rS->ll.size = 0; <- malloc으로 바꾸면 이거 추가
while(!(isEmptyQueue(q))){
push(rS, dequeue(q));
}
while(!(isEmptyStack(rS))){
enqueue(q, pop(rS));
}
free(rS);
}곧이 곧대로 포인터 변수 만든 다음에 malloc하는게 아니라
void reverse(Queue *q)
{
Stack s;
s.ll.head = s.ll.tail = NULL;
s.ll.size = 0;
int num = 0;
//큐에있는걸 다 스택에 넣음
while(q->ll.size != 0){
num = dequeue(q);
push(&s, num);
}
//스택에 있는걸 다 큐에 넣음
while(s.ll.size != 0){
num = pop(&s);
enqueue(q, num);
}
return;
}스택 만든 다음에 &s 하면 주소값 쓸 수 있음
📦 레드 블랙 트리 개념 정리
https://www.youtube.com/watch?v=2MdsebfJOyM
이 영상 보고 정리한 내용
개념과 속성
개념
- 이진 탐색 트리(BST)의 한 종류
- 스스로 균형(balancing) 잡는 트리
- BST의 worst case의 단점을 개선
- 모든 노드는 red 혹은 black
속성
#1 : 모든 노드는 red 혹은 black
#2 : 루트 노드는 black
#3 : 모든 nil(leaf) 노드는 black
#4 : red의 자녀들은 black (= red가 연속적으로 존재할 수 없다)
#5 : 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다 (자기 자신은 카운트에서 제외)
nil 노드란?
- 존재하지 않음을 의미하는 노드
- 자녀가 없을 때 자녀를 nil 노드로 표기
- 값이 있는 노드와 동등하게 취급
- RB 트리에서 leaf 노드는 nil 노드
노드 x의 black height
- 노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black 수 (자기 자신은 카운트에서 제외)
#5속성을 만족해야 성립하는 개념
색을 바꾸면서도 #5 속성을 유지하기
RB 트리가 #5 속성을 만족하고 있고
두 자녀가 같은 색을 가질 때
부모와 두 자녀의 색을 바꿔줘도
#5 속성은 여전히 만족한다
#5 : 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다
RB 트리는 어떻게 균형을 잡는가?
삽입/삭제 시 주로 #4, #5를 위반하며
이들을 해결하려고 구조를 바꾸다 보면
자연스럽게 트리의 균형이 잡히게 된다
#4 : 노드가 red라면 자녀들은 black
#5 : 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다
삽입
Overview
- 삽입 전 RB 트리 속성 만족한 상태
- 삽입 방식은 일반적인 BST와 동일
- 삽입 후 RB 트리 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
과정
삽입하는 노드는 항상 red다
1.
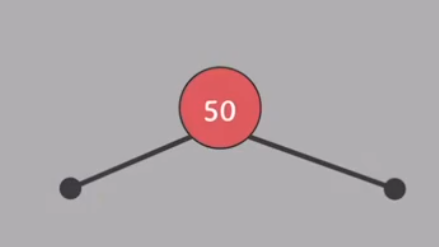
빈 트리에 50을 삽입한다
두 nil 노드의 색은 black으로 고정한다
그러면 자연스럽게 #3 속성을 만족
#3 : 모든 nil 노드는 black
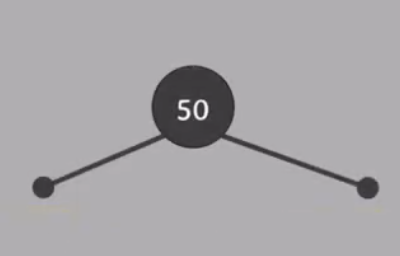
하지만 RB 트리 #2 속성 위반
루트 노드를 black으로 바꾸면 해결
#2 : 루트 노드는 black
red 삽입 후
#2속성을 위반했을 때 해결법루트 노드를 black으로 바꿔준다
2.
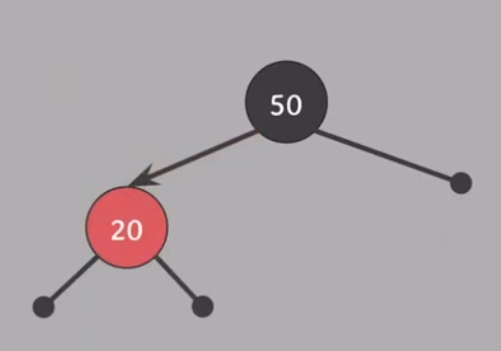
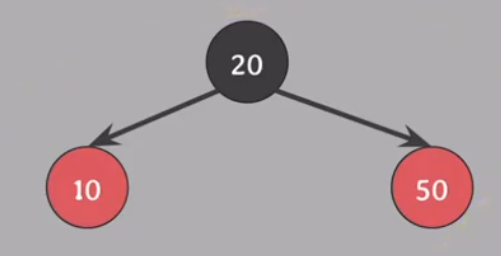
20을 삽입한다
BST 속성에 따라 왼쪽 노드에 연결하면
RB 트리의 모든 속성을 만족
왜 새로 삽입하는 노드는 red인가?
삽입 후에도
#5속성을 만족하기 위해
#5: 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다
3.
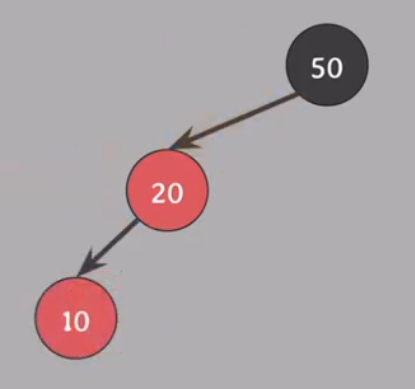
10을 삽입한다.
#4를 위반한다.
#4 : 노드가 red라면 자녀들은 black
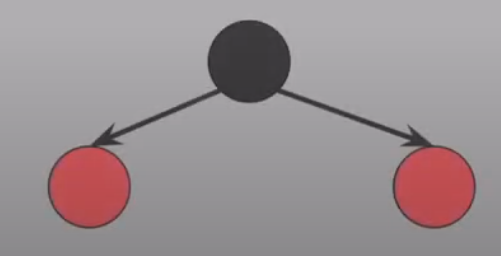
이를 어떻게 해결할까?
red가 한 쪽으로 몰려 있으니
red 하나를 반대편으로 옮겨준다면?
구조를 바꾸면서도 BST의 특징을 유지시키는 방법은
회전이다
#4 속성 위반을 해결하기 위해
red 하나를 넘겨야 하는데
BST 특징 또한 유지하면서 넘기려면
회전을 사용해야 한다
회전을 어떻게 사용할지가 관건이다
#4 : 노드가 red라면 자녀들은 black
- 20과 50의 색을 바꿔준다
- 50을 기준으로 오른쪽을 회전한다
이렇게 되면 #4 속성을 포함해서 RB 트리 속성들을 모두 만족
#1 : 모든 노드는 red 혹은 black
#2 : 루트 노드는 black
#3 : 모든 nil 노드는 black
#4 : 노드가 red라면 자녀들은 black
#5 : 각 노드에서 자손 nil 노드들까지 가는 모든 경로는 black 수가 같다
삽입 후
#4속성을 위반했을 때 case.3 해결법case.3
삽입된 red 노드가 부모의 왼쪽 자녀
& 부모도 red고 할아버지의 왼쪽 자녀
& 삼촌(=부모의 형제)은 black이라면부모와 할아버지의 색을 바꾼 후
할아버지 기준으로 오른쪽으로 회전한다
- 오른쪽 왼쪽을 바꿔도 성립
삽입 후
#4속성을 위반했을 때 case.2 해결법case.2
삽입된 red 노드가 부모의 오른쪽 자녀
& 부모도 red고 할아버지의 왼쪽 자녀
& 삼촌(=부모의 형제)은 black이라면부모를 기준으로 왼쪽으로 회전한 뒤
할아버지 기준으로 오른쪽으로 회전한다
- 오른쪽 왼쪽을 바꿔도 성립
삽입 후
#4속성을 위반했을 때 case.1 해결법case.1
삽입된 red 노드의 부모도 red
& 삼촌(=부모의 형제)도 red라면부모와 삼촌을 black으로 바꾸고
할아버지를 red로 바꾼 뒤
할아버지에서 다시 확인을 시작한다
삭제
Overview
- 삭제 전 RB 트리 속성 만족한 상태
- 삭제 방식은 일반적인 BST와 동일
- 삭제 후 RB 트리 속성 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
삭제하려는 노드의 (nil이 아닌) 자녀가 없거나 하나라면
: 삭제되는 색 = 삭제되는 노드의 색
삭제하려는 노드의 (nil이 아닌) 자녀가 둘이라면
: 삭제되는 색 = 삭제되는 노드의 successor의 색
삭제되는 색을 통해 속성 위반 여부를 확인함
RB 트리에서 노드를 삭제할 때 어떤 색이 삭제되는지가 속성 위반 여부를 확인할 때 매우 중요
삭제되는 색이 red라면 어떠한 속성도 위배하지 않는다.
삭제되는 색이 black이라면#2,#4,#5속성을 위반할 수 있다.
#2 : 루트 노드는 black
#4 : 노드가 red라면 자녀들은 black
#5 : 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black 수는 같다
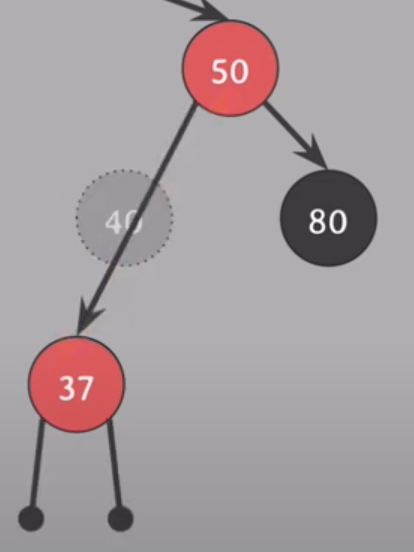
#4, #5 위배
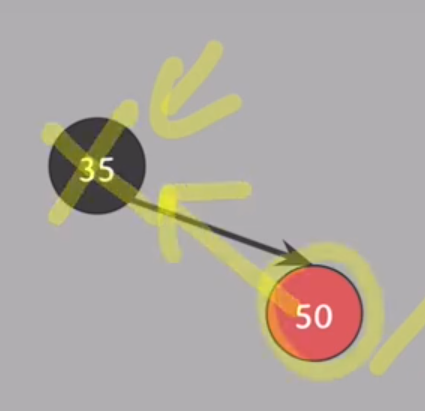
#1 위배
삭제되는 색이 black일 때 특수한 상황을 제외하면
#5속성을 항상 위반하게 된다
#5: 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black 수는 같다
삭제되는 색이 black이고 #5 위반일 때
#5 속성을 다시 만족시키기 위해
삭제된 색의 위치를 대체한 노드에
extra black을 부여한다.
extra black
경로에서 black 수를 카운트할 때
하나의 black으로 카운트된다.
nil 노드에 extra black이 부여되면 : doubly black
red 노드에 extra black이 부여되면 : red-and-black
extra black 부여 후 doubly 블랙 해결하기
네 가지 case로 분류할 때의 기준은 doubly black의 형제의 색과 그 형제의 자녀들의 색
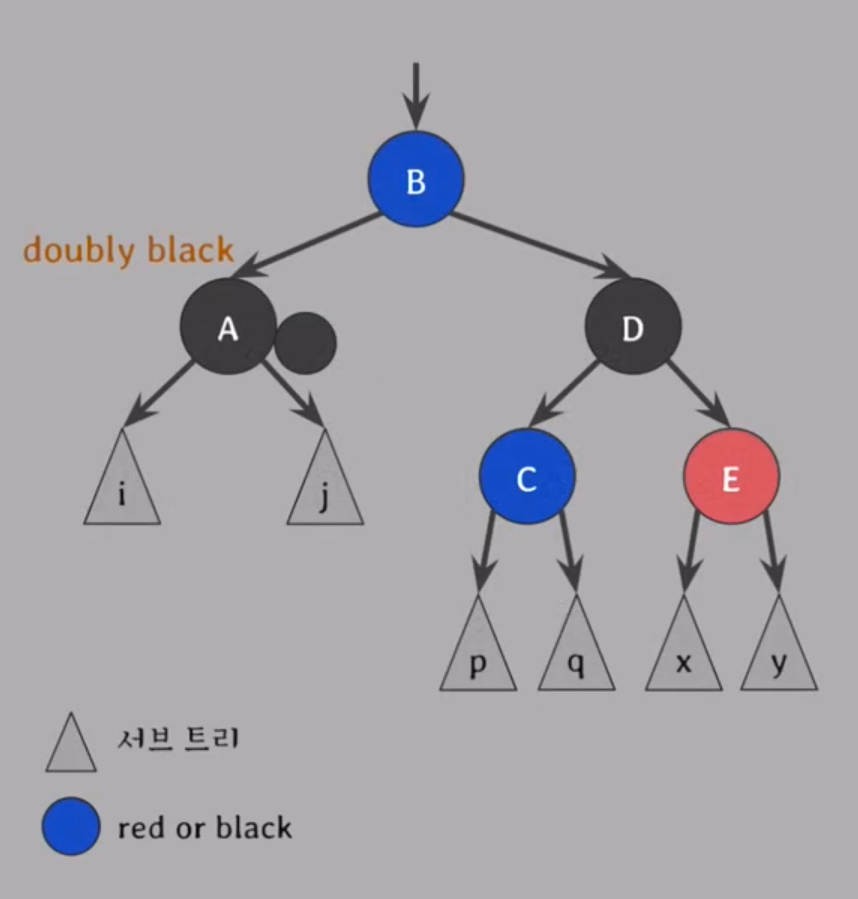
doubly black의 오른쪽 형제가 black
& 그 형제의 오른쪽 자녀가 red일 때
오른쪽 형제는 부모의 색으로,
오른쪽 형제의 오른쪽 자녀는 black으로,
부모는 black으로 바꾼 후에
부모를 기준으로 왼쪽으로 회전하면
