📦 Red-black tree
📌 rbt 과제 VSCode로 디버깅 하는 방법
📌 버그 났던 부분 1
책에 있는 슈도 코드 따라서 구현해보는 식으로 진행했었는데
오류 점검이 책에 있는걸 그대로 따라쳤나 안 쳤나 하는 식의 오타 점검이 되어버림
버그가 도저히 찾아지질 않고 어차피 이해도 제대로 하려고도 했었기에 주석을 일일이 달아봤는데
문제가 되는 부분을 바로 찾았다.
insert_fix에서
z의 부모가 z의 조부모가 오른쪽 자식이었다면
z가 부모의 왼쪽 자식일 때 오른쪽 회전을 먼저 해줘야 하는건데
잘못 적어놨었음
효율도 좋지만 무지성은 자제하자
더 늦어진다
📌 버그 났던 부분 2

delete_fix에서
조건에 괄호를 안 달아줬고, 좌우반전된 부분에서 left를 right로 잘못 적어놓음
맨 마지막 BLACK도 안 써놨었음
📌 버그 났던 부분 3
while (x != t->nil) // 리프 노드를 찾을때까지
{
y = x; // y는 최종적으로 리프 노드가 될 것
x = (z->key < x->key) ? x->left : x->right; // x는 최종적으로 리프 노드의 자식이 될 것
}
z->parent = y; // 넣을 노드의 부모를 리프 노드로 변경
if (y == t->nil) // 탐색이 바로 종료됐다면 루트에 노드 넣기
{
t->root = z;
}
else if (z->key < y->key) // 넣을 노드가 부모 노드보다 작다면
{
y->left = z; // 넣을 노드는 부모 노드의 왼쪽 자식
}
else // 넣을 노드가 부모 노드보다 크다면
{
y->right = z; // 넣을 노드는 부모 노드의 오른쪽 자식
}x = (z->key < x->key) ? x->left : x->right; 이 부분에는 (z->key < x->key) 이렇게 잘 써놓고
else if (z->key < y->key) 이 부분에는 (z->key <= x->key) 이렇게 써놨었다. 그래서 안 들어가는 경우가 생겼음. 근데 test_find_erase_rand(10000, 55); 일때는 되고 test_find_erase_rand(1000000, 55); 일때는 안됐다. 원인은 알아낼 방도를 모르겠어서 ㅈㅈ...
📌 완성 코드
#include "rbtree.h"
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
///////////////////////// function prototypes ////////////////////////////////////
// 메모리: 트리 생성/삭제
rbtree *new_rbtree(void);
void delete_rbtree(rbtree *);
// 좌회전, 우회전
void right_rotate(rbtree *t, node_t *y);
void left_rotate(rbtree *t, node_t *x);
// 위치 바꾸기
void rb_transplant(rbtree *t, node_t *u, node_t *v);
// 노드 삽입/삭제
node_t *rbtree_insert(rbtree *t, const key_t);
int rbtree_erase(rbtree *t, node_t *z);
// 삽입/삭제 fixup
void rb_insert_fixup(rbtree *t, node_t *z);
void rb_erase_fixup(rbtree *t, node_t *x);
// 노드 검색
node_t *rbtree_find(const rbtree *, const key_t);
node_t *rbtree_min(const rbtree *);
node_t *rbtree_max(const rbtree *);
// 노드에서부터 찾기
node_t *min_from_node(rbtree *t, node_t *x);
node_t *max_from_node(rbtree *t, node_t *x);
// 트리를 배열로 변환 -> inorder traversing으로 구현!!!
// traversing 순서: node, node->left, node->right
int rbtree_to_array(const rbtree *, key_t *, const size_t);
void inorder(const rbtree *t, key_t *arr, size_t *index, node_t *x, const size_t n);
//////////////////////////////////////////////////////////////////////////
rbtree *new_rbtree(void)
{
// TODO: initialize struct if needed
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
p->nil = malloc(sizeof(node_t));
p->nil->color = RBTREE_BLACK;
p->nil->left = p->nil->right = p->nil->parent = NULL;
p->root = p->nil;
return p;
}
void left_rotate(rbtree *t, node_t *x)
{
node_t *y = x->right; // y는 x의 오른쪽 자식
x->right = y->left; // x에게 y의 왼쪽 자식 떼어서 주기
if (y->left != t->nil) // y의 왼쪽 자식이 nil이 아니라면
{
y->left->parent = x; // y의 왼쪽 자식의 부모 변경
}
y->parent = x->parent; // x의 부모를 y의 부모로 바꿔줌
if (x->parent == t->nil) // x가 루트였다면
{
t->root = y; // y도 루트로 바꿔주기
}
else if (x == x->parent->right) // x가 부모의 오른쪽 자식이었다면
{
x->parent->right = y; // y도 부모의 오른쪽 자식
}
else // x가 부모의 왼쪽 자식이었다면
{
x->parent->left = y; // y도 부모의 왼쪽 자식
}
y->left = x; // y->x 연결
x->parent = y; // x->y 연결
}
void right_rotate(rbtree *t, node_t *y)
{
node_t *x = y->left; // x는 y의 왼쪽 자식
y->left = x->right; // y에게 x 자식 떼어서 주기
if (x->right != t->nil) // x의 자식이 nil이 아니었다면
{
x->right->parent = y; // x의 자식의 부모 변경
}
x->parent = y->parent; // x의 부모를 y의 부모로 바꿔줌
if (y->parent == t->nil) // y가 루트였다면
{
t->root = x; // x를 루트로 바꿔줌
}
else if (y == y->parent->left) // y가 부모의 왼쪽 자식이었다면
{
y->parent->left = x; // x도 부모의 왼쪽 자식
}
else // y가 부모의 오른쪽 자식이었다면
{
y->parent->right = x; // y도 부모의 왼쪽 자식
}
x->right = y; // x->y 연결
y->parent = x; // y->x 연결
}
void rb_transplant(rbtree *t, node_t *u, node_t *v)
{
// u 자리에 v 넣는 함수
if (u->parent == t->nil) // u가 루트라면
{
t->root = v; // 루트 자리에 v를 복사해서 넣는다
}
else if (u == u->parent->left) // u가 부모의 왼쪽 자식이라면
{
u->parent->left = v; // u 자리에 v를 복사해서 넣는다
}
else // u가 부모의 오른쪽 자식이라면
{
u->parent->right = v; // u 자리에 v를 복사해서 넣는다
}
v->parent = u->parent; // v의 부모를 u의 부모로 바꿔준다
}
void delete_rbtree_recursive(rbtree *t, node_t *node)
{
if (node == t->nil)
return;
delete_rbtree_recursive(t, node->left);
delete_rbtree_recursive(t, node->right);
free(node);
}
void delete_rbtree(rbtree *t)
{
// TODO: reclaim the tree nodes's memory
delete_rbtree_recursive(t, t->root);
free(t->nil);
free(t);
}
node_t *rbtree_insert(rbtree *t, const key_t key)
{
// TODO: implement insert
node_t *y = t->nil; // nil로 초기화
node_t *x = t->root; // 루트에서 탐색 시작
node_t *z = (node_t *)malloc(sizeof(node_t)); // 넣을 노드 z 선언
z->key = key;
while (x != t->nil) // 리프 노드를 찾을때까지
{
y = x; // y는 최종적으로 리프 노드가 될 것
x = (z->key < x->key) ? x->left : x->right; // x는 최종적으로 리프 노드의 자식이 될 것
}
z->parent = y; // 넣을 노드의 부모를 리프 노드로 변경
if (y == t->nil) // 탐색이 바로 종료됐다면 루트에 노드 넣기
{
t->root = z;
}
else if (z->key < y->key) // 넣을 노드가 부모 노드보다 작다면
{
y->left = z; // 넣을 노드는 부모 노드의 왼쪽 자식
}
else // 넣을 노드가 부모 노드보다 크다면
{
y->right = z; // 넣을 노드는 부모 노드의 오른쪽 자식
}
z->left = t->nil; // z의 자식들은 nil로 초기화
z->right = t->nil;
z->color = RBTREE_RED;
rb_insert_fixup(t, z);
return z;
}
void rb_insert_fixup(rbtree *t, node_t *z)
{
// 넣었던 노드 z의 부모가 빨강이라면, fix를 해줘야됨
while (z->parent->color == RBTREE_RED)
{
// z의 부모가 z의 조부모의 왼쪽 자식이었다면
if (z->parent == z->parent->parent->left)
{
// z의 삼촌 y 지정
node_t *y = z->parent->parent->right;
// z의 삼촌의 색깔이 빨강이었다면
if (y->color == RBTREE_RED)
{
z->parent->color = RBTREE_BLACK; // z의 부모와
y->color = RBTREE_BLACK; // z의 삼촌의 색깔을 검은색으로,
z->parent->parent->color = RBTREE_RED; // z의 조부모의 색은 빨강으로 만듬
z = z->parent->parent; // z의 조부모에 대해 다시 fix 시도
}
// z의 삼촌의 색깔이 검정이었다면
else
{
// z가 부모의 오른쪽 자식이라면
if (z == z->parent->right)
{
z = z->parent; // z에 부모 노드를 지정해준 뒤
left_rotate(t, z); // 부모에 대해 왼쪽 회전
}
z->parent->color = RBTREE_BLACK; // z의 부모의 색깔을 검은색으로 바꿈
z->parent->parent->color = RBTREE_RED; // z의 조부모의 색깔을 빨강으로 바꿈
right_rotate(t, z->parent->parent); // z의 조부모에 대해 우측 회전
}
}
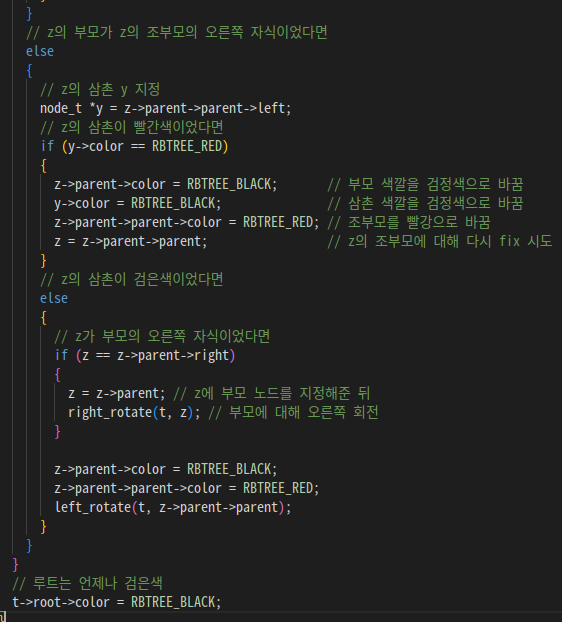
// z의 부모가 z의 조부모의 오른쪽 자식이었다면
else
{
// z의 삼촌 y 지정
node_t *y = z->parent->parent->left;
// z의 삼촌이 빨간색이었다면
if (y->color == RBTREE_RED)
{
z->parent->color = RBTREE_BLACK; // 부모 색깔을 검정색으로 바꿈
y->color = RBTREE_BLACK; // 삼촌 색깔을 검정색으로 바꿈
z->parent->parent->color = RBTREE_RED; // 조부모를 빨강으로 바꿈
z = z->parent->parent; // z의 조부모에 대해 다시 fix 시도
}
// z의 삼촌이 검은색이었다면
else
{
// z가 부모의 왼쪽 자식이었다면
if (z == z->parent->left)
{
z = z->parent; // z에 부모 노드를 지정해준 뒤
right_rotate(t, z); // 부모에 대해 오른쪽 회전
}
z->parent->color = RBTREE_BLACK; // z의 부모의 색깔을 검은색으로 바꿈
z->parent->parent->color = RBTREE_RED; // z의 조부모의 색깔을 빨강으로 바꿈
left_rotate(t, z->parent->parent); // z의 조부모에 대해 좌측 회전
}
}
}
// 루트는 언제나 검은색
t->root->color = RBTREE_BLACK;
}
node_t *rbtree_find(const rbtree *t, const key_t key)
{
// TODO: implement find
node_t *f = t->root;
while (f != t->nil && f->key != key)
{
if (key < f->key)
{
f = f->left;
}
else
{
f = f->right;
}
}
if (f == t->nil)
{
return NULL;
}
return f;
}
node_t *rbtree_min(const rbtree *t)
{
// TODO: implement find
node_t *x = t->root;
while (x->left != t->nil)
{
x = x->left;
}
return x;
}
node_t *rbtree_max(const rbtree *t)
{
node_t *x = t->root;
while (x->right != t->nil)
{
x = x->right;
}
return x;
}
node_t *min_from_node(rbtree *t, node_t *x)
{
while (x->left != t->nil)
{
x = x->left;
}
return x;
}
int rbtree_erase(rbtree *t, node_t *z)
{
// TODO: implement erase
node_t *x; // 지워진 노드 저장하는 변수
node_t *y = z; // 지울 노드 저장하는 변수
color_t y_original_color = y->color; // 지울 노드의 원래 색깔 저장해놓기
if (z->left == t->nil) // 지울 노드의 왼쪽 자식이 nil이라면
{
x = z->right; // 지울 노드의 오른쪽 자식 저장해두고
rb_transplant(t, z, z->right); // 지울 노드 자리에 지울 노드의 오른쪽 자식 넣기
}
else if (z->right == t->nil) // 지울 노드의 오른쪽 자식이 nil이라면
{
x = z->left; // 지울 노드의 왼쪽 자식 저장해두고
rb_transplant(t, z, z->left); // 지울 노드 자리에 지울 노드의 왼쪽 자식 넣기
}
else // z의 자식이 둘 다 있다면
{
y = min_from_node(t, z->right); // 후임자 찾아서 y로 지정
y_original_color = y->color; // 많은 사람들이 자신의 문제와 해결책을 공유하는 것은 강력하다.후임자의 원래 색깔 저장해놓기
x = y->right; // 후임자의 오른쪽 자식 저장해두고
if (y->parent == z) // 후임자의 부모가 z라면
{
x->parent = y; // 후임자의 오른쪽 자식의 부모는 y
}
else // 후임자의 부모가 z가 아니라면
{
rb_transplant(t, y, y->right); // 후임자와 후임자의 오른쪽 자식의 자리를 바꿈
y->right = z->right; // 후임자에게 지울 노드의 자식 물려주기
y->right->parent = y; // 물려받은 자식의 부모 갱신하기
}
rb_transplant(t, z, y); // z와 y의 위치 바꾸기
y->left = z->left; // y에게 z의 왼쪽 자식 물려주기
y->left->parent = y; // 물려받은 자식의 부모 갱신하기
y->color = z->color; // y의 색깔을 z의 색깔로 바꾸기
}
free(z);
if (y_original_color == RBTREE_BLACK)
{
rb_erase_fixup(t, x);
}
return 0;
}
void rb_erase_fixup(rbtree *t, node_t *x)
{
node_t *w;
while (x != t->root && x->color == RBTREE_BLACK)
{
if (x == x->parent->left)
{
w = x->parent->right;
if (w->color == RBTREE_RED)
{
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right;
}
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK)
{
w->color = RBTREE_RED;
x = x->parent;
}
else
{
if (w->right->color == RBTREE_BLACK)
{
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root;
}
}
else
{
w = x->parent->left;
if (w->color == RBTREE_RED)
{
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left;
}
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK)
{
w->color = RBTREE_RED;
x = x->parent;
}
else
{
if (w->left->color == RBTREE_BLACK)
{
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n)
{
size_t index = 0; // 인덱스를 0으로 초기화
inorder(t, arr, &index, t->root, n); // 인덱스의 주소와 n을 전달
return 0;
}
void inorder(const rbtree *t, key_t *arr, size_t *index, node_t *x, const size_t n)
{
if (x != t->nil)
{
inorder(t, arr, index, x->left, n);
if (*index < n)
{ // 배열의 크기를 초과하지 않도록 확인
arr[*index] = x->key;
(*index)++;
}
inorder(t, arr, index, x->right, n);
}
}