크래프톤 정글 TIL : 0920

lazyArtisan·2024년 9월 20일

TIL

정글 TIL

목록 보기

82/147

📝 배운 것들

🏷️ O(VE) 의미

V는 정점 개수, E는 간선 개수

🏷️ 다익스트라 알고리즘

1. 기초

가중치가 있는 그래프에서
한 정점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘

이해하기 쉬운 설명

매 단계마다 도달할 수 있는 정점 중에서
시작점으로부터의 거리가 가장 가까운 정점을 구하고,
해당 거리를 확정한다.
거리가 확정되면 해당 정점과 연결된 정점들의 거리도 갱신해준다.

'dp + 그리디'로 이해하면 된다.
다익스트라는 "항상 최소만 찾는 미친놈"이다.

간단하게 생각하여,
매 순간마다 최소 거리인 놈들을 확정하면
최소 거리가 아닌 정보가 있을 수 없다.

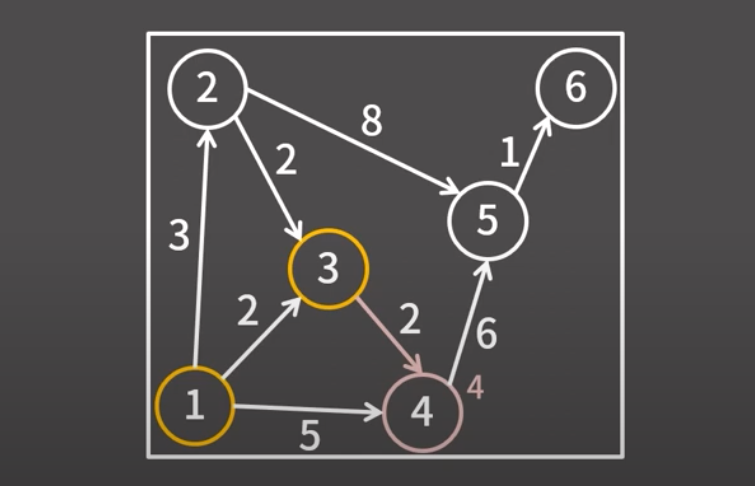
1번째로 탐색하는 정점은 자기 자신이니까 거리가 0인게 자명.
2번째로 탐색하는 정점은 자기 자신으로부터 직접 이어진 정점이니까 최소 거리인게 자명.

3번째로 탐색하는 정점이 2번째 정점과 이어져있다면
기존에 저장돼있던 (1번 ~ 3번)의 가중치와 (2번 ~ 3번) 간선 중 최솟값을 저장하고 최소 거리 확정.

하필 (1번 ~ 3번) 과 (2번 ~ 3번)의 가중치가 너무 커서
(1번 ~ A번 ~ B번 ~ C번 ~ 3번)의 거리가 더 작을수도 있는거 아니냐고?

그러면 A번 정점을 고르지 3번 정점을 고를 수가 없음. (음수 간선이 있지 않는 한)
3번 정점을 골랐다는 말은, A번 정점은 그것보다 더 큰 가중치를 가졌다는 말임.

2. 시간 복잡도

V : 정점(노드) 개수
E : 간선(엣지) 개수

간단한 배열 사용 : O(V^2)

방문하지 않은 정점 중 시작점에서 가장 가까운 정점을 찾기 위해
시작점에서 모든 정점까지의 최소 거리를 일일이 탐색하면
매번 최단 거리를 구하는 데 O(V)의 시간이 걸리고,
이를 모든 정점에 대해 반복하면 O(V^2)

우선순위 큐 사용 : O((E+E) log V)

인터넷 설명들은 O((E+V) log V)로 나와있는데 구현은 O((E+E) log V)로 다르게 돼있다고 함.

'다익스트라 알고리즘은 그리디 알고리즘이기 때문에 A->C(비용+4) 대신 A->B(비용+3)을 선택 후 B를 방문처리하게 된다. 현재는 나쁘지만 미래에는 좋은 결과를 불러오는 A->C(비용+4)&C->B(비용-5) 경로(비용-1)를 선택하지 않게 되고 올바른 해를 도출할 수 없게 된다'라는 설명은 이 구현에서는 들어맞지 않게 된다.

3. 우선순위 큐를 이용한 다익스트라 (실제 구현)

우선순위 큐에 (0, 시작점) 추가
우선순위 큐에서 거리가 가장 작은 원소를 선택, 해당 거리가 최단 거리 테이블에 있는 값과 다를 경우 넘어감
원소가 가리키는 정점을 V라고 할 때, V와 이웃한 정점들에 대해 최단 거리 테이블 값보다 V를 거쳐가는 것이 더 작은 값을 가질 경우 최단 거리 테이블의 값을 갱신하고 우선순위 큐에 (거리, 이웃한 정점의 번호)를 추가
우선순위 큐가 빌 때까지 2, 3번 과정을 반복

이전에 최소값만 찾는 미친놈 모드에서 살짝 순해진 대신 시간 복잡도 낮아진다.
최소가 갱신되면 우선순위 큐에 정점을 추가한다. 이외엔 똑같이 행동.

🖥️ PintOS

🔷 Virtual Memory

유튜브 강의

https://www.youtube.com/watch?v=A9WLYbE0p-I

가상 메모리 쓰는 이유

주소 공간 부족
메모리 단편화
보안

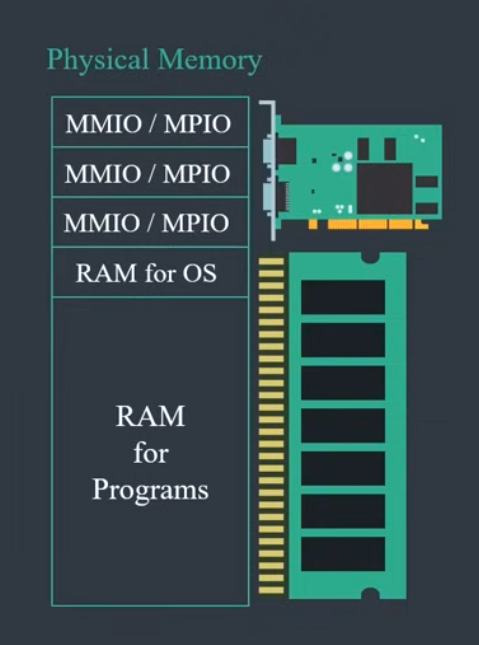
물리 메모리는 입출력 장치, OS, 프로그램을 위해 할당됨

MMIO: 메모리와 장치 간의 입출력을 메모리 공간을 통해 처리하는 방법
MPIO: 스토리지 시스템에서 데이터의 경로를 다중화하는 기술

물리 메모리라고 하면 RAM이라고 알아들으면 된다

램 모자란거 해결법: 공간 없으면 (램에 데이터 없으면, Page Fault 발생하면) 다른 데이터 디스크로 보낸다 (Swap하고)

Swap 계속 일어나는거 : Thrashing

가상 메모리 쓰면 반으로 쪼개서 물리 메모리에 넣을 수 있다. 단편화 해결.

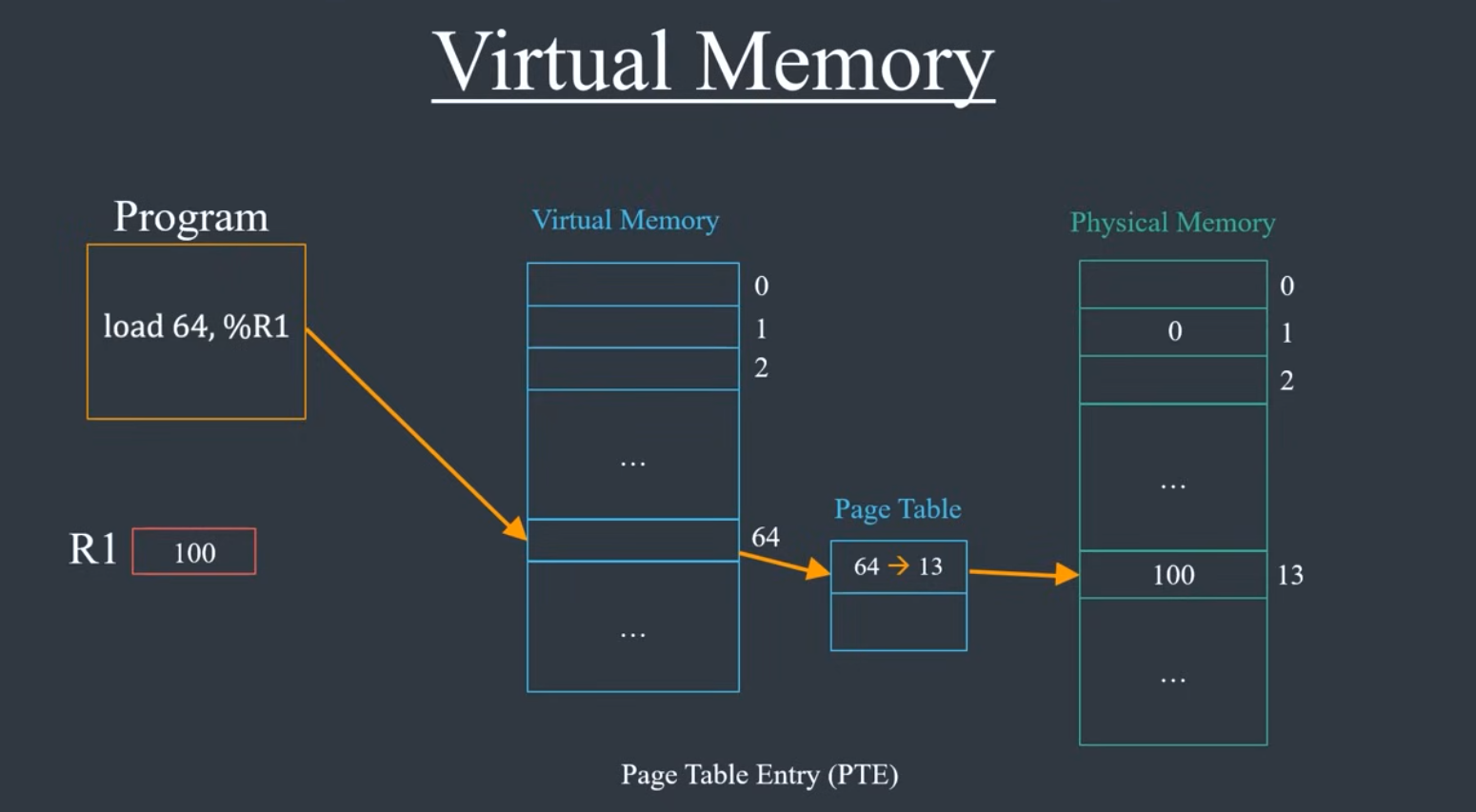
각 프로세스마다 페이지 테이블 있음

가상 메모리를 물리 메모리 주소에 매핑하는거 : 페이지 테이블
각각의 매핑 : 페이지 테이블 엔트리

매핑은 페이지 단위로 한다

페이지에서의 오프셋만큼 페이지에 매핑되는 물리 메모리 시작 주소에서 더한다

https://preamtree.tistory.com/21

요구 페이징과 페이지 폴트

CPU는 물리 메모리를 확인하여 페이지가 없으면 trap을 발생하여 운영체제에 알린다.
운영체제는 CPU의 동작을 잠시 멈춘다.
운영체제는 페이지 테이블을 확인하여 가상 메모리에 페이지가 존재하는지 확인하고, 없으면 프로세스를 중단한다.
페이지 폴트이면, 현재 물리 메모리에 비어있는 프레임(Free Frame)이 있는지 찾는다.
비어있는 프레임에 해당 페이지를 로드하고, 페이지 테이블을 최신화 한다.
중단되었던 CPU를 다시 시작한다.

https://studyandwrite.tistory.com/21

프로세스가 돌아가는 동안 MMU는 실시간으로 페이지 테이블을 확인하고, 필요한 페이지가 물리적 메모리에 있는지를 확인합니다. 이 때 페이지 테이블의 Present bit이 1인지, 0인지 여부가 물리 메모리에 해당 페이지가 저장되어 있는지를 알려줍니다. 또한 페이지 테이블 엔트리에는 해당 페이지가 Swap-out될 때, Backing Storage의 어느 위치에 저장되는지에 대한 정보도 저장하고 있습니다.

한편, 만약 Present bit이 0이면 사용하려는 페이지가 물리적 메모리에 지금 없다는 뜻인데, 우리는 이 상황을 Page Fault라고 합니다.

DMA는 왜 나오는거?

페이지 폴트는 느려서 빨리 해야됨. 그리고 DMA 하면 CPU가 다른 일들 할 때 바로 접근해버릴 수 있음

CPU가 가상 메모리 주소를 물리 메모리 주소로 변환하려고 할 때 TLB(Translation Lookaside Buffer)라는 캐시에 요청함. 이거 개빠름. 사실 MMU(Memory Management Unit)이 함.

TLB도 꽉 차면 Swap같은거 해야됨

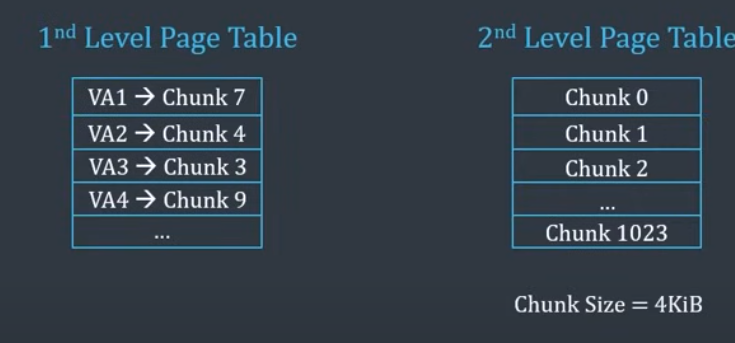
페이지 테이블 여러 레벨로 나눠서 크게 묶기도 함

⚔️ 백준

📌 17940 지하철

# 환승이 최소인 경로들 중에 소요 시간이 가장 짧은 경로를 찾기
# dp 재귀로 풀기. 각 정점에 환승 횟수와 소요 시간을 적기.
# 환승 횟수가 적으면 갱신, 환승 횟수가 같으면 소요 시간을 갱신
import sys
sys.setrecursionlimit(10**6)
def go_next(stn):
    for next, time in enumerate(graph[stn]):
        if time != 0: # 해당 역으로 갈 수 있다면
            # 환승 정보 초기화
            new_trans=dp[stn][0]
            new_time=dp[stn][1]+time
            next_trans = dp[next][0]
            if cpn[stn] != cpn[next]:
                new_trans+=1
            # 환승 횟수가 적거나 같으면 갱신, 아니면 넘어가기
            if new_trans > next_trans:
                continue
            elif new_trans < next_trans:
                dp[next] = [new_trans, new_time]
            else: # 환승 횟수가 같고 시간이 적으면
                if new_time < dp[next][1]:
                    dp[next][1] = new_time
            # 도착한거 아니면 다음으로
            if next != M:
                go_next(next)
                
N,M=map(int,input().split()) # N:지하철역 개수, M: 도착지 번호
cpn=[0]*N # 지하철역 운영 회사 정보 (역은 0부터 N-1까지)
graph=[[] for _ in range(N)]
dp=[[float('inf'),float('inf')] for _ in range(N)]
dp[0]=[0,0]
for i in range(N):
    cpn[i]=int(input())
for i in range(N):
    graph[i]=list(map(int,input().split()))
go_next(0)
print(dp[M][0],dp[M][1]) # 환승 횟수, 소요 시간 출력

new_time 인덱스 실수했었다.

예제는 맞는데 recursion error.
setrecursionlimit(10**7)로 했더니 메모리 초과.

# 환승이 최소인 경로들 중에 소요 시간이 가장 짧은 경로를 찾기
# dp 재귀로 풀기. 각 정점에 환승 횟수와 소요 시간을 적기.
# 환승 횟수가 적으면 갱신, 환승 횟수가 같으면 소요 시간을 갱신
from collections import deque
def bfs(stn):
    Q = deque()
    Q.append(stn)
    while Q:
        stn = Q.popleft()
        for next, time in enumerate(graph[stn]):
            if time != 0: # 해당 역으로 갈 수 있다면
                # 환승 정보 초기화
                new_trans=dp[stn][0]
                new_time=dp[stn][1]+time
                next_trans = dp[next][0]
                if cpn[stn] != cpn[next]:
                    new_trans+=1
                # 환승 횟수가 적거나 같으면 갱신, 아니면 넘어가기
                if new_trans > next_trans:
                    continue
                elif new_trans < next_trans:
                    dp[next] = [new_trans, new_time]
                else: # 환승 횟수가 같고 시간이 적으면
                    if new_time < dp[next][1]:
                        dp[next][1] = new_time
                # 도착한거 아니면 다음으로
                if next != M:
                    Q.append(next)
                
N,M=map(int,input().split()) # N:지하철역 개수, M: 도착지 번호
cpn=[0]*N # 지하철역 운영 회사 정보 (역은 0부터 N-1까지)
graph=[[] for _ in range(N)]
dp=[[float('inf'),float('inf')] for _ in range(N)]
dp[0]=[0,0]
for i in range(N):
    cpn[i]=int(input())
for i in range(N):
    graph[i]=list(map(int,input().split()))
bfs(0)
print(dp[M][0],dp[M][1]) # 환승 횟수, 소요 시간 출력

bfs로 바꿔봤지만 역시 예제만 맞고 메모리 초과.

# 환승이 최소인 경로들 중에 소요 시간이 가장 짧은 경로를 찾기
# dp 재귀로 풀기. 각 정점에 환승 횟수와 소요 시간을 적기.
# 환승 횟수가 적으면 갱신, 환승 횟수가 같으면 소요 시간을 갱신
def dfs(stn):
    stack = []
    stack.append(stn)
    while stack:
        stn = stack.pop()
        for next, time in enumerate(graph[stn]):
            if time != 0: # 해당 역으로 갈 수 있다면
                # 환승 정보 초기화
                new_trans=dp[stn][0]
                new_time=dp[stn][1]+time
                next_trans = dp[next][0]
                if cpn[stn] != cpn[next]:
                    new_trans+=1
                # 환승 횟수가 적거나 같으면 갱신, 아니면 넘어가기
                if new_trans > next_trans:
                    continue
                elif new_trans < next_trans:
                    dp[next] = [new_trans, new_time]
                else: # 환승 횟수가 같고 시간이 적으면
                    if new_time < dp[next][1]:
                        dp[next][1] = new_time
                # 도착한거 아니면 다음으로
                if next != M:
                    stack.append(next)
                
N,M=map(int,input().split()) # N:지하철역 개수, M: 도착지 번호
cpn=[0]*N # 지하철역 운영 회사 정보 (역은 0부터 N-1까지)
graph=[[] for _ in range(N)]
dp=[[float('inf'),float('inf')] for _ in range(N)]
dp[0]=[0,0]
for i in range(N):
    cpn[i]=int(input())
for i in range(N):
    graph[i]=list(map(int,input().split()))
dfs(0)
print(dp[M][0],dp[M][1]) # 환승 횟수, 소요 시간 출력

큐 메모리 때문인가 해서 dfs로 바꿔봤지만 역시 메모리 초과.
테이블 선언에 뭔가 문제가 있을리는 없음.

경로 탐색할 때 최적화를 해줘야 할듯.

# 도착지 환승 횟수보다 크면 넘어가기
if new_trans > dp[M][0]:
    continue

환승 횟수 확인하고 불필요한 경우 최적화하는 로직 추가해줬더니
이젠 메모리 초과 대신 시간 초과 뜸.
(이거 원래 더 빨리 떠올렸었는데 풀다가 까먹었다.
효율에 critical한 거면 적어놓을 것.)

0인것들 매번 훑지 않게 연결된 인덱스를 저장해줘야할듯.

for i in range(N):
    temp=list(map(int,input().split()))
    for stn, time in enumerate(temp):
        if time != 0:
            graph[i].append((stn,time))

저장해도 시간 초과.

경로 탐색 로직 자체를 다시 생각해보자.

환승 횟수가 갱신돼었을 때 다시 경로를 다 따라가면서 환승 횟수를 갱신해주는게 문제.
bfs로 다시 바꿔보는게?

바꿔도 시간 초과.

흑흑흑 있을 때 환승 횟수가 그대로니까 계속 큐에 들어가는게 문제인듯.
재귀 dp에 visited 넣고 역탐색하면 될듯?

역탐색 이유 : visited가 유효하게 작용하려면 역탐색해야됨

import sys
sys.setrecursionlimit(10**5)
def min_trans(stn):
    visited[stn]=True
    for pre, time in graph[stn]:
        if not visited[pre]:
            new_trans = min_trans(pre)
            new_time = dp[pre][1]+time
            if cpn[stn] != cpn[pre]:
                new_trans += 1
            if new_trans > dp[stn][0]:
                continue
            elif (new_trans < dp[stn][0]) or (dp[stn][1] > new_time):
                dp[stn] = [new_trans,new_time]
    return dp[stn][0]

흑흑흑을 다시 안 돌아오게 하려고 visited 체크했는데 시간 초과는 해결됐지만 틀렸습니다 뜸.
이렇게 되면 교차하는 경로 있을 때 제대로 체크 못할듯

아니 애초에 그냥
그래프가 양방향 그래프라서 갔다가 돌아오는거 자체가 문제였음

정방향 dfs한 다음에 환승 횟수 기준으로 경로 중단하면 안 돌아오지 않을까?

그게 아까 처음에 했던 생각이었다...
graph 최적화는 새롭게 시킨거니까 메모리 초과 대신 시간 초과가 뜨긴 했는데
결국 정점 중복에 관한 문제를 풀어야 됨.

일단 dfs 했던 코드로 해보기.

# 환승 횟수가 적거나 같으면 갱신, 아니면 넘어가기
if new_trans > next_trans:
    continue
elif new_trans < next_trans:
    dp[next] = [new_trans, new_time]
else: # 환승 횟수가 같고 시간이 적으면
    if new_time < dp[next][1]:
        dp[next][1] = new_time
    else:
        continue

else continue 추가하면 될 줄 알았는데 시간초과.
흑흑흑일때 시간이 더해지니까 그때는 스택에 추가 안하는 식으로 하면 되야 하는 거 아닌가 왜 안되지

from collections import deque
def bfs(stn):
    Q = deque()
    Q.append(stn)
    while Q:
        stn = Q.popleft()
        for next, time in graph[stn]:
            # 환승 정보 초기화
            new_trans=dp[stn][0]
            new_time=dp[stn][1]+time
            next_trans = dp[next][0]
            if cpn[stn] != cpn[next]:
                new_trans+=1
            # 환승 횟수가 적거나 같으면 갱신, 아니면 넘어가기
            if new_trans > next_trans or new_trans > dp[M][0]:
                continue
            elif new_trans < next_trans:
                dp[next] = [new_trans, new_time]
            else: # 환승 횟수가 같고 시간이 적으면
                if new_time < dp[next][1]:
                    dp[next][1] = new_time
                else:
                    continue
            # 도착한거 아니면 다음으로
            if next != M:
                Q.append(next)
            
N,M=map(int,input().split()) # N:지하철역 개수, M: 도착지 번호
cpn=[0]*N # 지하철역 운영 회사 정보 (역은 0부터 N-1까지)
graph=[[] for _ in range(N)]
dp=[[float('inf'),float('inf')] for _ in range(N)]
dp[0]=[0,0]
for i in range(N):
    cpn[i]=int(input())
for i in range(N):
    temp=list(map(int,input().split()))
    for stn, time in enumerate(temp):
        if time != 0:
            graph[i].append((stn,time))
bfs(0)
print(dp[M][0],dp[M][1]) # 환승 횟수, 소요 시간 출력