https://swexpertacademy.com/main/code/problem/problemDetail.do?problemLevel=3&contestProbId=AYcllbDqUVgDFASR&categoryId=AYcllbDqUVgDFASR&categoryType=CODE&problemTitle=&orderBy=FIRST_REG_DATETIME&selectCodeLang=ALL&select-1=3&pageSize=10&pageIndex=1

문제 개요

정수 N이 주어질 때, 원점을 중심으로 반지름이 N인 원 안에 포함되는 격자점(x, y좌표가 모두 정수인 점)의 개수를 구하세요.

문제 접근

원점을 기준으로 원을 그렸을 때 작은 순서대로 계산해봅시다.
N=1일때, 5 (1 + 4)
N=2일때, 13 (1 + 4) + (4 + 4)
N=3일때, 29 (1 + 4) + (4 + 4) + (12 + 4)
N=4일때, 49 (1 + 4) + (4 + 4) + (12 + 4) + (16 + 4)
N=5일때, 81 (1 + 4) + (4 + 4) + (12 + 4) + (16 + 4) + (20 + 12)
패턴을 못 찾겠습니다.

다른 방법으로 접근해 봅시다.
$(x,y)\in\{(x,y): x^2+y^2\leq N^2|x,y\in\N\}$인 (x,y)의 개수를 찾아야 합니다.
x가 N일때부터 1일때까지 내려가면서 둘의 합이 N의 제곱보다 낮으면 카운트하는 것을 반복합니다. 그렇게 되면 한 사분면에서 가질 수 있는 격자점의 개수를 가지게 됩니다.

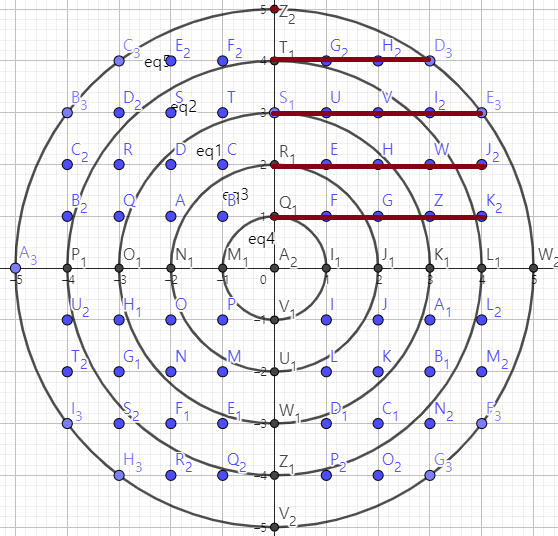
빨간 선으로 나타낸 것이 한 사분면의 격좌점들 입니다. 이것이 총 4개 존재하므로 4곱하면 원점을 제외한 격좌점의 개수를 얻을 수 있습니다.

N이 200 이하기 때문에, 브루트 포스 방법으로도 풀 수 있을 것 같습니다.

import java.util.Scanner;

public class Solution {
    static void solve(int number){
        int count = 0;
        for(int i=number;i>0;i--){
            for(int j=0;j<number;j++){
                if(j*j + i*i > number*number){
                    break;
                }
                count++;
            }
        }
        System.out.println(String.format("#%d %d", number, count*4 + 1));
    }

    public static void main(String args[]) throws Exception{
        Scanner sc = new Scanner(System.in);
        int T;
        int n;
        T=sc.nextInt();

        for(int test_case = 1; test_case <= T; test_case++){
            n = sc.nextInt();
            solve(n);
        }
    }
}