[C++]백준 11660 : 구간 합 구하기 5

누적합(Prefix Sum)

배열의 각 위치까지의 누적합을 저장한 배열이다.
이를 통해 배열의 일부 구간의 합을 보다 빠르게 계산할 수 있다.

• 배열에 값을 저장하고 지정된 인덱스부터 하나씩 더해가는 방식은 최악의 경우 O(n2)의 시간복잡도를 갖기 때문에 범위가 클 때 사용X
• Prefix sum 방식을 사용하면 O(N)으로 해결할 수 있다.

1차원 누적합

index	1	2	3	4	5
배열(An)	3	4	10	2	9
누적합(Sn)	3	7	17	19	28

만약 그냥 배열로 1~4까지 구간 합을 구한다면 4 + 10 + 2 + 9 = 25
하지만, 누적합을 사용하면 S4 - S0 = 25

작은 범위라 별 차이 없어보이지만 수가 커지면 누적합이 효율적이다!

2차원 누적합

2차원 누적합은 A00 ~ Aij까지의 합이다.

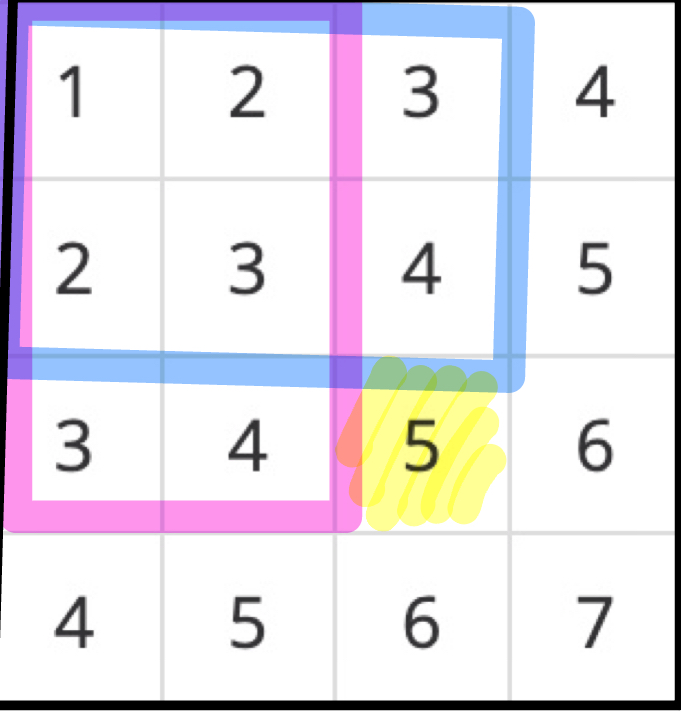
위의 그림에서 (3,3)의 누적합을 구하고 싶으면 파란 구간과 분홍 구간을 더한 후 겹치는 부분을 빼고 해당 배열의 값을 더해주면 된다.
식으로 나타내보면
prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + arr[i][j] 로 나타낼 수 있다.

백준 11660번

문제 링크 : https://www.acmicpc.net/problem/11660

생각의 흐름
처음에 봤을 때 행 마다 누적합을 구하여서 x1행부터 x2행까지 (y1~y2)의 구간합을 다 더해서 풀자고 생각했다.

#include <iostream>

using namespace std;

int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    int N,M;
    cin>>N>>M;
    int Psum[N+1][N+1];
    for(int i=0;i<=N;i++){
        for(int j=0;j<=N;j++){
            if(i==0 || j==0) Psum[i][j] = 0;
            else{
                int num;
                cin>>num;
                Psum[i][j] = Psum[i][j-1] + num;
            }
        }
    }
    while(M--){
        int sum = 0;
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        for(int i=x1;i<=x2;i++){
            sum += Psum[i][y2] - Psum[i][y1-1];
        }
        cout<<sum<<'\n';
    }
}

누적 합을 공부하면서 이렇게 풀면 이보다 더 큰 수가 나왔을때는 통과하지 못 할 수도 있다는 것을 알았다.
그래서 두 번째 풀이는 2차원 배열의 모든 누적합을 구한 후 푸는 것이었다.

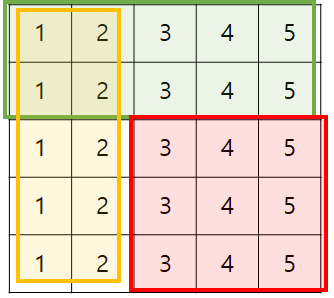
여기서 내가 (3,3)~(5,5)까지의 구간 합을 구하고 싶다면
prefix[5][5]-prefix[2][5]-prefix[5][2]+prefix[2][2]
로 구할 수 있다.
따라서 (x1,y1)~(x2,y2)의 구간 합을 구하려면
prefix[x2][y2]-prefix[x1-1][y2]-prefix[x2][y1-1] + prefix[x1-1][y1-1]
이렇게 한 번에 구할 수 있다.

#include <iostream>

using namespace std;

int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    int N,M;
    cin>>N>>M;
    int prefix[N+1][N+1];
    for(int i=0;i<=N;i++){
        for(int j=0;j<=N;j++){
            if(i==0 || j==0)prefix[i][j] = 0;
            else{
                int a;
                cin>>a;
                prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + a;
            }
        }
    }
    
    while(M--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<prefix[x2][y2] - prefix[x1-1][y2] - prefix[x2][y1-1] + prefix[x1-1][y1-1]<<'\n';
    }
}

확실히 시간이 줄어들었다.