그리디 알고리즘

그리디 알고리즘은 현재 상황에서 지금 당장 좋은 것만 고르는 방법으로 탐욕적으로 푸는 알고리즘 이다.

한 마디로 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 의미한다. 그리디 알고리즘은 매 순간 가장 좋아보이는 것을 선택하며, 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않는다.

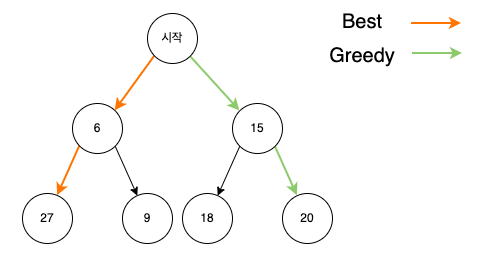
위와 같은 트리에서 시작점에서 시작해서 가장 큰 값을 구해야 한다고 가정했을 때 가장 큰 값을 구하는 경로는 시작 -> 6 -> 27로 가장 큰 값을 27인데 그리디 알고리즘으로 구하면 현재 상황에서 가장 큰 값을 선택하기 때문에 시작 -> 15 -> 20을 선택한다.

크루스칼 알고리즘

신장 트리 중에서 최소 비용으로 만들 수 있는 신장 트리를 찾는 알고리즘을 '최소 신장 트리 알고리즘'이라고 하는데 그 중 대표적인 알고리즘으로는 크루스칼 알고리즘이 있다.

• 신장트리: 그래프에서 모든 노드가 사이클 없이 연결된 부분
  

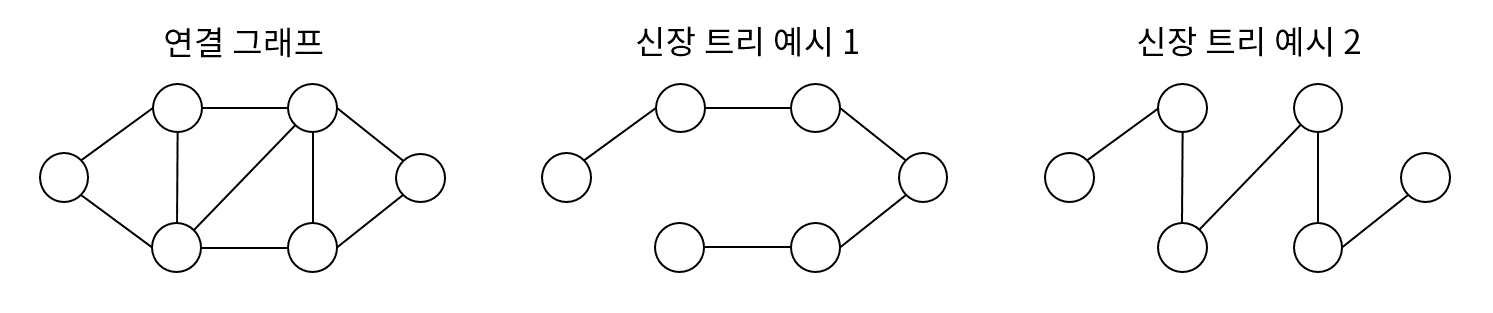
크루스칼 알고리즘 동작 과정
1. 간선 데이터를 가중치에 따라 오름차순으로 정렬
2. 하나씩 확인하며 사이클을 발생시키는지 확인(노드의 부모가 같은지 확인)

• 사이클이 발생하지 않는 경우 최소 신장 트리에 포함
• 사이클이 발생하는 경우 최소 신장 트리에 포함 X

3. 모든 간선에 대해서 2번 과정 반복

섬 연결하기

문제를 30분 동안 봤는데 진짜 어떤식으로 풀어야할 지 잘 모르겠어서 찾아봤다. 크루스칼 알고리즘으로 풀면 된다고 봐서 했다. 크루스칼 알고리즘을 알고리즘 수업때 보고 한 번도 풀어본 적이 없어서 다시 공부했다.
푸는데 계속 문제가 꼬이고 어렵게 생각해서 잘 안풀렸다. 그리고 부모 노드를 확인할때 getParent함수를 안쓰고 그냥 배열에 부모노드 번호를 저장해놓고 풀어서 안 풀렸다.

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>

using namespace std;

int parent[101];

//부모 노드 찾는 함수
int getParent(int node){
  if(node == parent[node]) return node;
  else{
    return parent[node] = getParent(parent[node]);
  }
}

//비교 함수
bool cmp(vector<int> a, vector<int> b){
  return a[2] < b[2];
  }

int solution(int n, vector<vector<int>> costs){
  int answer = 0;

  //부모노드 저장하는 배열 초기화
  for(int i=0;i<n;i++){
    parent[i] = i;
  }
  //costs를 거리 기준으로 오름차순 정렬
  sort(costs.begin(),costs.end(),cmp);
 
  for(int i=0;i<costs.size();i++){
    int a = getParent(costs[i][0]);
    int b = getParent(costs[i][1]);
    int c = costs[i][2];
    if(a!=b){
      answer += c;
      parent[b] = a;
    }
  }

  return answer;
}

int main(void){
  int n = 4;
  vector<vector<int>>costs = {{0,1,1},{0,2,2},{1,2,5},{1,3,1},{2,3,8}};
  cout<<solution(n,costs)<<'\n';
}

어려웠다..