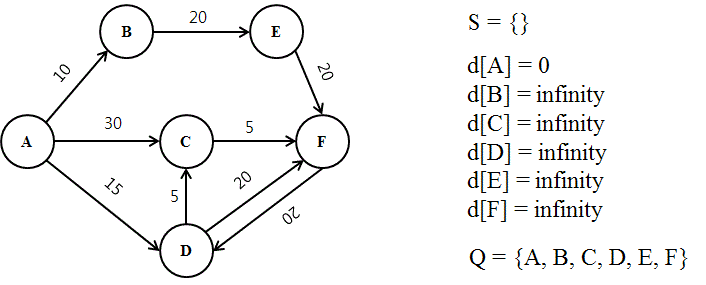
다익스트라 알고리즘

다익스트라 알고리즘은 그래프에서 한 정점에서 모든 다른 정점까지의 최단 경로를 구하는 알고리즘 입니다.

동작 과정
1. 출발 노드와 도착 노드를 설정하여 최단 거리 테이블을 초기화 한다.


2. 현재 위치한 노드의 인접 노드 중에서 방문하지 않은 노드들 중 거리가 가장 짧은 노드를 선택한다.

3. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신

• 현재 테이블의 최단거리보다, 해당 노드를 거쳐가는 비용이 작으면 작은 경로로 교체

4. 2번과 3번을 반복한다.

풀이

Dij함수를 만들어서 s, a, b의 최단거리들을 구하고
if (answer > dists[i] + dista[i] + distb[i]) { answer = dists[i] + dista[i] + distb[i]; }
이런 식으로 제일 최소 비용이 나오는 i 값을 찾아주었다.

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <queue>

using namespace std;

const int INF = 100000000;

vector<int> Dij(int k, int n, vector<vector<int>>& d, vector<vector<int>>& v) {
    vector<bool> visited(n + 1, false);
    vector<int> dist(n + 1, INF);
    dist[k] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
    pq.push({0, k});

    while (!pq.empty()) {
        int currentDist = pq.top().first;
        int num = pq.top().second;
        pq.pop();

        if (visited[num]) continue;
        visited[num] = true;

        for (int i = 0; i < v[num].size(); i++) {
            int next = v[num][i];
            int nextDist = currentDist + d[num][next];

            if (dist[next] > nextDist) {
                dist[next] = nextDist;
                pq.push({nextDist, next});
            }
        }
    }

    return dist;
}

int solution(int n, int s, int a, int b, vector<vector<int>> fares) {
    vector<vector<int>> d(n + 1, vector<int>(n + 1, INF));
    vector<vector<int>> adj(n + 1);
    for (int i = 1; i <= n; i++) {
        d[i][i] = 0;
    }

    for (int i = 0; i < fares.size(); i++) {
        int u = fares[i][0];
        int v = fares[i][1];
        int cost = fares[i][2];
        d[u][v] = cost;
        d[v][u] = cost;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    vector<int> dists = Dij(s, n, d, adj);
    vector<int> dista = Dij(a, n, d, adj);
    vector<int> distb = Dij(b, n, d, adj);

    int answer = INF;

    for (int i = 1; i <= n; i++) {
        if (answer > dists[i] + dista[i] + distb[i]) {
            answer = dists[i] + dista[i] + distb[i];
        }
    }

    return answer;
}

다익스트라를 오랜만에 공부해보고 우선순위 큐도 잘 몰라서 푸는데 어려웠던 것 같다.
다익스트라랑 우선순위 큐는 다시 공부해봐야겠다..

플로이드 워셜

플로이드 워셜 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구하는 알고리즘이다. 거쳐가는 중간 노드를 기준으로 최단 거리를 구한다.

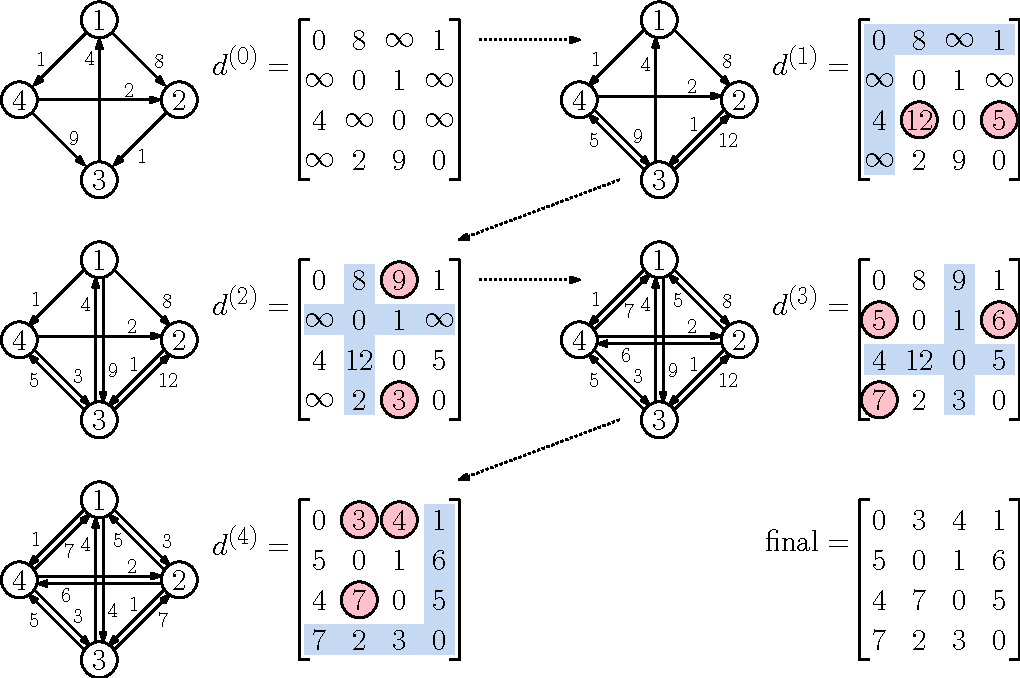
이렇게 1번노드를 거칠때, 2번 노드를 거칠때를 계속 방문하면서 배열을 갱신해준다.

플로이드 워셜 알고리즘의 점화식
Dab = min (Dab,Dak + Dkb

풀이

거리 배열을 초기화 시켜주고 반복문으로 한 노드씩 돌면서 계산해주었다.

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

const int INF = 100000000;

int solution(int n, int s, int a, int b, vector<vector<int>> fares){
  vector<vector<int>> d(n+1,vector<int>(n+1, INF));

  for(int i=1;i<=n;i++){
    d[i][i] = 0;
  }

  for(int i=0;i<fares.size();i++){
      int a = fares[i][0];
      int b = fares[i][1];
      int c = fares[i][2];
      d[a][b] = c;
      d[b][a] = c;
  }

  for(int k=1;k<=n;k++){
    for(int i=1;i<d.size();i++){
      for(int j=1;j<d[i].size();j++){
        if(d[i][j] > d[i][k] + d[k][j]){
          d[i][j] = d[i][k] + d[k][j];
        }
      }
    }
  }

  int answer = INF;

  for(int i=1;i<=n;i++){
    if(answer > d[s][i] + d[i][a] + d[i][b]){
      answer = d[s][i] + d[i][a] + d[i][b];
    }
  }
  
  return answer;
}

int main(void){
  int n= 6, s= 4, a = 6, b = 2;
  vector<vector<int>> fares = {{4,1,10},{3,5,24},{5,6,2},{3,1,41},{5,1,24},{4,6,50},{2,4,66},{2,3,22},{1,6,25}};
  int result =  solution(n,s,a,b,fares);
  cout<<result<<'\n';
  
}

플로이드 워셜 방법으로는 잘 풀어냈다!