경로 탐색

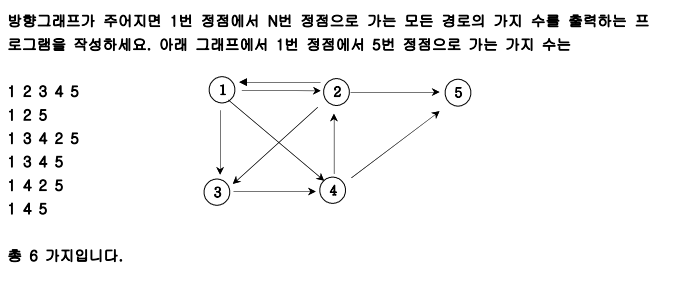
문제

제한 사항

입출력 예

풀이

function solution(n, arr) {
  let answer = 0;
  let check = Array.from({ length: n + 1 }, () => 0); // check용, n+1개인 이유는 노드를 1번부터 할거기때문 0번노드(인덱스는) 없는 취급하자.
  let graph = Array.from(Array(n + 1), () => Array(n + 1).fill(0));

  for (let [a, b] of arr) {
    graph[a][b] = 1; // 방향그래프
    // graph[b][a] = 1; // 이렇게 둘다 해주면 무방향 그래프
  }
  // 인접행렬.
  function DFS(v) {
    if (v === n) {
      // 마지막 노드에 도착하면.
      answer++;
    } else {
      for (let i = 1; i <= n; i++) {
        //정점 번호
        if (graph[v][i] === 1 && check[i] === 0) {
          check[i] = 1;
          DFS(i);
          check[i] = 0;
        }
      }
    }
  }
  check[1] = 1; // 1번노드 미리 체크하고 출발해야함. (출발점이니까 처음에 들르고 다신 안들름.)
  DFS(1);
  return answer;
}

let arr = [
  [1, 2],
  [1, 3],
  [1, 4],
  [2, 1],
  [2, 3],
  [2, 5],
  [3, 4],
  [4, 2],
  [4, 5],
]; // 간선 정보 => 인접행렬을 만들 때 필요한 재료
console.log(solution(5, arr));

• 간선 정보를 그래프로 만드는 방법이 두가지 있다 위 코드는 인접행렬을 이용해서 나태냈다.

function solution2(n, arr) {
  let answer = 0;
  let check = new Array(n + 1).fill(0);
  let graph = {};
  for (let i = 1; i <= n; i++) {
    graph[i] = [];
  }

  for (let [a, b] of arr) {
    graph[a].push(b);
  }

  function dfs(v) {
    if (v === n) {
      answer++;
    } else {
      for (let i = 0; i < graph[v].length; i++) {
        let next = graph[v][i];
        if (!check[next]) {
          check[next] = 1;
          dfs(next);
          check[next] = 0;
        }
      }
    }
  }
  check[1] = 1;
  dfs(1);

  return answer;
}

console.log(solution2(5, arr));

• 인접 리스트를 활용한 방법이다.
• 노드가 늘어날수록 인접 리스트가 효율적이다.