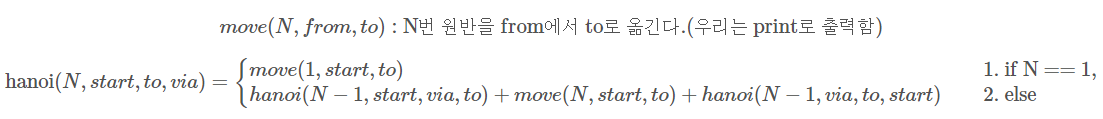하노이 탑 알고리즘

게임 설명

이미지 출처

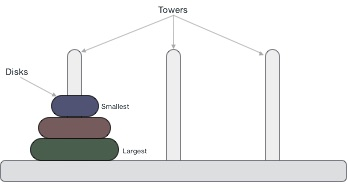
• 간단히 설명하면 원반(disk) 옮기기 퍼즐이다.
• 하노이의 탑에는 서로 크기가 다른 원반이 n개 있고 원반을 끼울 수 있는 기둥이 세 개 있다. 어떻게 하면 원반 n개를 맨 왼쪽 기둥에서 맨 오른쪽 기둥으로 모두 옮길 수 있을까를 고민해보는 문제다.
• 하노이의 탑 규칙을 정리하면 아래와 같다.

세부 규칙

• 크기가 다른 원반 n개를 시작 기둥에서 도착 기둥으로 모두 옮겨야 한다.
• 원반은 한 번에 한 개씩만 옮길 수 있다.
• 원반을 뽑을 땐 기둥의 맨 위의 원반을 뽑아야 한다. (중간에 있는 원반은 어떤 경우에도 뽑을 수 없다.)
• 원반을 쌓을 땐 기둥의 맨 위에 쌓아야 한다. (원반과 원반 사이에 끼워 넣을 수 없다.)
• 원반을 쌓을 땐 큰 원반 위에 작은 원반을 올려야 한다. (작은 원반 위에 큰 원반을 올릴 수 없다.)

풀이

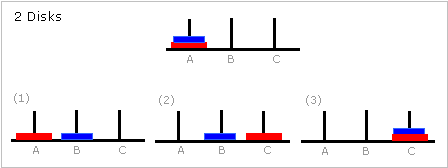
원반이 2개일 때

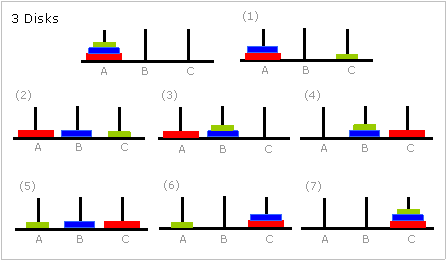
총 3번 이동
1번 원반을 1에서 2로 이동
2번 원반을 1에서 3로 이동
1번 원반을 2에서 3로 이동

원반이 3개일 때

총 7번 이동
1번 원반을 1에서 3로 이동
2번 원반을 1에서 2로 이동
1번 원반을 3에서 2로 이동
3번 원반을 1에서 3로 이동
1번 원반을 2에서 1로 이동
2번 원반을 2에서 3로 이동
1번 원반을 1에서 3로 이동

이미지 출처

• 원반이 한 개라면, 시작 기둥에서 도착 기둥까지 1회만에 옮길 수 있다.
• 원반이 두 개 이상이면 원반의 개수를 n 이라 할 때,
  1. 가장 아래에 있는 원반 n을 도착 기둥에 옮기기 위해 그 위에 놓여 있는 n-1개의 원반을 보조 기둥에 옮긴다.
  2. 원반 n을 도착 기둥에 옮긴다.
  3. 보조 기둥에 있는 n-1개의 원반을 도착 기둥에 옮긴다.
• 재귀적인 방법을 사용해 문제를 해결할 수 있다.
• 파이썬 재귀 함수로 구현하면 아래와 같다.

파이썬 코드 구현 및 실행

MOVE_MESSAGE = "{}번 원반을 {}에서 {}로 이동"


def move(N, start, destination):
    print(MOVE_MESSAGE.format(N, start, destination))


def hanoi(n, start, destination, via):
    """
    하노이의 탑 규칙에 따라 원반을 옮기고,
    옮길 때마다 원반의 시작 위치와 이동한 위치를 출력합니다.
    마지막으로 총 이동 횟수를 반환합니다.
    :params
        n: 총 원반 개수
        start: 시작 기둥
        destination: 도착 기둥
        via: 보조 기둥:
    :return count:
    """
    # 원반이 1개일 때 시작 기둥에서 도착 기둥까지 한 번에 이동
    if n <= 1:
        move(1, start, destination)
        return 1

    count = 0
    # 원반 n-1개를 시작 기둥에서 보조 기둥으로 이동
    count += hanoi(n - 1, start, via, destination)

    # 가장 큰 원반을 시작 기둥에서 도착 기둥으로 이동
    count += 1
    move(n, start, destination)

    # 원반 n-1개를 보조 기둥에서 도착 기둥으로 이동
    count += hanoi(n - 1, via, destination, start)

    return count


if __name__ == '__main__':
    n = 3
    start = 1
    destination = 3
    via = 2

    total_count = hanoi(n, start, destination, via)
    print('총 이동 횟수:', total_count)


'''
출력 결과

1번 원반을 1에서 3로 이동
2번 원반을 1에서 2로 이동
1번 원반을 3에서 2로 이동
3번 원반을 1에서 3로 이동
1번 원반을 2에서 1로 이동
2번 원반을 2에서 3로 이동
1번 원반을 1에서 3로 이동
총 이동 횟수: 7
'''

점화식

• 위의 풀이는 아래 식으로 정리할 수 있다.

수식 출처

• 또한, 풀이를 토대로 아래와 같이 점화식을 세울 수 있다.

먼저 " 수열 ${a_n}$= ${n}$개의 원판을 이동하는 횟수 " 라고 정의하자.
${n}$개의 원판을 이동시키기 위해서는 그 위의 ${n}$-${1}$개의 원판을 다른 막대로 이동하고 맨 아래쪽 원판을 도착지로 이동해야 한다. 그리고 다시 ${n}$-${1}$개의 원판을 이동해야 하므로 다음과 같은 점화식이 성립한다.
=>   ${a_n}$ = 2${a_{n-1}}$ ${+}$ ${1}$
그리고 이를 일반항으로 풀어내면 ${{2^n} - 1}$ 임을 알 수 있다.
참고

시간 복잡도

• 위의 점화식을 생각했을 때 결국 n개의 원반을 모두 옮기기 위해서는
  ${{2^n} - 1}$ 번의 이동이 필요하고,
• 시간 복잡도는 O(${2^n}$) 으로 볼 수 있다.

관련 문제

• 백준 - 1914번 하노이 탑

Ref

• 모두의 알고리즘 with 파이썬 - 이승찬님
• '하노이의 탑' 이해하기 - Parkito's on the way!