겹치지 않게 순서를 결정하는 대표 유형이다. 흔히 힙(Heap) 알고리즘을 이용하여 해결한다. 이 문제를 정리해 두면 Heap 알고리즘을 이해하는 데 한결 도움이될 것 같아 소개해 본다.
먼저 Softeer에 강의실 배정 문제이다. [ 문제 보기 ]
문제 설명
겹치지 않게 강의 시간표를 짜는 문제이다. 즉, 주어진 입력 중에 시간이 겹치지 않게 선택해서 최대한 많은 수의 강의를 담는다.
풀이
입력은 시작 시간과 끝나는 시간이 주어지고, 우리는 제일 빨리 끝나는 수업을 먼저 담아야 한정된 시간 안에 최대한 많은 강의를 담을 수 있다는 것을 안다. 여기서 Heap 알고리즘을 이용한다. ➡ 끝나는 시간을 기준으로 Heap 정렬을 한다.
강의를 담기 전에는 현재 시간이 강의의 시작 전 인지를 확인하고 담는다. 강의를 담은 후에는 끝나는 시간을 현재시간으로 세팅해 주면 반복했을 때 겹치지 않게 된다.
아래는 정답 코드이다.
import heapq
n = int(input())
arr = []
for _ in range(n):
a, b = map(int,input().split())
heapq.heappush(arr,(b,a)) # 끝나는 시간을 기준으로 할 것이기에 (b,a)
ans = 0
now = 0
while arr:
#가장 빨리 끝나는 수업을 뽑고 다시 힙 정렬
b,a = heapq.heappop(arr)
# 아직 시작 시간을 지나지 않았다면
if a >= now:
ans += 1 # 담는다.
now = b # 현재 시간을 끝나는 시간으로 맞춰준다.
print(ans)한번 생각해 본 것
for _ in range(n):
a, b = map(int,input().split())
# 먼저 배열에 넣음
arr.append((b,a)) # 끝나는 시간을 기준으로 할 것이기에 (b,a)
# arr을 힙 변환
heapq.heapify(arr)여기서 내가 고려했던 건, arr에 append로 입력을 받고 heapify로 한꺼번에 힙 변환해 주면 더 빠르지 않을까 하는 생각이었다.
때문에 heappush와 append➡heapify , 이 둘은 어떤 차이가 있는지 알아봤다.
단순 n개를 append를 하는 것은 시간복잡도가 O(n)이고 heapify 또한 O(n)인 반면, heappush는 n번 시행하면 O(nlogn)이기 때문에 heapify를 사용하는 게 더 좋지 않을까 생각해 봤다. 
실제로 위처럼 작성해서 시간을 측정해 보았다. 첫 번째는 heappush를 이용했고 두 번째는 append를 이용하여 arr에 담고 한꺼번에 heapify를 진행한다. 실제 수행시간은 엎치락뒤치락 큰 차이가 없었다. 시간복잡도가 실제 수행시간은 아니니깐 말이다. 그러나 정말 커진다면 차이가 있지 않을까 예상해 본다.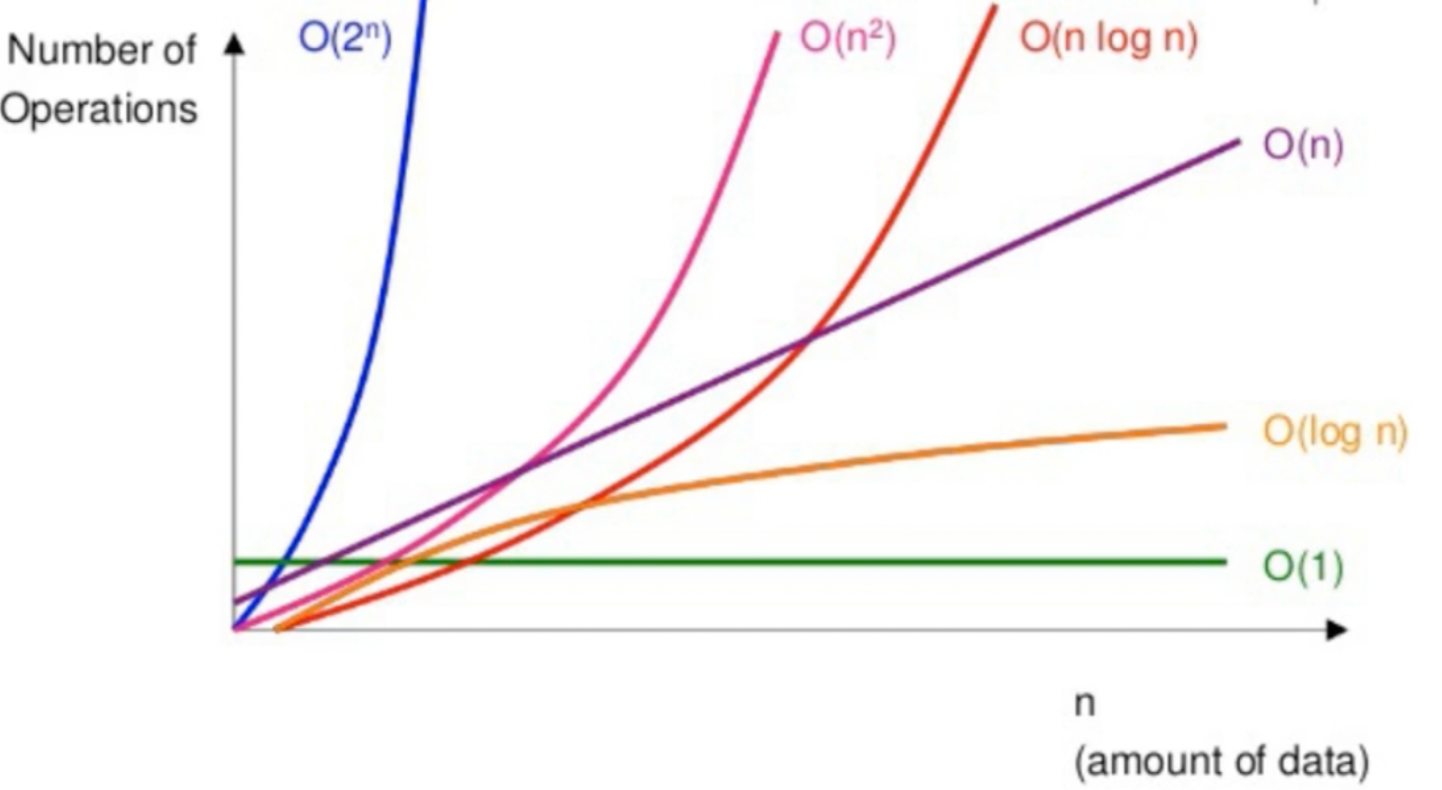
이번엔 프로그래머스에 디스크 컨트롤러 문제이다.[ 문제 보기 ]
2번 문제 설명
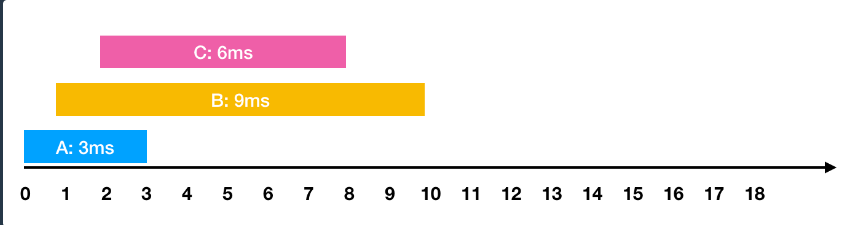이는 입력으로 작업의 요청 시점과 작업 소요 시간이 들어온다.
들어온 요청을 모두 수행할 때 대기했던 시간을 최소화하는 문제이다.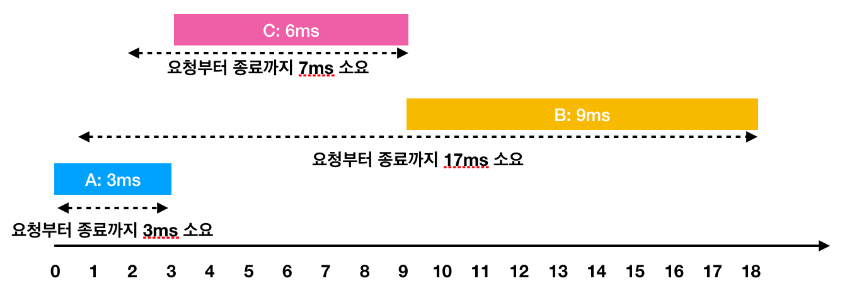
모든 것을 겹치지 않고 전부 처리해야 하므로 A➡B➡C 순으로 처리를 해도 최종 종료시간은 모두 같지만, 위에처럼 A➡C➡B 순으로 해결하면 요청부터 종료까지의 대기시간 총합의 평균이 가장 적은 것을 알 수 있다.
풀이
이 문제도 heap 알고리즘의 흔한 유형으로 강의실 배정 문제와 차이는
입력이 시작과 끝이 아닌, 요청 시점과 처리시간으로 들어온다는 것이 다르고
다음으로 처리할 요청이 C일지 B일지 선택하는 기준은 현재를 기준으로 가장 빠르게 처리할 수 있는 것을 선택해야 한다는 점이다.
따라서 현재를 기준으로 처리 가능한 작업들을 모두 heap에 넣고 가장 빠르게 끝나는 것을 뽑아서 처리하면 된다.
나머지는 모두 첫 번째 문제와 유사하다.
import heapq
def solution(jobs):
n = len(jobs)
answer,cnt,now = 0, 0, 0 #cnt는 처리한 작업의 수
heap = []
start = -1 # 가장 최근에 시작된 작업의 시작 시간
# 모두 처리하면 끝
while cnt != n:
# 현재 처리할 수 있는 작업인지 모두 확인
for job in jobs:
# 요청 시간이 되었거나 현재보다 더 지났다면 처리 가능
if start < job[0] <= now:
# 처리하는 데 걸리는 시간을 기준으로 담음
heapq.heappush(heap,[job[1],job[0]])
# heap에 처리할 게 있다면
if len(heap) != 0:
# 가장 빠르게 처리할 수 있는 것을 pop
[b,a] = heapq.heappop(heap)
#작업 시작이 지금이 됨
start=now
now += b
# 대기시간 = 현재 - 요청 시간
answer += now - a
# 작업 완료
cnt += 1
else:
#작업할게 없다면 시간을 1 넘김
now += 1
return answer // n회고
지난 시간에는 heap의 개념과 정렬 과정을 학습했다. 그러나 아직 heap 함수를 사용하는 부분에서 어색함을 느꼈다. 이번 시간에는 heap을 활용한 대표적인 유형에 대해 더 자세히 학습했는데, 현재를 기준으로 처리가 가능한지 확인하고, 현재 시간을 업데이트하는 방법 등 전체적인 틀은 비슷한 것 같다. heap 자료구조를 사용할 때 중요한 것은 무엇을 push하고 pop 하는지, 그리고 그 기준을 결정하는 것이 관건인 듯하다.
1번 문제에서는 두 가지 방식을 고려해 보았는데, 2번 문제에서는 heapify를 사용하는 것이 적절하지 않았다는 것을 깨달았다. 그 이유는 한 번에 담아서 정렬하는 것이 아닌, 상황에 맞게 매번 담아야 했기 때문이다. 여전히 부족한 부분이 많지만, 어떻게 문제에 접근해야 하는지를 고민하는 시간이 되었다.
