heap 알고리즘 문제 회고

프로그래머스 - 더 맵게 라는 문제를 풀면서 의문점이 생겼다.. 대표적으로 알려진 알고리즘 해법이 아래처럼 heap을 사용한다.

설명

아래는 대표적으로 알려진 heap풀이이다.
문제를 간략 요약하자면 ➡ 가장 낮은 숫자와 두 번째로 낮은 숫자 섞는다. ➡ K보다 큰지 비교한다.➡ K보다 커졌을 때 몇 번 섞었는지를 출력한다.

import heapq

def solution(scoville, K):
	# heapify를 하면 heap정렬이 이루어짐
    heapq.heapify(scoville)
    answer = 0
    while True:
    	# 가장 작은 수를 출력
        first = heapq.heappop(scoville)
        # 시작부터 K보다 크면 바로 종료
        if first >= K:
            break
        # 끝까지 찾을 수 없다면 -1출력
        if len(scoville) == 0:
            return -1
         # 두 번째로 작은 수를 출력한다.
        second = heapq.heappop(scoville)
        # 섞은 수를 넣는다.
        heapq.heappush(scoville, first + second*2)
        answer += 1  

    return answer

결과는 군더더기 없이 깔끔하다.

나의 풀이

그런데 왜 내가 푼 풀이는 틀린 것일까 의문이 들었다. 아래는 내가 푼 풀이이다.

def solution(scoville, K):
    answer = 0
    scoville.sort()
    while(scoville[0]<K):
        if len(scoville)==1:
            return -1
        scoville[0]=(max(scoville[0],scoville[1])*2)
        +min(scoville[0],scoville[1])
        answer+=1
    return answer

heap정렬을 이용하지 않았다.
1. Sort정렬을 이용한다.
2. 제일 첫 번째 원소(가장 작은 수)와 두 번째 원소(두 번째로 작은 수)를 섞는다.
3. 이를 반복하며 K보다 커지면 종료한다.
처음에는 시간복잡도가 문제인 줄 알았으나, 원인은 2번과 3번 사이에 있었다.
max(scoville[0],scoville[1])*2을 이용해서 가장 작은 수와 가장 큰 수를 구분 했는데, 한 번 섞고나면 scoville[0]과 scoville[1]에 가장 작은 수가 있다는 보장이 되지 않는다는 것이다.

두 번째 풀이

그래서 아래처럼 작성했다.

from collections import deque
def solution(scoville, K):
    answer = 0
    scoville=deque(sorted(scoville))
    while(scoville[0]<K):
        if len(scoville)==1 :
            return -1
        scoville.append(scoville.popleft()
        				+scoville.popleft()*2)
        answer+=1
        scoville=deque(sorted(scoville))

    return answer
    

역시나 내가 생각했던 시간초과.. 이유는 시간 복잡도가 O(N^2logN)이 된다.

회고

이번 알고리즘은 해결하면서 heap에 대한 개념을 공부하는 게 되었다. (개념 참고 영상) 그리고 가장 큰 특징은 시간복잡도가 O(NlogN)라는 것과 heappop시 가장 낮은 수를 보장한다는 점이다. 주의할 점은 이는 min heap에서만이다. max heap에서는 가장 큰 수를 보장한다.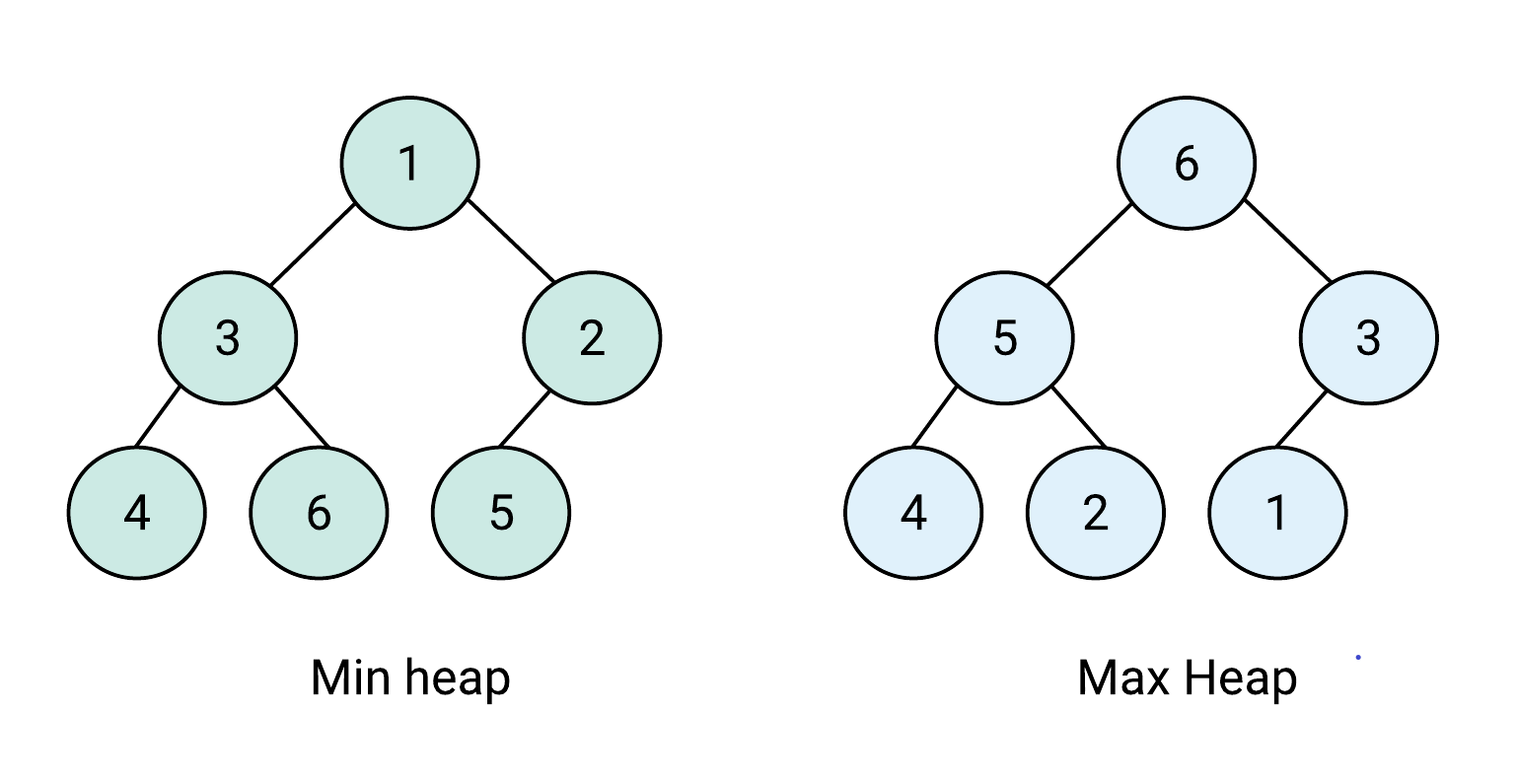사실 이 글을 쓰게 된 계기는 첫 번째 풀이가 맞았다고 가정하고 쓴 글이다.
sort 정렬 또한 시간 복잡도가 O(NlogN) 인 것으로 아는데 왜 heap은 되고 sort는 안되는가 를 파헤치려고 했었다.
근데 글을 쓰면서 분석하다 보니 원인을 파악..
while속에 sort를 넣어주어야 하는 상황이니, 이는 O(N^2logN)이 되어버린다.
그리고 오늘 알고리즘을 파헤치다 보니 추가로 알게 된 사실은 deque은 sort를 하게 되면 list가 되어버린다는 사실.. 때문에 정렬을 하면 다시 deque()을 해야 한다.

결론은 쓰다 보니 포스팅하게 됐다.