1. 문제 해석
N이 주어지고 1부터 N까지의 숫자들을 나열하여 증가하는 순열을 만든다.
예를 들어 N이 3이면, (1 2 3), (1 3 2), (2 1 3), (2 3 1), (3 1 2), (3 2 1) 으로 나열할 수 있다. 그리고 다음 입력이 2 3 1 이라면 2 3 1 다음 순열인 3 1 2를 출력한다.
3 2 1 이 입력으로 주어지면 다음 순열은 없기 때문에 -1을 출력한다.
( '10973 - 이전 순열' 문제는 반대로 입력이 2 3 1 이라면 이전 순열인 2 1 3을 출력한다. )
2. 문제 접근
N의 범위가 10,000 까지 주어졌고 시간제한은 1초이기 때문에 O(N^2)내의 알고리즘을 생각해야 한다.
처음에는 permutations을 사용했지만, 시간초과가 나왔다.
permutations의 시간복잡도는 O(N!)이기 때문이다.
3. 알고리즘 풀이
n = int(input())
arr = list(map(int, input().split()))
find = False # 순열을 찾았는지 여부
# 맨 뒤부터 시작하여 현재 원소보다 큰 값이 나올 때까지 찾음
for i in range(n-1, 0, -1):
if arr[i-1] < arr[i]: # 다음 순열이 존재할 때
# 현재 원소보다 큰 값 중 가장 오른쪽에 있는 값을 찾음
for j in range(n-1, 0, -1):
if arr[i-1] < arr[j]:
# 두 값을 교환
arr[i-1], arr[j] = arr[j], arr[i-1]
# i 이후의 값들을 오름차순으로 정렬
arr = arr[:i] + sorted(arr[i:])
find = True # 다음 순열을 찾았음을 표시
break
# 다음 순열을 찾은 경우 결과 출력
if find:
print(*arr)
else:
print(-1) # 다음 순열이 없는 경우 -1 출력
이해를 돕기위해 예를 들어 1 3 5 4 2 다음을 찾아야 한다고 가정하자.
그렇다면 출력 값은 1 4 2 3 5 가 되어야 할 것이다.
또 2 1 3 5 4가 입력으로 들어왔다고 가정해 보면,
출력 값은 2 1 4 3 5 가 되어야 한다는 것은 예상할 수 있다.
여기서 공통점을 찾아보면, 3의 자리에 4가 들어가고 그 뒤에 숫자들은 오름차순으로 정렬되었다.
즉, 뒷자리부터 확인했을 때 5까지는 증가하다가 3에서 감소하는 것을 알 수있다.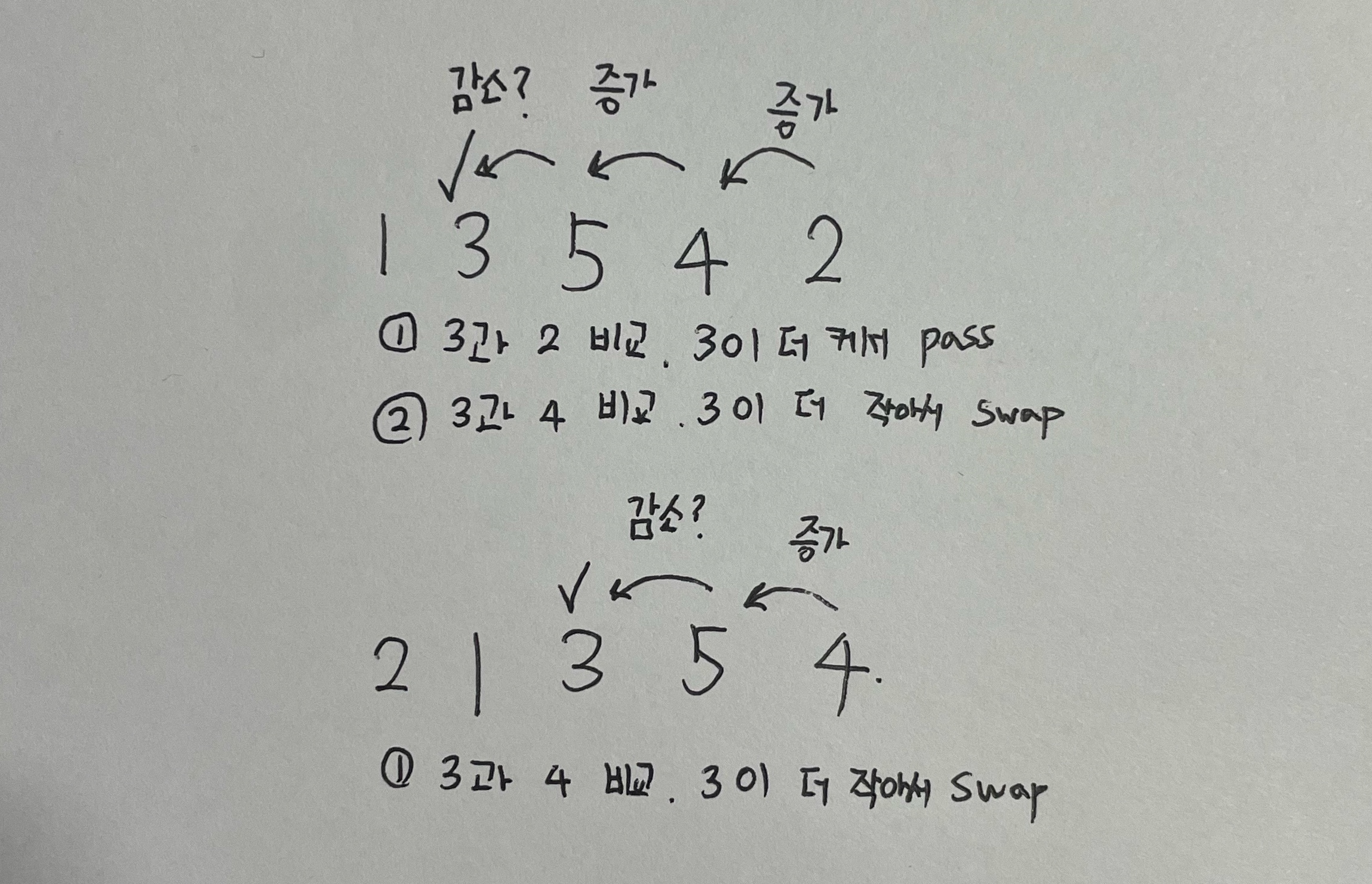 Swap을 하고 나서 바꾼 자릿수 뒤에는 오름차순으로 정렬하게 되면 다음 순열이 된다.
Swap을 하고 나서 바꾼 자릿수 뒤에는 오름차순으로 정렬하게 되면 다음 순열이 된다.
회고
아래는 처음 작성했던 코드이다.
from itertools import permutations
N = int(input())
arr = list(map(int, input().split()))
arr2 = list(range(1, N+1))
found = False
for i in permutations(arr2, N):
if found:
print(*i)
break
if arr == list(i):
found = True
else:
print(-1) 이번에 알게 된 것은
이번에 알게 된 것은 permutations 의 시간복잡도가 O(N!)이라는 사실이다. permutations 함수는 가능한 모든 순열을 생성하기 위해 입력 크기에 대해 팩토리얼적으로 증가하는 작업이 필요하다는 것을 깨달았다.
굉장히 간단한 함수라서 유용하게 사용했는데, 시간복잡도가 이렇게 큰 줄 몰랐다. N이 클수록 신경 써서 사용해야 할 것 같다.
두 번째로 for-else에 대해서 확실하게 정리한 시간이 되었다.
for-else란 for 문을 모두 돌고 나서, 아무런 출력이 없으면 else를 수행시키는 기법이다. 이를 통해서 -1을 출력하게 할 수 있었고, 코드를 한결 깔끔하게 작성할 수 있었다.
뒷자리부터 확인하는 것은 상상도 못했던 풀이이다.
아직은 백트래킹과 브루트 포스 알고리즘이 익숙하지 않아 어려움을 겪고 있다. 특히 어떤 상황에서 어떻게 적용해야 하는지에 대한 더 많은 문제를 풀어보고 학습해야 할 것같다.