1. 문제 해석
N 자리의 수가 주어지고, 각 자리가 오름차순을 이루는 오르막 수의 총 개수를 구하는 문제이다.(접한 숫자가 같을 경우에도 오름차순으로 간주)
예를 들어, N=4일 때, 1111, 1122, 1234는 모두 오르막 수
2. 문제 접근
N의 범위가 N (1 ≤ N ≤ 1,000)이 주어졌고, 이렇게 적은 범위에서는 주로 DP나 브루트 포스를 생각할 수 있는데 여기서 나는 다이나믹 프로그래밍을 사용했다.
3. 알고리즘 풀이
나열 -> 규칙 찾기 ( 점화식 )
누구나 아래까지는 나열할 수 있을 것이다.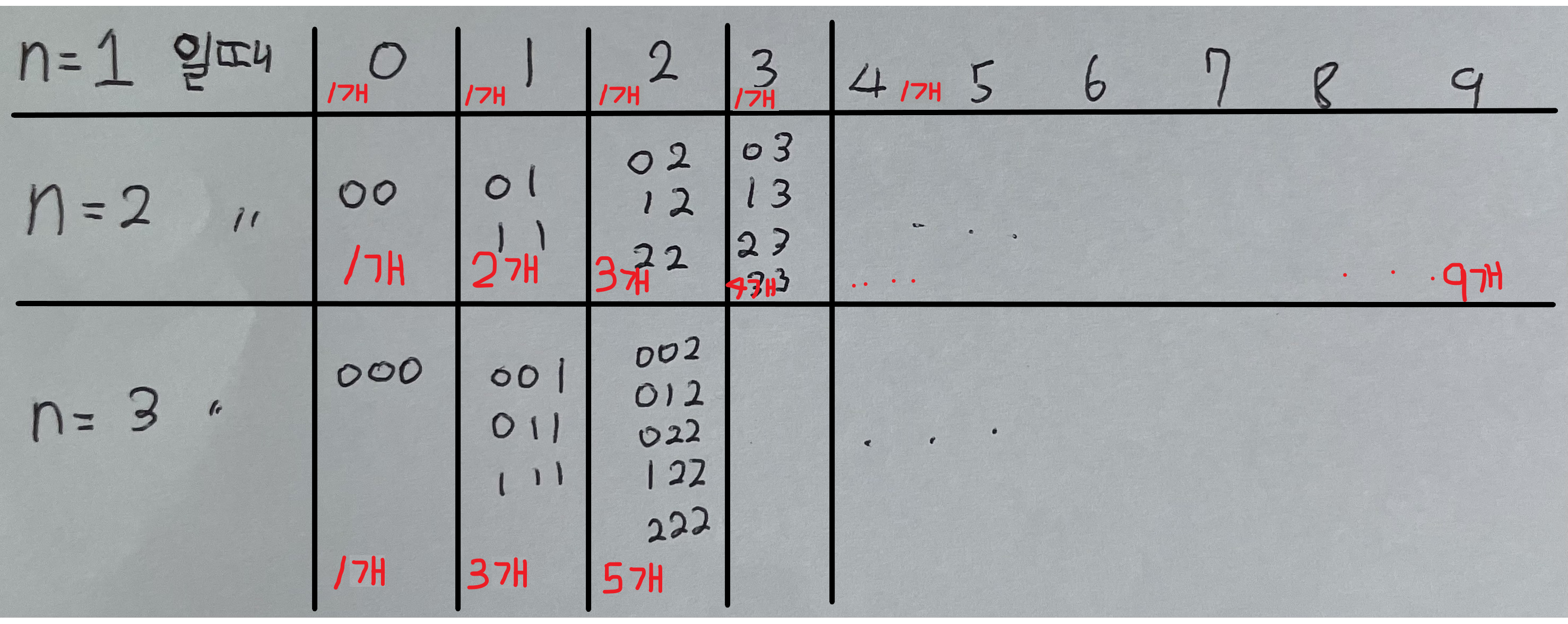
여기서 대각선 합의 규칙을 찾을 수 있다.
N=int(input())
dp=list([0]*10 for _ in range(N+1))
dp[1]=[1]*10 # 첫 행은 모두 1
for i in range(2,N+1):# 2부터 N+1까지만
for j in range(10):
if j==0: #첫 열은 모두 1
dp[i][j]=1
else:
dp[i][j]=dp[i-1][j]+dp[i][j-1]
print(sum(dp[N])%10007)(2) 리팩토링
사실 아래 코드가 풀이를 검색하면 주로 나오는 코드인데, 직관적으로 와닿지 않았다.
n = int(input())
dp = [1] * 10
for i in range(n-1):
for j in range(1, 10):
dp[j] += dp[j-1]
print(sum(dp) % 10007)왜 1차원 배열을 쓰는지와, 어떻게 dp[j] += dp[j-1] 로 한방에 정리가 되는지..
그림으로 이해하기 쉽게 설명하자면 아래와 같다.
쉽게 설명하자면, 그림처럼 바로 윗줄 행의 값을 더하면 된다는 점과
어차피 필요한 결과는 마지막 행이기에, 그 전의 행들의 값들을 저장할 필요가 없다는 것 같다.
회고
둘다 시간은 같지만, 2차원 배열보다는 1차원 배열이 공간 복잡도 측면에서 더 효율적이다.
그리고 코드도 훨씬 깔끔하다.
다만 저게 무슨 코드인지 직관적으로 알기 힘들었다.(나만 그럴수도..)
코드 깔끔 vs 누가 봐도 이해할 수 있게
후자 풀이는 코드를 보고 해설을 보면 이해가 가능하지만,
막상 시험 당일 저렇게까지 클린하게 떠올리기가 어려울 것 같다는 판단이 든다..
코딩 테스트를 준비하는 입장에서는 짧은 시간 안에 정확한 풀이를 떠올리는 능력이 중요하다.
어떻게 처리해야 하는지 고민하는 시간과 더 넓은 시야를 가져야겠다.
