비트마스크 알고리즘을 처음 들어봤다. 구글링을 해보니 흔하게 나오는데, 알고리즘을 공부하면서 처음 봄..
내용을 알아보니 대충 전자전기 수업, 디지털회로 시간에 배운 내용이다..
비트마스크란 ?
간단하게.. 이진수 표현을 이용하여 집합의 요소들의 구성을 나타내는 테크닉
대충 1010001(2) 따위를 생각하면 된다.
비트마스크를 적용하기 위해서는 비트 연산자를 알아야 한다.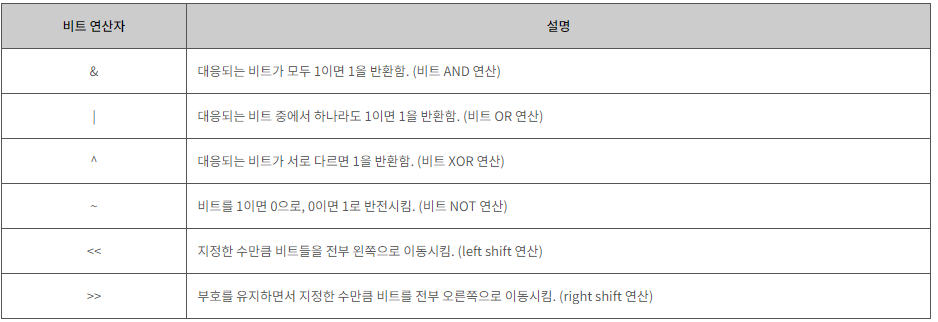
출처 : https://tcpschool.com/c/c_operator_bitwise
예시 정리는 위에 사이트에 잘 되어있다.
여기서 알고리즘에 사용되는 테크닉을 더 알아보자면,
Bit Functions이 있다.
Bit Functions
1.Get Bit
비트 연산에서 특정 위치에 있는 비트 값을 가져오는 동작이다.
예를 들면 13은 2진수로 1101(2)인데 각 자릿수가 0인지 1인지 판단하는 함수를 말한다.
우리가 1101(2) 중에서 2번 index가 1이라는 것을 확인하기 위해서는 어떻게 해야 할까? (index의 시작은 0번 부터 이다.)
1101에 0100을 AND 하면 될 것이다. 0100은 1을 << 2 한 결과가 된다.
최종적으로 1101 & (1 << 2) 가 된다.
boolean getBit(int num, int idx){
return (num & (1 << idx)
}getBit에 숫자와 알고 싶은 index의 값을 넣으면 True, False를 표현한다.
2.Set Bit
특정 위치에 있는 비트 값을 1로 설정하는 작업이다.
1001(2)이 있을 때 2번 index의 0을 1로 설정하고 싶을 때 어떻게 해야 할까?
1001에 0100을 OR하면 된다. OR은 1과 마주쳤을 때, 대상이 0이든 1이든 1의 결과를 도출하기 때문이다. 0100은 마찬가지로 1을 <<2 한 결과이다.
따라서 1001 | (1 << 2) 이다.
int setBit(int num, int idx){
return num | (1 << idx);
}3.Clear Bit
특정 위치에 있는 비트 값을 0으로 설정하는 작업이다.
어떤 값을 0으로 바꾸기 위해서는 0과 AND 작업을 하면 된다.
1001에서 3번 index인 1을 0으로 바꾸기 위해서는 0111을 & 한다.
0111은 1000의 NOT 형태이고 1000은 1<<3 한 결과이다.
최종적으로 1001 & ~(1 << 3)이다.
int cleatBit(int num, int idx){
return num & ~(1 << idx);
}4.Clear Left Bits
특정 위치를 기준으로 (본인 포함) 왼쪽에 있는 모든 비트를 0으로 설정하는 작업이다.
예를 들면 011100101(2)가 있을 때 2번 idx를 포함한 왼쪽의 모든 값을 0으로 바꾸고 싶다고 할 때 어떻게 해야 할까?
000000011(2)를 AND하면 된다. 이는 000000100 에서 1을 뺀 결과이다.
또 이는 1 << 2의 결과가 된다.
최종적으로 011100101 & ((1 << 2 ) - 1)이다.
int clearLeftBits(int num, int idx){
return num & ((1 << idx) - 1);
}5.Clear Right Bits
특정 위치를 기준으로 (본인 포함) 오른쪽에 있는 모든 비트를 0으로 설정하는 작업이다.
위와 비슷한 function이다.
011100101(2)가 있을 때 5번 idx를 포함한 오른쪽의 모든 값을 0으로 바꾸고 싶을 때 어떻게 해야 할까?
111000000(2) 를 AND하면 된다. 이는 1로 가득 찬 이진수 배열을 index + 1만큼 << 한 결과이다. 즉 111(2) << 6이다.
1로 가득 찬 이진수 배열은 -1을 의미한다.
int clearRightBits(int num, int idx){
return num & (-1 << (i + 1));
}6.Update Bit
특정 위치에 있는 비트 값을 특정 값으로 업데이트하는 작업이다.
예를 들면 110011(2)이 있을 때 2번 index의 0을 1또는 무언가로 바꾸고 싶다고 할 때 하는 작업이다.
이는 먼저 2번 index만 0인, 111011(2)을 AND하게 되면 해당 index만 0으로 바뀌고 나머지 비트들은 보존된다. 그 후 해당 index만 0이 아닌, 000y00과 OR을 하게되면, 110y11의 결과가 나온다.
int updateBit(int num, int index, boolean val){
return (num & ~(1 << index)) | ((val? 1:0) << i);
}위 내용들을 이용해서 알고리즘 문제를 풀어본다.
백준 14391 - 종이조각
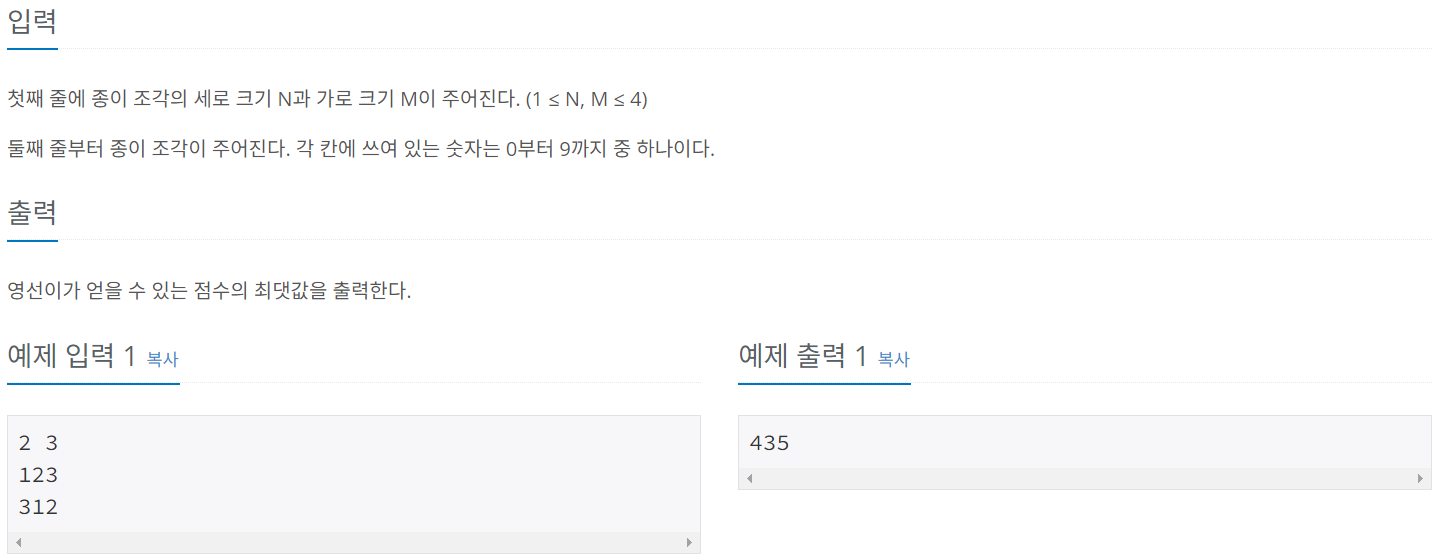
여기서 Boolean을 이용한 이유는 숫자가 연결되어 있는지를 판단한다.
가로로 연결된 경우를 1로 표기, 세로로 연결된 경우를 0으로 표기한다면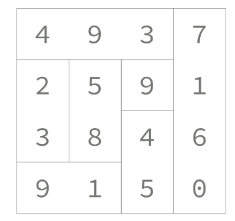
4937중에 493까지만 연결되어 있기에, 1110으로 표기한다.
2591은 0010으로 표기한다. 여기서 9는 혼자 있기에 가로로 보았을 때 연결되었다고 판단한다.
3846은 0000이고, 9150은 1100으로 표기한다.
세로를 기준으로 다시 본다.
4239는 0110, 9581은 0110, 3945는 1100으로 표기한다. 9는 혼자 있지만 가로로 보았을 때 이미 체크했기 때문에 세로로 볼 때는 연결되지 않는 것으로 본다. 마지막으로 7160은 모두 연결되어 있기 때문에 0000으로 표기한다.
# 입력을 받는다.
N,M = map(int,input().split())
arr = list(list(map(int,input().rstrip())) for _ in range(N) )
answer = []
def solution():
result = 0
for i in range(1 << N * M): # 2^(N x M)-1 의 경우의 수
total = 0
#가로, 세로 순회
for row in range(N):
rowsum = 0
for col in range(M):
idx = row * M + col
if i & (1 << idx)!=0: # 비트가 1이 아니라면 연결이 안돼있음
rowsum = rowsum * 10 + arr[row][col]
else: # 비트가 1이라면 연결되어 있음
total += rowsum
rowsum = 0
total += rowsum
for col in range(M):
colsum = 0
for row in range(N):
idx = row * M + col
if i & (1 << idx) == 0: # 비트가 0이 아니라면 연결이 안돼있음
colsum = colsum * 10 + arr[row][col]
else: # 비트가 0이라면 연결되어 있음
total += colsum
colsum = 0
total += colsum
answer.append(total) # 만들어진 수를 list에 넣어둠
return max(answer) # 가장 큰 값 반환
print(solution())회고
14391번 문제를 풀면서 처음으로 비트 마스크 개념을 접하게 되었고, 비트마스크가 문제 해결에 어떤 역할을 하는지를 알게 되었다. 디지털 논리회로 시간에 배운 내용이 섞여 있어서 이해하기는 쉬었는데, 추가적으로 bit functions이 무엇인지 알게 되었다. 비트 함수를 알게 되면서 솔루션을 보면서 이해하는 데 도움이 되었고, 정답을 얻는 데에만 집중하는 것보다 개념을 공부하고 문제에 접근하는 것이 이해를 높일 수 있다는 것을 다시 한번 깨닫는 시간이 되었다. 이번 문제는 정석적으로 비트 함수를 활용한 풀이이기 때문에 익숙해지도록 반복 학습하면 도움이 될 것 같다는 생각이 든다. 아직은 비트마스크 활용이 미숙하지만, 계속해서 학습하고 익숙해지도록 노력하는 것이 중요할 것 같다.
