
Whatnow 어플 런칭!!!!!

디프만 13기 프로젝트인 안드로이드 위치어플
약속 가는 중 친구들과 즐기는 Share-Play 서비스의 서버개발을 담당했습니다.
java 로 서버를 개발하면서 kotlin 으로 이번에 넘어오게 되면서 많은 우여곡절도 있었지만 이제는 코틀린이 너무 좋아졌달까요..ㅎ
뭐 아무튼! 저 위치 기반 서비스를 개발하면서 일반적인 거리 계산과는 다른 최적화 방법을 사용했는데요.
어떻게 도입했는지 여러분께 공유드리고자 합니다!
거리를 측정하기 위해서는 일단 S2 Geometry 를 적용시켰는데요. S2의 동작 원리를 이해하기 전에 Polygon, Polylines, Points 개념을 이해해보고 가겠습니다
Polygon, Polylines, Points란?
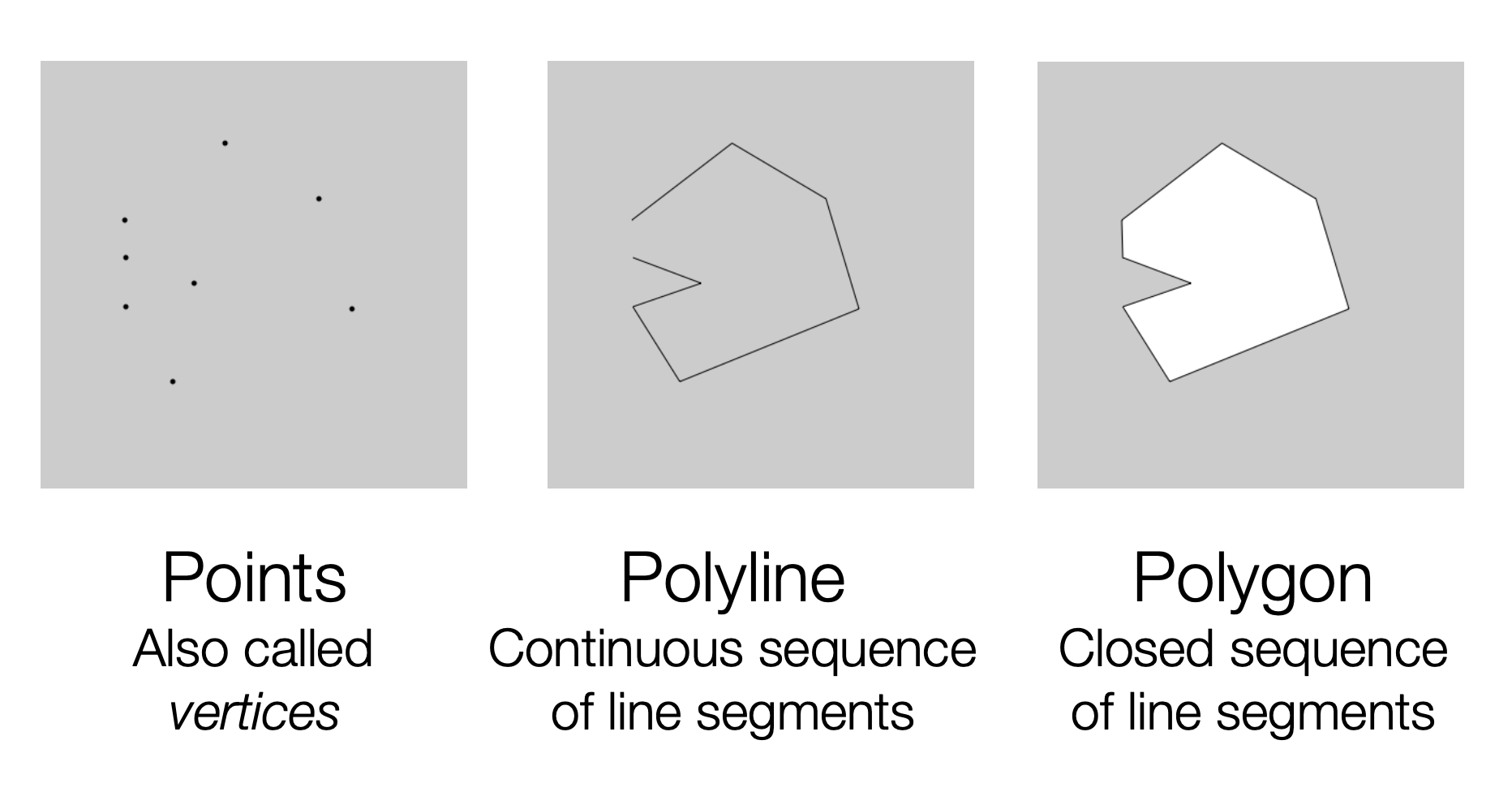
Points : 그냥 점으로 이루어진 것들
Polylines : 연속된 직선들의 집합을
Polygon : 연속된 직선들이 닫힌 형태가 (한 점으로 시작해서 같은 점으로 끝나야 한다)
곡선 표현 ( 이 세상에 곡선은 없다. )
이 개념을 이해했으니 우리는 이제 곡선을 이해해야 합니다.
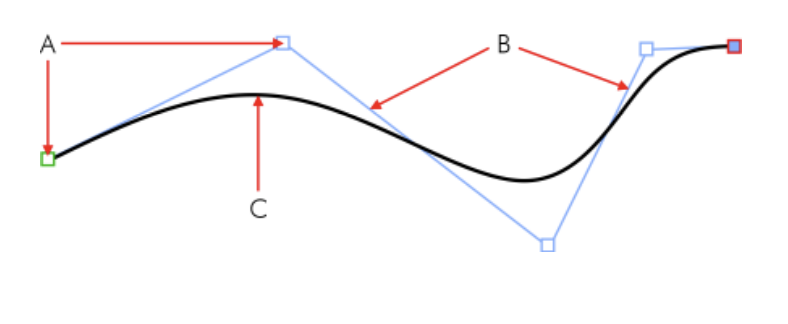
Parametric curves로 곡선을 정의하면 방정식을 개선해가면서 정의해야 하기 떄문에 엄청난 연산을 하게 됩니다. 그래서 곡선(Parametric curves)을 위 그림처럼 C 곡선을 A 직선과 B 직선으로 나눈 Polylines 의 형태로 표현하는 것이 적절합니다.
이렇게 모든 곡선은 Polylines 으로 나누어볼 수 있습니다. 이 것을 이용해서 닫힌 곡선(Parametric curves)으로 이루어진 영역 도형은 닫힌 직선(Polylines) 으로 표현할 수 있습니다. 그렇 저 B 직선을 도형 내에서는 어떻게 정의할 수 있을까요?
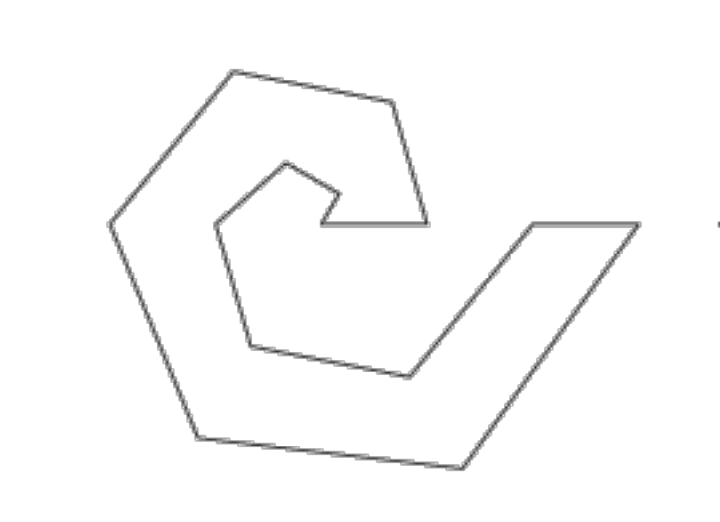
만약 영역이 정형화 되지 않고 이렇게 이상하게 생긴 도형이라면, 즉, 타원 구체인 지구를 이 모양으로 쪼갤 수 없겠죠. 그래서 모든 도형은 3각형으로 나누어야 합니다. 3각형인 이유를 증명해볼까요?
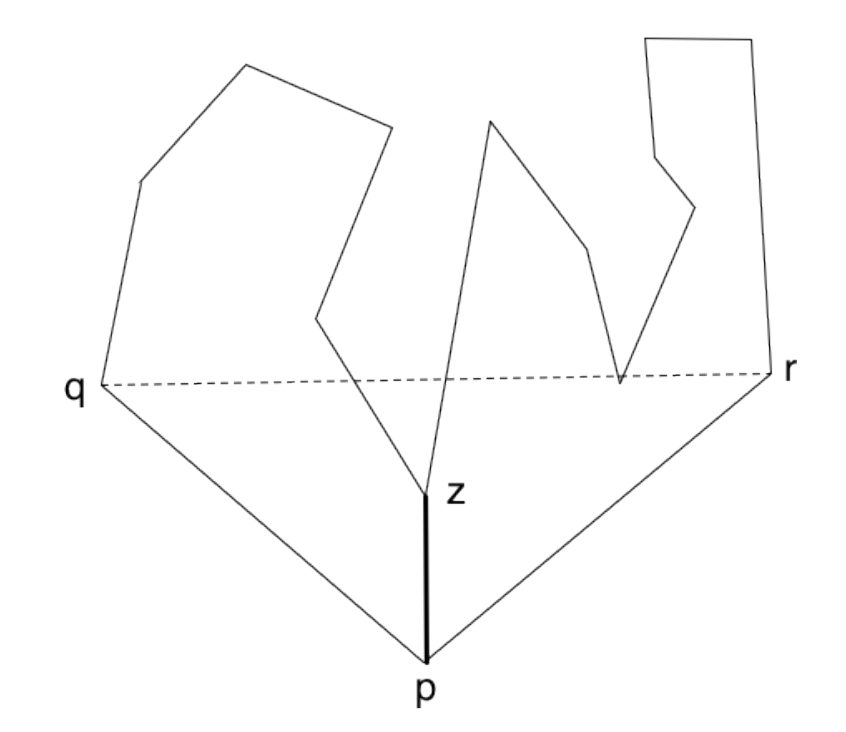
A) 볼록한 모서리 p를 골라 q와 r 를 선행과 후행으로 정의한 직선을 선택합니다.
B) qr이 대각선이면 직선 집합에 더하고. 유도하면 작은 다각형은 삼각형이 됩니다.
C) qr이 대각선이 아니라면, 내부에서 pqr삼각형 내에 있는 가장 먼 내부에서 qr까지 가장 먼 반사 꼭지점 z를 지정합니다.
D) 대각선 pz를 추가하고 pz를 기준으로 하위 다각형의 하위 다각형은 모두 삼각형이 있습니다
위 정의에 따르면 모든 다각형은 삼각형화(triangulaon) 할 수 있습니다.
이제 삼각형으로 원또한 Polygon으로 근사시켜 삼각형으로 표현할 수 있습니다.
그렇다면 S2Geometry 에서는 타원 구체인 지구를 어떻게 Polygon으로 정의했을까요?
바로 삼각형 두개를 붙인 평행 사변형으로 나누게 됩니다. 그래야 삼각형보다 교차영역을 계산하기 유리하거든요. (라고 저는 생각합니다..ㅎ)
S2Geometry
S2는 구글에서 개발한 지리 정보 시스템으로 지구를 사각형 모양인 유니크한 Cell로 분리하여 관리합니다. 위에서 언급한 것처럼 유니크한 평행 사변형으로 각 섹터를 나누게 됩니다.
| |
| 
그럼 육면체로 지구를 표현할 수 있답니다.
이렇게 나누어진 지구는 어떤 점을 찍어도 특정 영역 내부에 있다고 정의할 수 있습니다.
- S2 Cell Statistics
S2 Cell Level 입니다. 이 레벨의 단위로 지구를 사각형으로 분리할 수 있습니다.
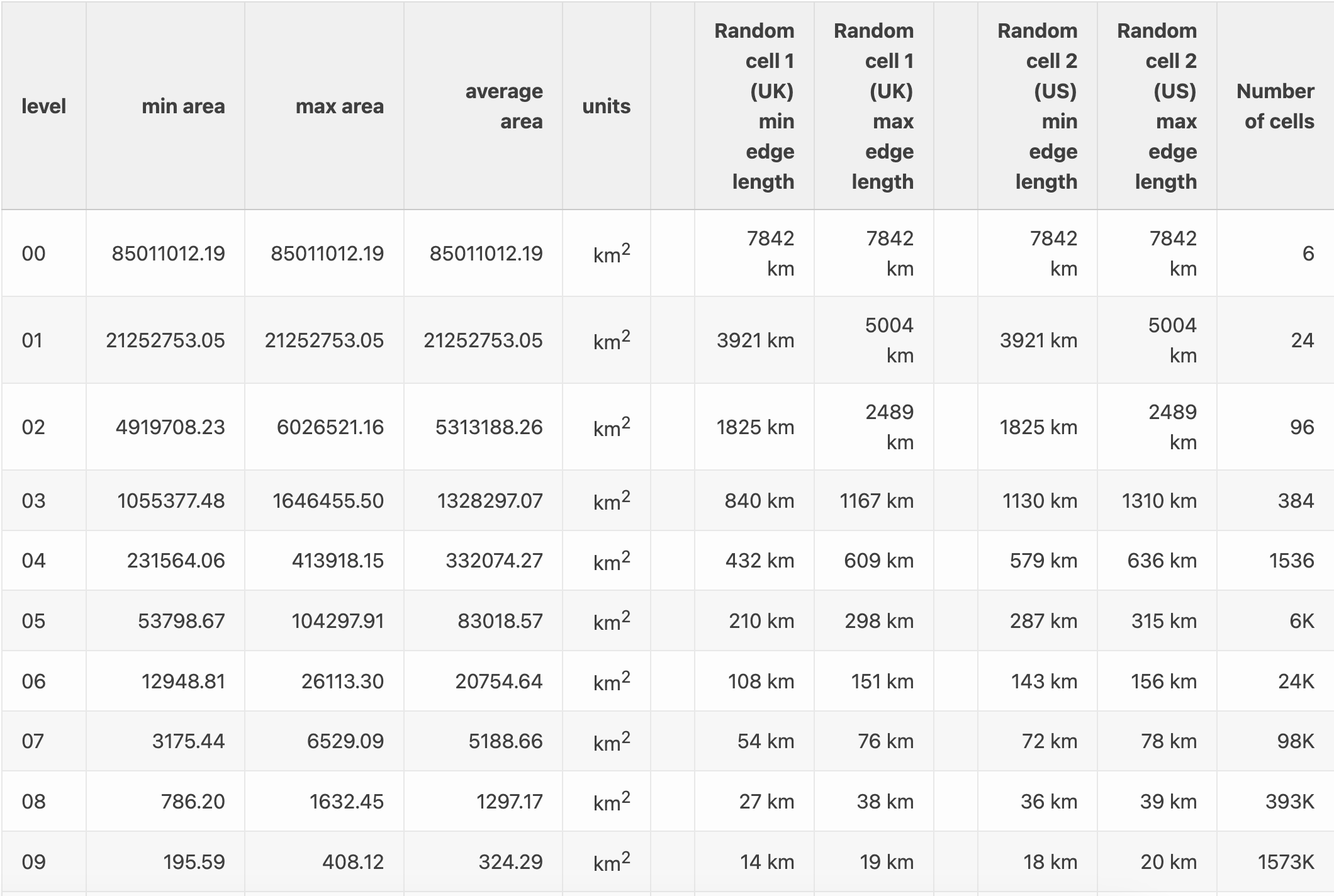
사각형의 크기가 저 level 에 따라 다른데요.
이 레벨을 조정하면

이런식으로 평행 사변형의 크기를 조절해가면서 더 세밀하게 조정할 수도 있습니다.
이제 이 사각형들을 기반으로 다양한 기능들을 구현해볼 수 있습니다.
거리를 측정했을 때
단순하게 직선인
Uclidian Distance를 사용하면 어떻게 될까요? 지구는 구형이라고 가정했을 경우 유클리디안 거리로 측정하면 아래 그림처럼 10% 정도의 오차가 발생합니다.100km 거리를 측정하는데 110km라고 나오면 엄청난 문제겠죠
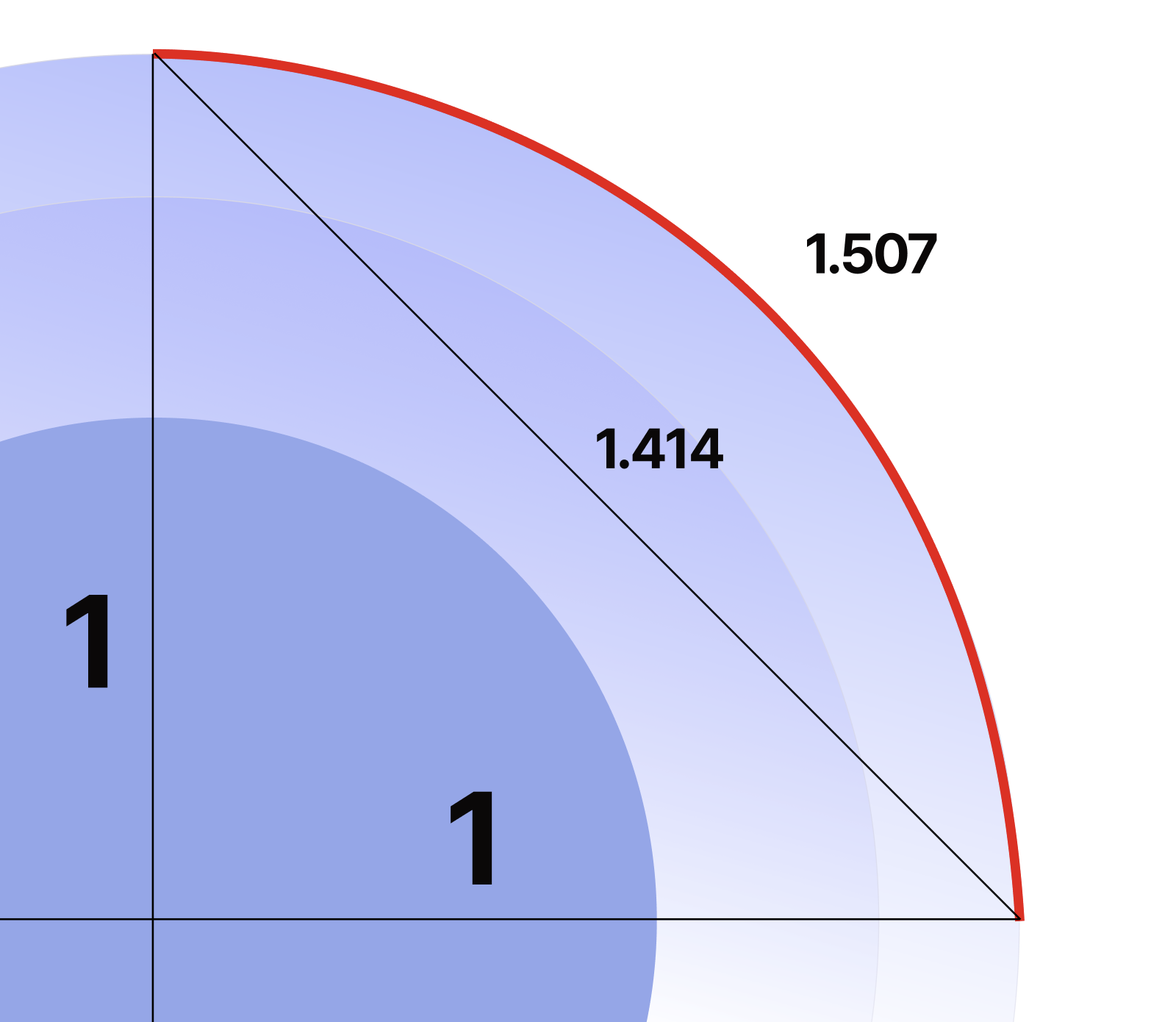
그래서 Haversine 공식의 변형을 사용해서 계산합니다.
실제 이 를 이용한 거리를 측정해서 계산한 코드를 보겠습니다.
WGS84GEO 위경도 단위로 사각형을 구해서 아래 함수를 굴리면
public S1Angle getDistance(final S2LatLng o) {
// This implements the Haversine formula, which is numerically stable for
// small distances but only gets about 8 digits of precision for very large
// distances (e.g. antipodal points). Note that 8 digits is still accurate
// to within about 10cm for a sphere the size of the Earth.
//
// This could be fixed with another sin() and cos() below, but at that point
// you might as well just convert both arguments to S2Points and compute the
// distance that way (which gives about 15 digits of accuracy for all
// distances).
// assert isValid();
// assert o.isValid();
double lat1 = latRadians;
double lat2 = o.latRadians;
double lng1 = lngRadians;
double lng2 = o.lngRadians;
double dlat = Math.sin(0.5 * (lat2 - lat1));
double dlng = Math.sin(0.5 * (lng2 - lng1));
double x = dlat * dlat + dlng * dlng * Math.cos(lat1) * Math.cos(lat2);
return S1Angle.radians(2 * Math.asin(Math.sqrt(Math.min(1.0, x))));
}
- lat1과 lng1: 첫 번째 지점의 위도와 경도를 각각 라디안 단위로 표현한 값입니다.
- lat2와 lng2: 두 번째 지점의 위도와 경도를 각각 라디안 단위로 표현한 값입니다.
- dlat: 위도 차이를 반올림하여 구한 값입니다.
- dlng: 경도 차이를 반올림하여 구한 값입니다.
- x: 위도와 경도의 차이를 이용하여 거리를 계산하기 위한 중간값입니다.
최종 거리 계산:
x 값을 제곱근 씌운 후, 이 값이 1.0보다 크면 1.0으로 설정합니다. 이는 x 값이 정확히 1보다 큰 경우 제대로된 거리 계산을 위해 값을 조정하는 과정입니다.
Math.asin() 함수를 사용하여 제곱근 값을 역사인 함수로 변환한 후, 2를 곱하여 라디안 단위의 거리를 계산합니다.
이 과정을 통해서 거리를 계산했습니다.
fun isArrived(promiseUser: PromiseUser, destination: CoordinateVo): Boolean {
val start = S2LatLng.fromDegrees(promiseUser.userLocation!!.latitude, promiseUser.userLocation!!.longitude)
val destination = S2LatLng.fromDegrees(destination.latitude, destination.longitude)
val distanceInMeters = start.getDistance(destination).radians() * RADIUS_EARTH
return distanceInMeters < RADIUS_ARRIVED_DESTINATION
}그래서 위 코드에 대한 테스트 코드를 통해 검증해보도록 하겠습니다.
1. test 15미터일때, 10미터 이내인지 테스트
@Test
fun `500미터 안에 인접해 있으면 도착했다 정의`() {
val a = PromiseUser(userLocation = CoordinateVo(35.866334, 127.146223), promiseId = 1L, userId = 1L)
val b = CoordinateVo(35.866339,127.146392)
// 실제 거리 : 15 m
// when and return
val arrived = promiseUserDomainService.isArrived(a, b)
assertEquals(true, arrived)
}
2. test 9미터일때, 10미터 이내인지 테스트
@Test
fun `500미터 안에 인접해 있으면 도착했다 정의`() {
val a = PromiseUser(userLocation = CoordinateVo(35.866334, 127.146223), promiseId = 1L, userId = 1L)
val b = CoordinateVo(35.866328, 127.146327)
// 실제 거리 : 9 m
// when and return
val arrived = promiseUserDomainService.isArrived(a, b)
assertEquals(true, arrived)
}
네 생각보다 잘 동작하네요ㅎㅎ
다음 포스팅에는 GeoHash 를 이용하여 실제 계산이 아니라 문자열 비교를 통해 더 빠르게 거리를 측정해보도록 하겠습니다.
reference
