LCS

LCS의 두가지 의미

Longset Common Substring과 Longest Common Subsequence 두가지 의미가 있다,

둘이 꽤 다르다.

Longset Common Substring

최장 공통 문자열을 의미한다.

예를들어서, ABCDEF 와 GBCDFE가 있다면, 최장 공통 문자열은 BCD이다. 즉, 연속된 '문자열'중 가장 긴 것을 찾는 문제이다.

이를 점화식으로 나타내면 다음과 같다.

if (i == 0 || j == 0):
	dp[i][j] = 0
else if (strA[i] == strB[j]):
	dp[i][j] = Ldp[i - 1][j - 1] + 1 // 대각선 한칸 뒤는 바로 자기 전 자리
else:
	dp[i][j] = 0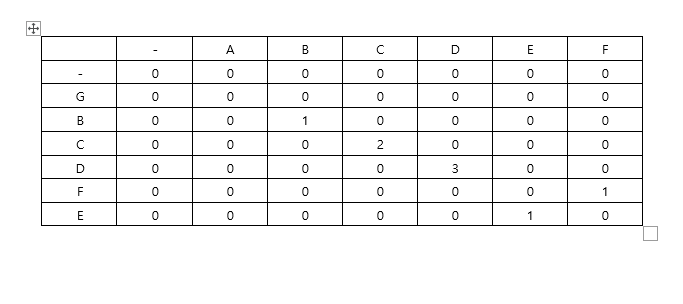

직접 그려보면 다음과 같다.

생각보다 쉬운 문제이다

Longest Common Subsequence

최장 공통 부분수열을 구하는 문제이다. 연속될 필요가 없다. 따라서 점화식도 조금은 변해야한다. 이전 자리수의 수열길이를 다음 자리수도 그대로 가지고 가야하는것이다 .

if (i == 0 || j == 0) dp[i][j] = 0;
else if (strA[i-1] == strB[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
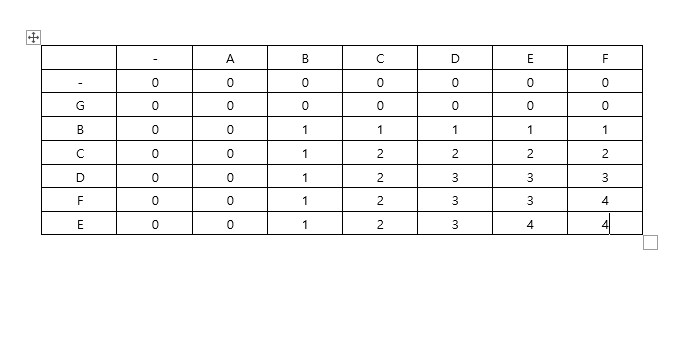
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);

우선 계산의 용이함을 위해서 0자리수는 전부 0으로 채운다.

그리고 만약 두 수가 같다면, 대각선 자리(문자열 자기 바로 전 자리)에서 1을 더한다.

그렇지 않은 경우는, 현재 위치의 바로 전 문자, 혹은 자기 자신의 이전값을 가지고 와서 더 큰 값을 집어넣는다.

전체 코드는 다음과 같다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;

string strA, strB;

int main() {
    cin >> strA >> strB;
    int len_a = strA.size();
    int len_b = strB.size();
    int dp[len_a + 1][len_b + 1];

    for (int i = 0; i <= len_a; i++) {
        for (int j = 0; j <= len_b; j++) {
            if (i == 0 || j == 0) dp[i][j] = 0;
            else if (strA[i-1] == strB[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
            else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
        }
    }

    int max_num =  0;
    cout << dp[len_a][len_b];
}

i는 계산상 편의를 위해 1씩 늘어나있다. 따라서 str에 적용할 때는 1씩 빼서 적용해야한다.

정리

알면 쉽지만 모르면 어려운 그런 문제이다

알고 넘어가자