이번 글은 아래의 책을 읽고 새롭게 알게된 점과 예상 면접 문제를 정리한 글이다.

한 권으로 읽는 컴퓨터 구조와 프로그래밍: 더 나은 소프트웨어 개발을 위한 하드웨어, 자료구조, 필수 알고리즘 등 프로그래머의 비밀 노트
1장 컴퓨터 내부의 언어 체계_컴퓨터는 어떤 말을 사용할까
1-1. 언어랑 무엇인가
1-2. 문자 언어
1-3. 비트
1-4. 논리 연산
1-5. 정수를 비트로 표현하는 방법
1-6. 실수를 표현하는 방법
1-7. 2진 코드화한 10진수 시스템
1-8. 2진수를 다루는 쉬운 방법
1-9. 비트 그룹의 이름
1-10. 문자를 사용한 수 표현
1-11. 색을 표현하는 방법이번 장 요약
📌 비트가 무엇이고, 비트로 무엇을 할 수 있는지에 대해서
새롭게 알게된 것
62쪽
2진수 덧셈
덧셈 결과가 우리가 사용할 비트의 개수로 표현할 수 있는 범위를 벗어나면 어떻게 해야할까? 이런 경우 오버플로overflow가 발생한다. 오버플로란 말은 MSB(M Bit)에서 울림이 발생했다는 뜻이다.
(중략)
나중에 자세히 보겠지만 컴퓨터에는 조건 코드(또는 상태 코드) 레지스터condition code register라는 것이 있어서 몇 가지 이상한 정보를 담아둔다. 이런 정보 중에는 오버플로 비트overflow bit가 있고, 이 비트에는 MSB에서 발생한 올림값이 들어간다. 이 비트값을 보면 오버플로가 발생했는지 알 수 있다.
69쪽
고정소수점 표현법
이런 접근 방법이 잘 작동하기는 하지만, 쓸모 있는 범위의 실숫값을 표현하기 위해 필요한 비트 개수가 너무 많기 때문에 범용 컴퓨터에서 이런 방식을 사용하는 경우는 드물다. 디지털 신호 처리 장치DSP, digital signal processor 등 특별한 목적에 쓰이는 일부 컴퓨터는 여전히 고정소수점 수를 쓰기도 한다.(11장에서 계속)
73쪽
IEEE 부동소수점 수 표준
IEEE 754에서 편리한 점은 0으로 나눴을 때 생길 수 있는 야으이 무한대가 음의 무한대를 표현하는 비트 패턴 등 여러 가지 특별한 비트 패턴을 제공한다는 점이다. 이런 비트 패턴 중에는 ‘수가 아님not a number’이라는 뜻의 NaN을 표현하는 특별한 값도 있다. 이로 인해 부동소수점 수로 계산을 하던 도중에 NaN 값이 생기면 뭔가 잘못된 산술 연산을 수행했다는 뜻이다. 이런 특별한 비트 패턴들은 앞에서 이야기한 특별한 지숫값(모든 비트가 0이거나 모든 비트가 1인 지수)을 사용한다.
2진 코드화한 10진수 시스템
오래된 컴퓨터들은 BCDbinary-coded decimal 수를 처리하는 방법을 알고 있었다. 하지만 이런 시스템은 더 이상 주류에 남아 있지 않다. 하지만 BCD가 튀어나오는 경우가 자주 있기 때문에 이에 대해 알아두면 좋다. 특히 컴퓨터와 상호작용하는 장치 중에서 디스플레이나 가속도 센서 등이 BCD를 사용하는 경우가 있다.
76쪽
프로그래밍 언어의 진법 표기법
여러 프로그래밍 언어에서는 다음과 같은 표기법을 따른다.
∙ 0으로 시작하는 숫자는 8진 숫자다. 예를 들어, 017은 8진수이며 값은 10진수로 15다.
∙ 1부터 9 사이의 숫자로 시작하는 숫자는 10진수다. 예를 들어 123은 10진수다.
∙ 0x가 앞에 붙은 (접두사) 숫자는 16진수다. 예를 들어, 0x12f는 16진수이며 값은 10진수 303이다.
81쪽
텍스트 표현 > 다른 표준의 진화
비트 가격이 떨어짐에 따라 유니코드Unicode라는 새로운 표준이 만들어졌고, 문자에 16비트 코드를 부여했다. 유니코드가 생긴 당시에는 16비트면 지구상에 있는 모든 문자를 다 담고도 여분이 남으리라 생각했다. 그 후 유니코드는 21비트(그중 1,112,064가지 값이 문자를 표현한다)까지 확장됐으며, 그 정도면 앞으로 모든 문자를 다 표현할 수 있을 것이다. 하지만 이렇게 확장하더라도 어쩌면 새로운 고양이 이모티콘을 만들고 싶은 인간의 욕구를 다 담기엔 충분하지 않을 수도 있다.
85쪽
베이스64 인코딩
이 인코딩 방식은 여전히 전자우편 첨부파일 전송에 많이 사용 중이다.
궁금한 것
유니코드 변환 형식 8비트에서 왼쪽의 MSB가 자리수를 채우는 방법에서 8비트 중 5비트만 쓸거면 3비트에다가 끝날 때까지 1을 채우고 0으로 끝나는 것을 표현하는 건가?
👉 맞다!
예상 문제
자바스크립트에서
let x = 1.1;
let y = 0.1;
x+y === 1.2 마지막 결과가 false인 이유는 무엇일까요?
(다른 언어도 마찬가지예요)
답
IEEE 부동소수점 수 시스템은 컴퓨터에 실수를 표현하는 표준 방법이다. 32비트에 가장 왼쪽부터 1비트에 부호, 8비트는 지수, 23비트는 가수가 할당됩니다. 그런데 0.1의 경우 이진법으로 변환할 때 가수 부분이 순환소수가 되고 23비트를 넘은 부분은 할당되지 않는다. 따라서 정확한 소수로 계산되지 않기 때문에 컴퓨터 상에서는 다음과 같은 계산 오류가 발생합니다.
계산 정밀도를 높이기 위해서는 최대한 소수 사용을 지양하거나, 64비트를 사용하는 2배 정밀도 수(double)를 사용하여 더 넒은 범위의 수를 표현할 수 있다.
(출처: 위 수식이 틀린 이유는? (개발자 면접 타임))
(출처: 스터디 도서 71쪽)
자바스크립트에서 for문을 이용하여 다음과 같이 출력되는 제어문을 만드세요.
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9답
<헷갈리는 오답>
for (let i = 0.1; i < 1; i+=0.1){
console.log(i)
}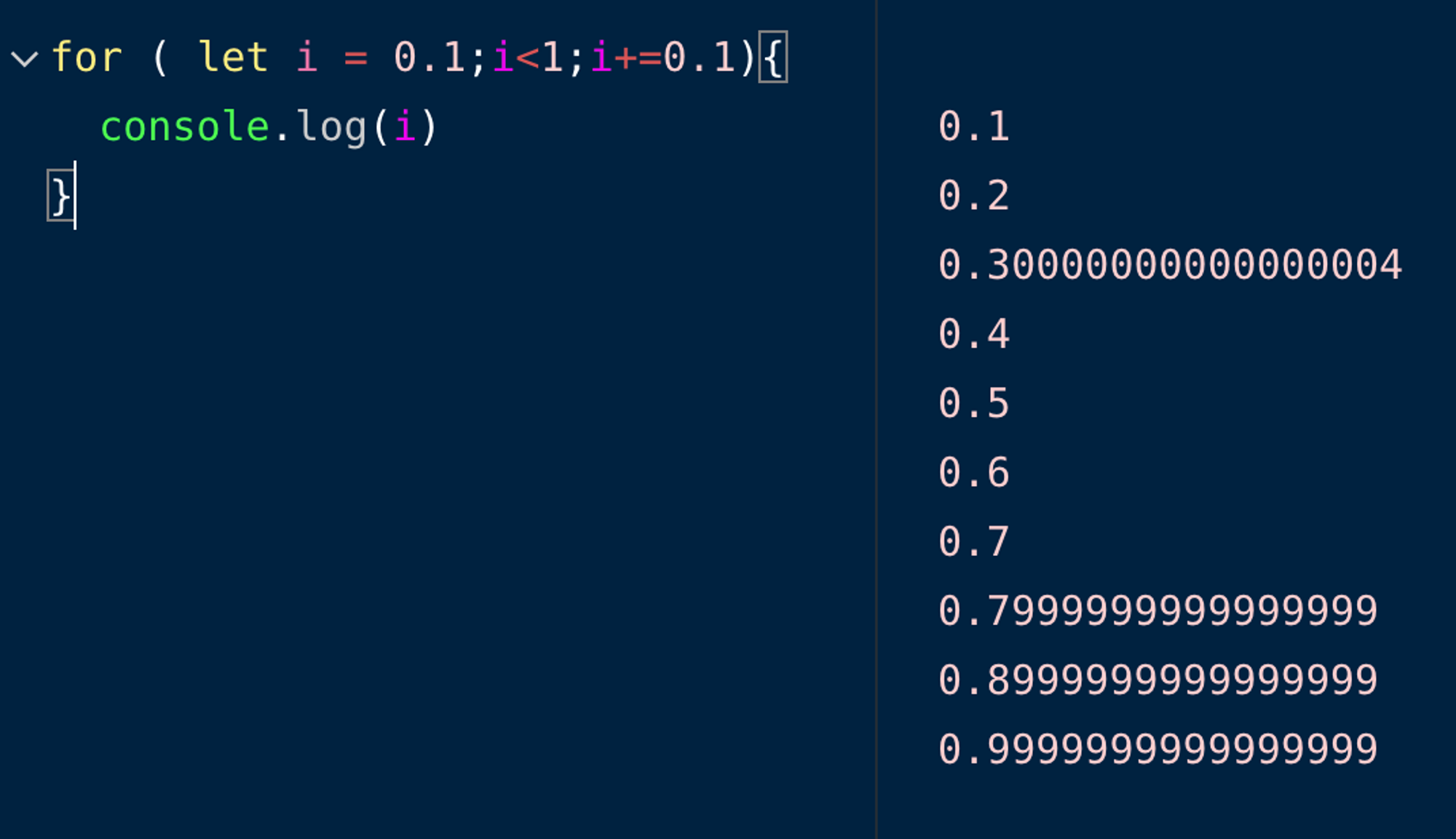
?! 위에서 언급했던 부동소수점 문제로 인해서 원하는 답이 나오지 않는다!
그래서 웬만해서 소수점 할당은 안하는 것이 좋다.
<답>
for ( let i = 1; i<10 ; i++){
console.log(parseFloat('0.'+i.toString()))
}32 비트 운영체제에서 3TB 하드디스크의 용량을 2TB로 인식하거나 오류가 발생하는 이유는 무엇일까요?
답
32비트를 사용하여 나타낼 수 있는 최대 수는 4,294,967,295이므로 512바이트 섹터(약 2.2TB)를 사용하여 2.199TB의 용량으로 변환된다. 따라서 이를 초과하는 용량은 컴퓨터의 정수 연산의 계산 결과가 허용 범위를 초과할 때 발생하는 오류인 오버플로overflow가 발생하여 주소 지정이 불가하기 때문에 3TB의 하드디스크를 2TB로 인식한다.
(출처: Why can't you access over 2 TB of data using a 32-bit operating system?)
(출처: 2TB보다 큰 하드 디스크에 대한 Windows 지원)
(출처: 용량 크다고 무턱대고 샀다간…아차! - 3TB 하드디스크에 숨은 ‘함정’)
Base64를 사용하는 이유는 무엇일까요?
답
Base64는 바이너리 데이터를 아스키 모드 일부와 일대일 매칭되는 문자열로 단순 치환하는 인코딩 방식이다. 치환한 데이터의 길이는 기존 데이터 길이보다 약 30% 정도 늘어나는 단점이 있지만, 이를 사용하는 가장 큰 이유는 바이너리 데이터를 문자열 기반 데이터로 취급할 수 있기 때문이다. 이미지를 포함하는 대부분의 파일은 UTF-8 형식 또는 아스키 코드가 아니기 때문에 JSON과 같은 문자열 기반 데이터 형식에서 UnicodeDecodeError가 발생할 확률이 높다. 이를 Base64로 인코딩하면 UTF-8과 호환 가능한 문자열을 얻을 수 있다.
(출처: 이기곤, ‘학교에서 알려주지 않는 17가지 실무 개발 기술’, 한빛미디어, 202쪽)
❓ 추가 꼬리 질문
Base64에서 패딩(’=’, ‘==’)을 추가하는 이유는 무엇일까요?
👉 답
데이터 길이를 명시적으로 구분할 수 있는 JSON이나 HTTP 바디와 같은 곳에서는 필요하진 않지만 TCP처럼 스트림 형태로 데이터를 주고받는 환경에서는 패딩이 없는 데이터를 받을 때 문제가 될 수 있다.
네트워크 프로토콜로 데이터를 3바이트씩 끊어서 Base64를 디코딩하는 상황에서 패딩이 있을 때는 실질적인 데이터는 1바이트지만 패딩을 포함해서 3바이트를 전송해 올바른 데이터로 볼 수 있지만 패딩이 없다면, 네트워크 패킷을 읽는 서버는 3바이트를 채우기 위해 다음 스트림이 올 때까지 기다려야 하는지, 이번에 받은 1바이트를 그대로 디코딩해야 하는지 명확히 알 수 있는 방법이 없기 때문이다.
(출처: 이기곤, ‘학교에서 알려주지 않는 17가지 실무 개발 기술’, 한빛미디어, 206쪽)
느낀 점
이번 CS 책은 읽기 시작하는 것조차 용기가 필요했다.
600쪽이 넘는 책 두께에 압도당하고,
무엇보다 항상 비트 얘기만 나오면 오들오들 떨면서 숨던 나였기에...
시작부터 비트부터 이야기했어서 1장부터 부담이 컸다.

그런데 왠걸! 너무 재밌게 읽었다.
이해도 정말 쉽게 되고, 이전에 배웠던 것을 하나하나 갖고 와서 연결하는 것도 재밌었다.
그리고 컴퓨터가 2진수밖에 읽지 못하는 것이... 지금와서 생각해보면 참 바보같다는 생각이 들었다.(2진수밖에 모르는 컴퓨터 바보!)
예상 면접 문제에서도 논했듯이 소수점 계산이 예상되로 되지 않는데, 관련해서 정확도를 높이는 해결 방법이 메모리 공간을 늘리는 것 말고는 연산할 때 직접 조작하는 것밖에 없다니!
바보같은 의문일 순 있지만 컴퓨터는 왜 10진수가 아닌걸까?
다음 장은 전자 회로의 조합 논리에 대해서 이야기하는데 조금 더 하드웨어적인 부분인 것 같다. 기대된다!
