DFS(Depth-First Search)

DFS는 깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.

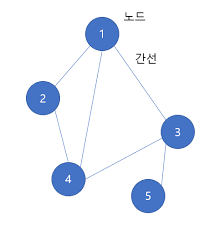
DFS를 이해하기에 앞서 그래프의 기본구조에 대해서 알아야 한다. 그래프는 기본적으로 노드와 간선으로 표현이 되며 두 노드가 간선으로 연결되어 있을때, 이 두 노드는 인접하다 라고 표현할수 있다.

그래프의 표현방식에는 인접 행렬과 인접 리스트가 존재한다. 이번 포스트에서는 따로 인접 행렬과 인접 리스트에 대한 설명은 하지 않는다. 단, 특정한 노드와 연결된 모든 인전 노드를 순회해야하는 경우, 인접 리스트 방식이 인접 행렬 방식에 비해 메모리 공간의 낭비가 적다는 것만 기억하자.

DFS의 구현에는 스택 자료구조가 사용되며, 다음의 동작 순서를 가진다.

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

위의 그래프를 통해 DFS의 동작을 알아보자.

1. 시작 노드인 '1'을 스택에 삽입후 방문 처리 한다.
   스택: 1
2. 스택의 최상단 노드 '1'에 방문하지 않은 인접노드 '2','3','4'가 있고 이중 가장 작은 노드 '2'를 스택에 넣고 방문 처리 한다.
   스택: 1 2
3. 스택의 최상단 노드 '2'에 방문하지 않은 인접노드 '4'가 있고 똑같이 스택에 삽입 후 방문 처리 한다.
   스택: 1 2 4
4. 스택의 최상단 노드 '4'에 방문하지 않은 인접 노드 '3'을 스택에 삽입하고 방문처리 한다.
   스택: 1 2 4 3
5. 스택의 최상단 노드 '3'에 방문하지 않은 인접 노드 '5'를 스택에 삽입하고 방문처리 한다.
   스택: 1 2 4 3 5
6. 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 수행을 종료한다.

이런 수행을 거쳐 탐색된 순서는 1->2->4->3->5 가 된다.

이제 코드로 구현해 보자.

def dfs(graph, v, visited):
	visited[v] = True
    print(v, end=" ")
    for i in graph[v]:
    	if not visited[i]:
        	dfs(graph, i, visited)
graph = [
	[],
    [2,3,4],
    [1,4],
    [1,4,5],
    [1,2,3],
    [3]
]

visited = [False]*6
dfs(graph, 1, visited)