정규화
관계형 데이터베이스의 설계에서 중복을 최소화하게 데이터를 구조화하는 프로세스기본 목표: 관련이 없는 함수 종속성은 별개의 릴레이션으로 표현
장점
- 이상 현상의 발생 가능성을 줄여준다.
- 테이블 간의 중복된 데이터를 허용하지 않아 무결성을 유지할 수 있다.
- DB의 저장 용량을 줄일 수 있다.
단점
- 연산 시간이 증가한다.
정규화의 탄생배경
한 릴레이션에 여러 Entity의 Attribute들을 혼합하게 되면 중복 저장되며, 저장공간을 낭비하게 된다.
또한 중복된 정보로 인해 '갱신 이상' 이 발생하게 된다.
동일한 정보를 한 릴레이션에는 변경하고, 나머지 릴레이션에서는 변경하지 않은 경우 어느 것이 정확한지 알 수 없게 된다.
이런 문제를 해결하기 위해 정규화 과정을 거친다.
정규화 과정을 거치게되면 정규형을 만족하게 된다.
정규형
- 특정 조건을 만족하는 릴레이션의 스키마의 형태
- 제 1 정규형, 제 2 정규형, 제 3 정규형, BCNF형, 제 4 정규형, 제 5 정규형이 존재
- 차수가 높아질수록 만족시켜야 할 제약 조건이 늘어난다.
정규화의 종류
제 1 정규화
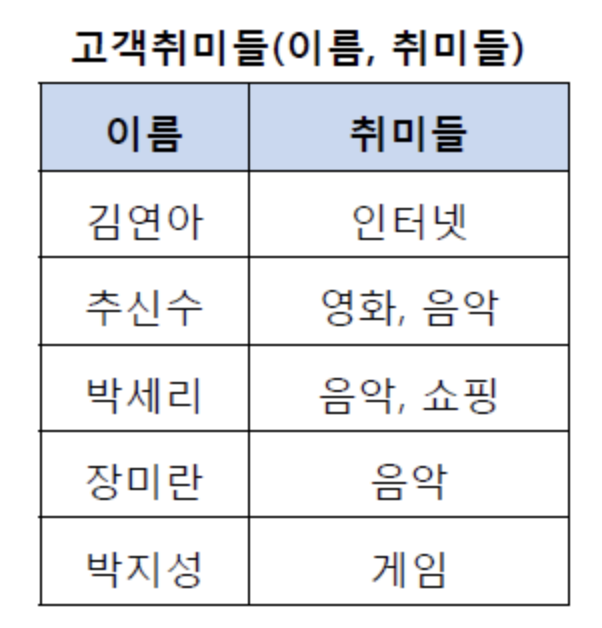
테이블의 컬럼이 원자값을 갖도록 테이블을 분해하는 것예제)
위와 같은 테이블은 추신수, 박세리는 여러개의 취미를 갖고 있어 제 1 정규형을 만족하지 않는다.
위의 테이블을 제 1 정규화를 진행하면 밑과 같은 사진이다.
제 2 정규화
제 1 정규화를 진행한 테이블에 대해 완전 함수 종속을 만족하도록 테이블을 분해하는 것함수 종속: 기본 키의 부분집합이 결정자가 되어선 안된다는 것을 의미
예제)
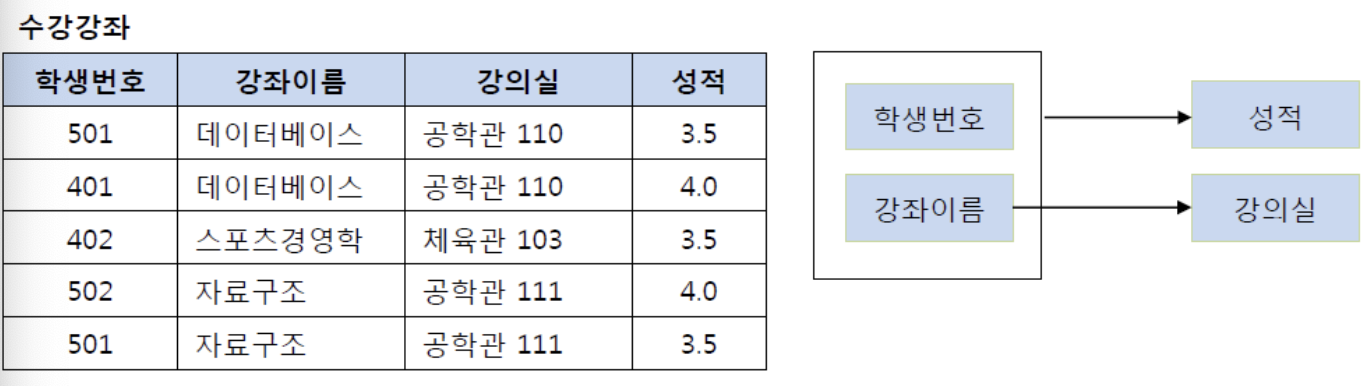
- 위 테이블의 기본키: (학생번호, 강좌이름) -> 복합키
- (학생번호, 강좌이름)인 기본키는 성적을 결정: (학생번호, 강좌이름) => 성적
- 강의실이라는 컬럼은 기본키의 부분집합인 강좌이름에 의해 결정 (강좌이름) => 강의실
즉 기본키(학생번호, 강좌이름)의 부분키인 강좌이름이 결정자이기 때문에 기존의 테이블에서 강의실을 분해하여 별도의 테이블로 관리하여 밑의 사진과 같이 제 2 정규형을 만족시킬 수 있다.
제 3 정규화
제 2 정규화를 진행한 테이블에 대해 이행적 종속을 없애도록 테이블을 분해하는 것이행적 종속: A -> B, B -> C 가 성립할 때 A -> C 가 성립되는 것
예제)
- 위의 테이블에서 학생번호는 강좌이름을 결정하고, 강좌이름은 수강료를 결정하고 있다.
이를 밑의 그림과 같이 (학생번호, 강좌이름) 테이블과 (강좌이름, 수강료) 테이블로 분해해야 이행적 종속이 제거되어 제 3 정규형을 만족시킨다.
이행적 종속을 제거하는 이유
예를 들어 501번 학생이 수강하는 강좌가 스포츠경영학이라는 수업으로 변경되었다.
이 때 이행적 종속이 존재한다면 501번의 학생은 강좌이름과 수강료 모두 변경해줘야하지만 이를 제거해준다면 번거로움이 해결된다.
BCNF 정규화
제 3 정규화를 진행한 테이블에 대해 모든 결정자가 후보키가 되도록 테이블을 분해하는 것예제)
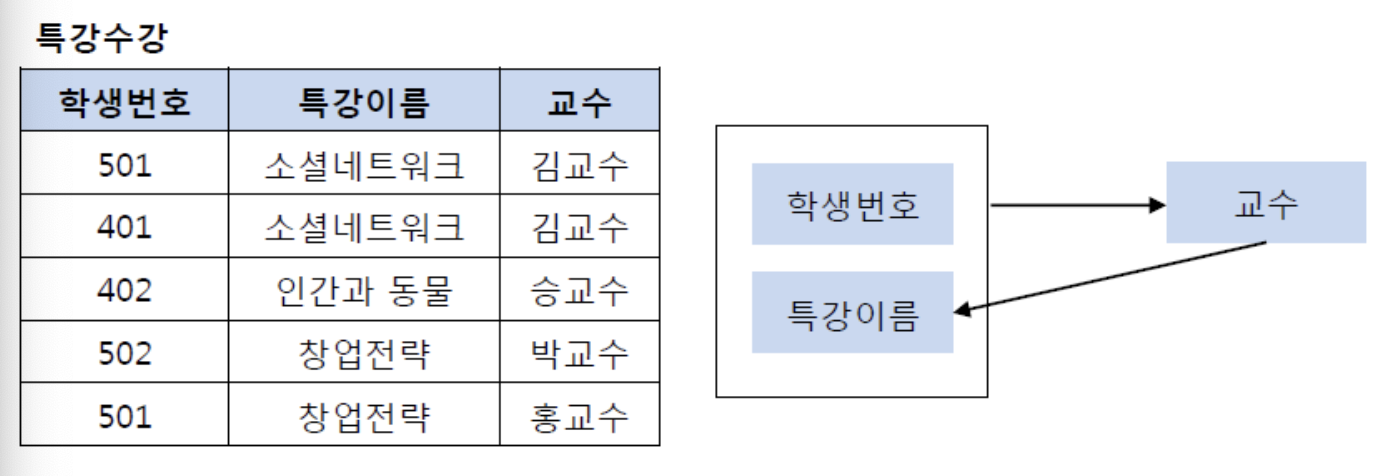
기본키: (학생번호, 특강이름)
- 기본키(학생번호, 특강이름)는 교수를 결정
- 교수는 특강이름을 결정하지만 후보키가 아님
밑의 그림과 같이 BCNF 정규형을 만족하게 특강신청 테이블과 특강교수 테이블로 분해할 수 있다.
제 4 정규화
BCNF 정규화를 진행한 테이블에 대해 값을 여러개 갖는 릴레이션을 분해하여 애트리뷰트가 원자값을 갖도록 하는 것다치 종속성: 두개의 독립된 애트리뷰트가 1:N 관계로 대응하는 관계
( ->> 로 표기)
예제)
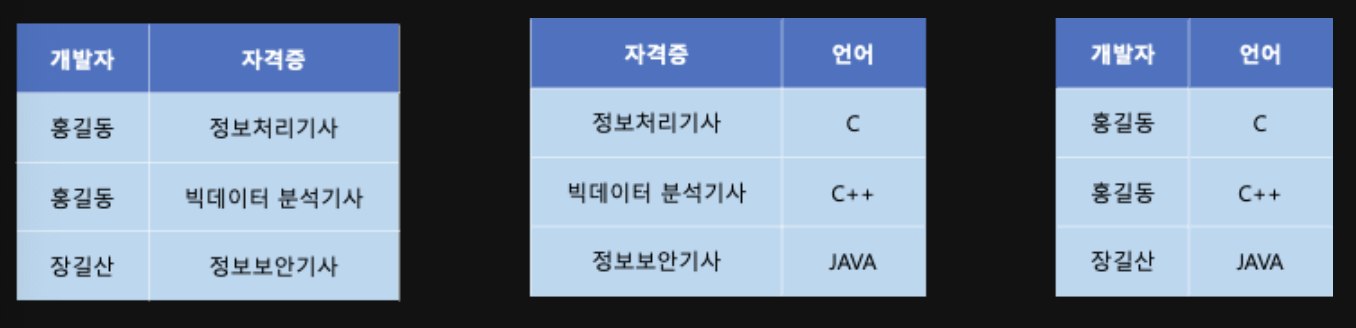
위의 테이블은 개발자 ->> 자격증 과 개발자 ->> 언어 두 가지 의존성을 가지므로 다치 종속이 존재한다.
밑의 그림과 같이 제 4 정규형을 만족하게끔 개발자-자격증 테이블과 개발자--언어 테이블로 분해할 수 있다.
제 5 정규화
제 4 정규화를 진행한 테이블에 대해 조인 종속이 없게 끔 테이블을 분리한 것조인 종속: 하나의 릴레이션을 여러개의 릴레이션으로 분해했다가, 다시 조인했을 때 데이터 손실이 없고 필요없는 데이터가 생기는 것
예제
위의 테이블은 제 4 정규화가 된 테이블에 조인 연산을 수행한 테이블이다.
데이터 손실은 없지만 필요없는 데이터가 추가적으로 생겼으므로 제 5 정규화를 통해 다음과 같이 테이블을 분리할 수 있다.