Geometric Transformation

2D Geometric Transformation

기본적인 기하 변환

• 이동 변환(평행 이동) Translation: 행렬 덧셈
  
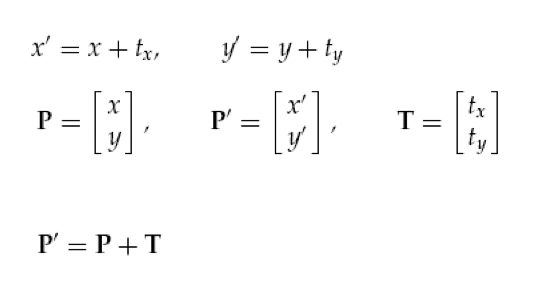
• 회전변환 Rotation: 행렬 곱셈
  
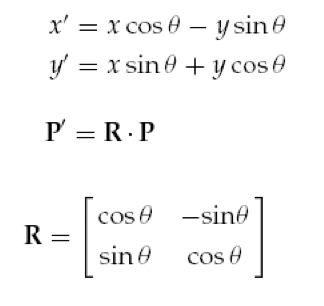
• 사이즈변환 Scaling: 행렬 곱셈
  

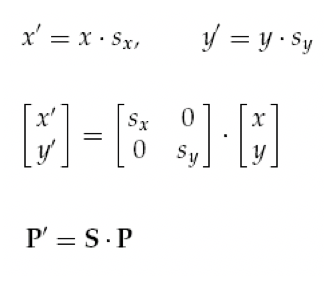
Homogeneous Coordinates

동차 좌표는 2차원 평면 상의 점을 3차원 공간 상의 직선에 사상(mapping) 시킨 것으로 평면에서의 한 점을 2개의 좌표가 아닌 3개의 좌표를 사용하여 표현합니다. 일반적으로 n차원의 사영 공간을 n+1개의 좌표로 나타낸다고 할 수 있습니다. 동차 좌표계는 직교 좌표계에서 0이 아닌 실수 w를 x,y에 곱한 후 마지막에 w로 요소를 하나 더 추가하는 것으로 표현합니다. 점 (x,y)에 대한 동차 좌표 표현은 3차원의 한 직선 상에 무한히 존재합니다. 즉, 한 점으로 변환되지 않는다. 또, 동차 좌표의 마지막 요소(argument) w를 scale factor로 사용하여 벡터와 점을 구별할 수 있습니다. 동차 좌표계에서 0이 아닌 w로 나누어주고 마지막 argument를 제거하면 직교 좌표계를 구할 수 있습니다. 다시 말해, 동차 좌표계를 직교 좌표계로 변환하는 것은 w의 scale과 상관없이 동차 좌표계 위의 한 직선에 있는 모든 점들을 w=1인 평면의 한 점으로 mapping 하는 것입니다.

선형 변환 vs 위치 변환 (affine) vs 투영 변환(perspective/projective):
선형 변환은 오직 스케일링, 회전 등과 같은 변환만 포함합니다. 이동(translation) 변환은 포함하지 않습니다.
위치 변환 (affine 변환)은 선형 변환에 이동(translation) 변환이 추가된 것입니다. 따라서 회전, 스케일링, 그리고 이동을 포함할 수 있습니다.
투영 변환 (perspective/projective 변환)은 3D 공간에서 2D 이미지 표면으로의 투영을 포함합니다. 이는 3D 객체를 2D 화면에 그릴 때 필요한 변환입니다.

동차 좌표의 이점

일반적인 좌표계에서는 위치 변환 및 투영 변환을 단순한 행렬 곱으로 표현하기 어렵습니다. 왜냐하면 이들 변환은 선형적이지 않기 때문입니다. 그러나 동차 좌표계를 도입하면, 이러한 비선형 변환들도 선형 변환처럼 행렬 곱으로 표현할 수 있게 됩니다.
예를 들어, 2D 공간의 점을 이동시키려면 동차 좌표계에서 3x3 행렬을 사용하여 이를 표현할 수 있습니다. 3D 공간의 점을 이동시키려면 4x4 행렬을 사용합니다.
이것은 그래픽스 하드웨어나 알고리즘의 설계에서 큰 이점을 제공합니다. 여러 변환들을 하나의 행렬로 결합하여 연산의 효율성을 크게 향상시킬 수 있기 때문입니다.

그러면 위에서 언급한 기본 변환들은 다음과 같이 변하게 됩니다.

• 이동변환(= 평행이동) Translation: 행렬 곱셈
  
• 회전변환 Rotation: 행렬 곱셈
  
• 사이즈변환 Scaling: 행렬 곱셈
  

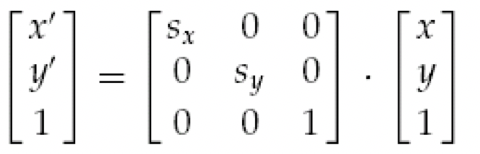
3D나 나머지 변환들은 아래 링크를 참고해주세요. 읽어주셔서 감사합니다!!
기하 변환