.png)
문제
깽미는 24살 모태솔로이다. 깽미는 대마법사가 될 순 없다며 자신의 프로그래밍 능력을 이용하여 미팅 어플리케이션을 만들기로 결심했다. 미팅 앱은 대학생을 타겟으로 만들어졌으며 대학교간의 도로 데이터를 수집하여 만들었다.
이 앱은 사용자들을 위해 사심 경로를 제공한다. 이 경로는 3가지 특징을 가지고 있다.
사심 경로는 사용자들의 사심을 만족시키기 위해 남초 대학교와 여초 대학교들을 연결하는 도로로만 이루어져 있다.
사용자들이 다양한 사람과 미팅할 수 있도록 어떤 대학교에서든 모든 대학교로 이동이 가능한 경로이다.
시간을 낭비하지 않고 미팅할 수 있도록 이 경로의 길이는 최단 거리가 되어야 한다.
만약 도로 데이터가 만약 왼쪽의 그림과 같다면, 오른쪽 그림의 보라색 선과 같이 경로를 구성하면 위의 3가지 조건을 만족하는 경로를 만들 수 있다.
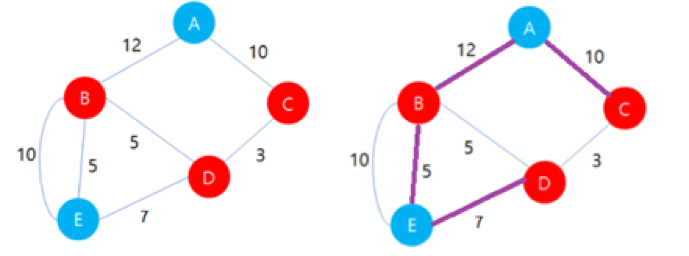
이때, 주어지는 거리 데이터를 이용하여 사심 경로의 길이를 구해보자.
입력
입력의 첫째 줄에 학교의 수 N와 학교를 연결하는 도로의 개수 M이 주어진다. (2 ≤ N ≤ 1,000) (1 ≤ M ≤ 10,000)
둘째 줄에 각 학교가 남초 대학교라면 M, 여초 대학교라면 W이 주어진다.
다음 M개의 줄에 u v d가 주어지며 u학교와 v학교가 연결되어 있으며 이 거리는 d임을 나타낸다. (1 ≤ u, v ≤ N) , (1 ≤ d ≤ 1,000)
출력
깽미가 만든 앱의 경로 길이를 출력한다. (모든 학교를 연결하는 경로가 없을 경우 -1을 출력한다.)
풀이
최소 스패닝 트리(MST)를 구하는 알고리즘에서 유니온파인드를 이용한 크루스칼 알고리즘을 이용하여 푸는 문제이다.
이 문제를 풀기에 앞서 유니온 파인드의 개념을 잘 숙지하는 것이 중요하다.
크루스칼은 간선을 가중치를 기준으로 오름차순 정렬되어있는 우선순위 큐를 이용하여 구한다.
그 다음 우선순위 큐를 하나씩 꺼내면서 find 함수로 구해진 두 정점의 부모노드가 같지 않다면 Union 해주는 방식을 이용한다.
이 크루스칼 알고리즘을 이용한다면 최소 거리로만 이루어진 최소 신장 트리가 완성이 될 것이다.
이 문제는 무조건 남자와 여자와 이어지는 간선만 최소 스패닝 트리에 들어가므로 주어진 입력값을 처리할 때 이어지는 간선이 동성일 경우는 제외하고 구해야한다.
Source Code
package 최소스패닝트리.`14621번_나만_안되는_연애`
import java.util.*
private lateinit var parents : Array<Int>
fun main(args : Array<String>) = with(System.`in`.bufferedReader()) {
val (N, M) = readLine().split(" ").map { it.toInt() }
val gender = readLine().split(" ")
val pq = PriorityQueue<Node>()
parents = Array(N + 1) {i -> i}
for(i in 0 until M) {
val (start, end, weight) = readLine().split(" ").map {it.toInt()}
/** 서로 성별이 다른 사람끼리만 연결 **/
if (gender[start - 1] == gender[end - 1]) continue
pq.offer(Node(start, end, weight))
}
var cnt = 0
var ans = 0
while (!pq.isEmpty()) {
val cur = pq.poll()
val a = find(cur.start)
val b = find(cur.end)
if (a == b) continue
union(a, b)
ans += cur.weight
if (++cnt == N - 1) break
}
println(if (cnt < N - 1) {-1} else {ans})
}
fun union(a : Int, b : Int) {
val A = find(a)
val B = find(b)
if (A == B) return
parents[B] = A
}
fun find(x : Int) : Int{
if (parents[x] == x) return x
parents[x] = find(parents[x])
return parents[x]
}
data class Node(val start : Int, val end : Int, val weight : Int) : Comparable<Node> {
override fun compareTo(o : Node) = weight - o.weight
}