[프로그래머스] 거스름돈 (C++)

문제

https://school.programmers.co.kr/learn/courses/30/lessons/12907

아이디어1

동적 계획법(Dynamic Programming)

• 점화식 구하기

• case(i, n) :
  money[0] ~ money[i]의 동전으로 n 원을 거슬러 주는 방법의 수
• 그러면 money[i] 동전이 0개일 때, 1개일 때, ...
  money[0] ~ money[i - 1]의 동전으로 n 원을 거슬러 주는 방법의 수 들의 합과 같음
• 점화식으로 쓰면
  $case(i, n) = case(i - 1, n) + case(i - 1, n - money[i]) + case(i - 1, n - 2 * money[i]) + ...$
• 이 때
  $case(i - 1, n - money[i]) + case(i - 1, n - 2 * money[i]) + ...$
  는
  $case(i, n - money[i])$
  와 같음
• 즉,
  $case(i, n) = case(i - 1, n) + case(i, n - money[i])$
  이 됨
  
  
• i와 n을 각각 행과 열이 되는 dp 행렬을 만들면 됨

vector<vector<int>> dp(money.size(), vector<int>(n + 1,0));
for (int i = 0; i < dp.size(); ++i)
{
    for (int j = 0; j <= n; ++j)
    {
        if (i - 1 < 0)
        {
            if (j % money[i] == 0)
                dp[i][j] = 1;
        }
        else if(j < money[i])
        {
            dp[i][j] = dp[i - 1][j];
        }
        else
            dp[i][j] = dp[i - 1][j] + dp[i][j - money[i]];
    }
}

• i = 0 일 때,
  money[0] 동전만으로 거스름돈을 줄 수 있으면 1
  아니면 0
• 거스름돈이 0원인 경우는 없지만 1이라고 해둠
  • 거스름돈이 2원일 때 2원 동전으로 제출할 수 있는 방법 1가지가 있기 때문에 더하기 위한 값

<테스트 케이스>

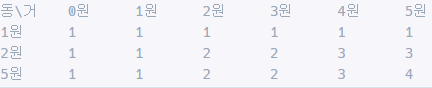
• 1, 2, 5원으로 거스름돈 5원은 4가지