[알고리즘] KMP

프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략을 보면서 정리한 내용입니다.

문자열 검색 문제

문자열 N이 문자열 H의 일부인지 확인하기 하고, 일치한다면 그 H에서의 시작 위치를 담는 문제를 문자열 검색 문제라고 한다.

예를 들어 H = "ABCDE", N = "BCD"이면 H[1:4]가 N이 되므로 H는 N을 포함한다.

단순한 문자열 검색

이를 풀기 위해 가장 간단한 방법은 N의 가능한 모든 시작 위치를 확인해 보는 것이다.

코드

def easy_search(H,N):
    result = []
    for h_idx in range(len(H)):
        checked = 1
        for n_idx in range(len(N)):
            if H[h_idx + n_idx] == N[n_idx]:
                continue     
            checked = 0
            break
        
        if checked:
            result.append(h_idx)
    return result
r =easy_search("ABCDE","BCD")
print(r)

단점

위 코드는 문자열의 모든 문자에 대해 비교해, 시간복잡도가 O(len(N)*len(M))이다. 문자열의 길이가 길다면 비효율적이다.

KMP 알고리즘

그래서 나온게 KMP 알고리즘이다. 위의 단순 비교에서는 버려지는 정보가 존재한다. H[i] == N[j]에서 틀렸다면 위 코드에서는 H[i+1]를 N[0]부터 다시 비교하지만 N[j - 1]까지는 맞았다는 정보를 재사용하면 시간복잡도를 줄일 수 있다.

얻어낸 정보

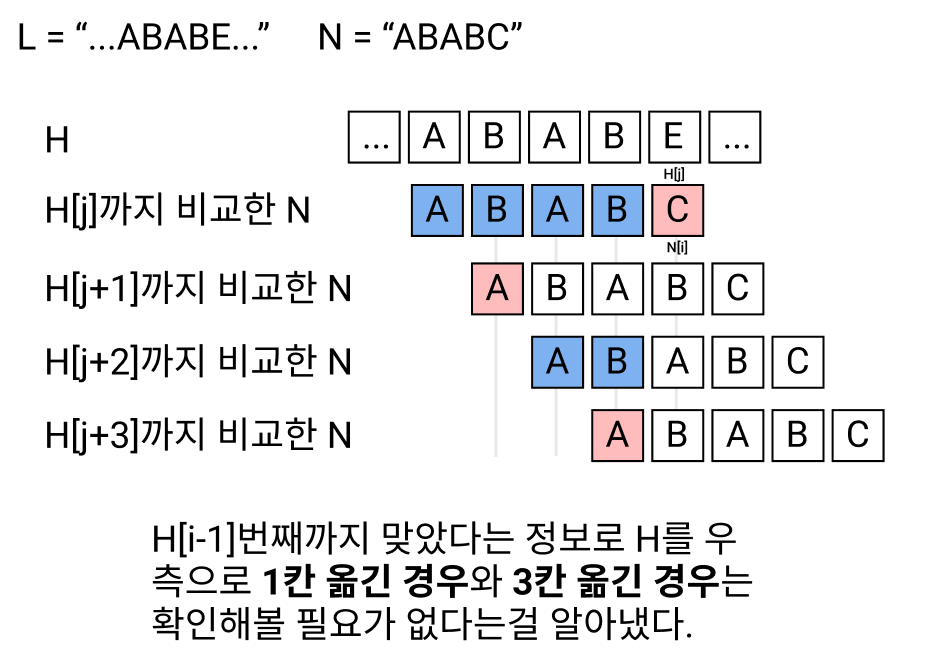
이 정보를 이용해서 바로 2칸 옮긴 경우부터 탐색을 하면 된다.

그렇다면

몇번째에서 틀렸는지를 가지고 다음에 탐색해야할 경우를 찾아놓는다면 빠르게 문자열 비교를 수행할 수 있다. 이 개념을 적용한 문자열 검색 알고리즘이 KMP 알고리즘이다.

부분 일치 테이블

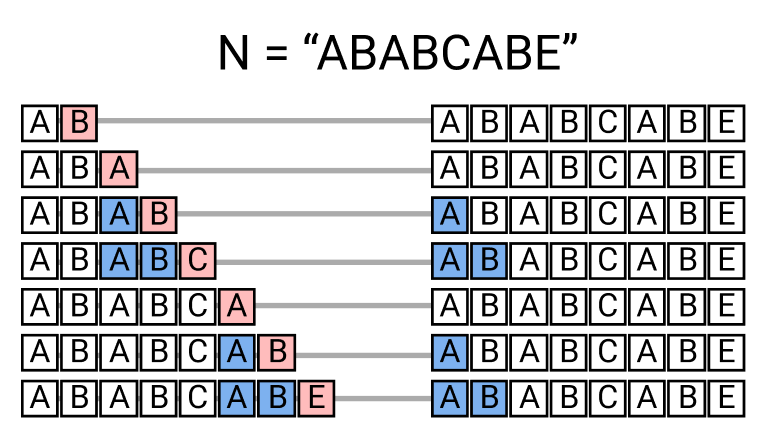
• N이 i 번째까지 맞았을 경우 탐색을 시작할 다음 위치

i	탐색을 재개할 N의 다음 위치
0	0
1	0
2	1
3	2
4	0
5	1
6	2
7	0

i번째까지 일치했을 때 다음 시작할 위치를 담고 있는 이 테이블을 부분 일치 테이블이라고 한다. (일치가 실패했을 때 어떻게 해야하는지 말해준다는 의미에서 실패 함수라고 부르기도 한다.)

다음 시작 위치가 되기 위해서는 N[:i+1]까지의 시작 부분과 끝 부분이 일치해야햔다. 즉 접두사와 접미사가 같을 때의 최대 길이가 된다.

부분 일치 테이블을 pi라고 두면,

pi[i] = N[:i+1]의 접두사이자 접미사인 문자열의 최대 길이

로 정의할 수 있다. 그렇다면 이 부분 일치 테이블은 어떻게 만들까?

단순한 코드

def get_partial_match(N):
    M = len(N)
    pi = [0] * M
    for begin in range(1,M):
        for f_len in range(M - begin):
            if N[begin + f_len] != N[f_len]: # begin + f_len == i
                break
            pi[begin + f_len] = max(pi[begin + f_len], f_len+ 1)
    return pi

단순히 모든 경우에 대해 비교함으로써 부분 일치 테이블을 만들 수 있다. N이 짧은 경우에는 상관 없지만 N이 길 경우에는 시간 복잡도가 O(N^2)이기에 비효율 적이다.

추후 최적화를 적용하자.

KMP 알고리즘을 이용한 문자열 검색

코드

# H에서 N이 존재하는 시작 위치 모두 리턴
def kmp_search(H,N):
    J = len(H)
    M = len(N)
    # 부분 일치 테이블
    pi = get_partial_match(N)
    result = []

    begin = 0
    matched = 0
    # H의 시작 위치가 J-M을 넘어가면 일치하는건 존재X
    while begin < J -M:
        # 같다면 matched의 길이 증가
        if matched < M and H[begin + matched] == N[matched]:
            matched += 1
            if(matched == M):
                result.append(begin)
        # matched가 0이라면 pi를 이용해 갱신 X
        elif matched == 0:
            begin += 1
        # begin + matched에서 일치에 실패했다면
        # begin(시작 위치)를 다음 시작 위치로 만들기
        # pi[matched - 1] == (matched - 1)만큼 일치할 때
        # 다음 시작 위치는 matched - pi[matched - 1]이 된다.
        # 다음 matched가 pi[matched -1] 되야하기 때문
        else:
            begin += matched - pi[matched - 1]
            matched = pi[matched - 1]
    return result

이 알고리즘은 항상 begin이나 matched가 1씩 증가하므로 총 len(H) - len(N)번 수행된다. 그리고 부분 일치 테이블을 만드는데에 len(N)^2의 시간이 걸리므로 그러므로 시간 복잡도는 O(len(H) + len(N)^2)이다.

부분 일치 테이블을 만드는데 시간이 너무 오래 걸리는데, KMP 알고리즘을 적용해 빠르게 개선이 가능하다. 접두사와 접미사가 같은 문자열의 최대 길이를 찾으면 된다. 즉 찾는 문자열 N 스스로에 대해서 KMP 알고리즘을 적용하면 된다.

KMP를 적용한 부분 일치 테이블 생성 코드

def better_get_partial_match(N):
    M = len(N)
    pi = [0] * M
    
    begin = 1
    matched = 0
    while begin + matched < M:
        if N[begin + matched] == N[matched]:
            matched += 1
            # matched가 증가할때 이전의 값 갱신해줌
            # 0일 경우에는 default이기에 갱신 X
            pi[begin + matched - 1] = matched
        elif matched == 0: 
            begin += 1
        else:
            # 루프가 한번 더 돌면서 얘네에 대해서 
            # 매칭 되는지 검증하고 pi를 갱신하니까
            # 여기서는 pi값 갱신 X
            begin += matched - pi[matched - 1]
            matched = pi[matched - 1]
    return pi

최적화된 부분 일치 테이블 생성의 시간 복잡도는 O(len(N))이다.
부분 일치 테이블 생성마저 최적화한다면 KMP 알고리즘을 이용한 문자열 검색의 최종적인 시간 복잡도는 O(len(H) + len(N))이다.

최종 코드

def better_get_partial_match(N):
    M = len(N)
    pi = [0] * M
    
    begin = 1
    matched = 0
    while begin + matched < M:
        if N[begin + matched] == N[matched]:
            matched += 1
            pi[begin + matched - 1] = matched
        elif matched == 0: 
            begin += 1
        else:
            begin += matched - pi[matched - 1]
            matched = pi[matched - 1]
    return pi

def kmp_search(H,N):
    J = len(H)
    M = len(N)
    pi = better_get_partial_match(N)
    result = []

    begin = 0
    matched = 0
    while begin < J - M:
        if matched < M and H[begin + matched] == N[matched]:
            matched += 1
            if(matched == M):
                result.append(begin)
        elif matched == 0:
            begin += 1
        else:
            begin += matched - pi[matched - 1]
            matched = pi[matched - 1]
    return result

코멘트

KMP는 배워도 배워도 자꾸 까먹는다. 얄궂다 정말.

틀린점이 있다면 꼭 지적해주세요. 제가 잘 모르고 있을 확률 99%.