LV2_가장 큰 정사각형 찾기(C++)

🚗문제 설명

1와 0로 채워진 표(board)가 있습니다. 표 1칸은 1 x 1 의 정사각형으로 이루어져 있습니다. 표에서 1로 이루어진 가장 큰 정사각형을 찾아 넓이를 return 하는 solution 함수를 완성해 주세요. (단, 정사각형이란 축에 평행한 정사각형을 말합니다.)

예를 들어

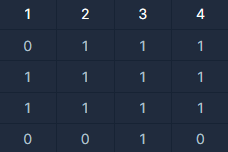
가 있다면 가장 큰 정사각형은

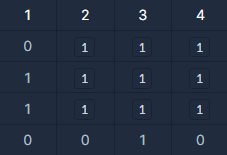
가 되며 넓이는 9가 되므로 9를 반환해 주면 됩니다.

🚓제한 조건

표(board)는 2차원 배열로 주어집니다.
표(board)의 행(row)의 크기 : 1,000 이하의 자연수
표(board)의 열(column)의 크기 : 1,000 이하의 자연수
표(board)의 값은 1또는 0으로만 이루어져 있습니다.

🚕입출력 예시

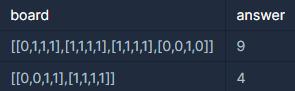
🚕입출력 설명

입출력 예 #1
위의 예시와 같습니다.

입출력 예 #2
| 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
로 가장 큰 정사각형의 넓이는 4가 되므로 4를 return합니다.

🚐코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int solution(vector<vector<int>> board){
    
    //int answer = 0;으로 하면 오류 발생
    //board[i][0] = 1, board[0][i] = 1 이고 나머지가
    //0으로 채워져 있을 때 가장 큰 정사각형이 1이 되도록 한다.
    int answer = board[0][0];
    
    int i, j;
    for(i=1;i<board.size();i++){
        for(j=1;j<board[0].size();j++){
            if(board[i][j] == 1){
                board[i][j] = min(board[i-1][j], board[i][j-1]);
                board[i][j] = min(board[i][j], board[i-1][j-1]) + 1;
                answer = max(answer, board[i][j]);
            }
        }
    }

    return answer*answer;
}

🚀+) DP(Dynamic Programming, 동적 계획법)

직관적으로 가면서 3중 for문을 사용하는 문제는 아닌 것 같았다. 그래서 자료를 찾아보니까 DP라는 개념이 있었다.

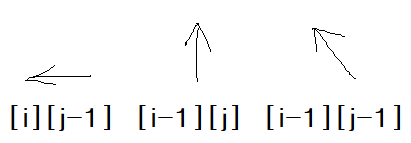
1) TOP-DOWN

큰 문제를 해결하려고 작은 문제를 호출하는 방식이다. 점화식을 통해 이해하기 쉽다는 장점을 갖고 있다.

int memo[100];
public int fibonacci(int n) {
    if (n <= 1)
        return n;
    else if (n == 2)
        return 1;
    else {
        if (memo[n] > 0)
            return memo[n];
        memo[n] = fibonacci(n-1) + fibonacci(n-2);
        return memo[n];
    }
}

2) BOTTOM-UP

가장 작은 문제부터 답을 구하며 큰 문제의 답을 찾는 방식이다. 재귀 호출을 하지 않아 메모리 사용량 감소를 기대할 수 있다.

int d[100];
public int fibonacci(int n) {
    d[0] = 0;
    d[1] = 1;
    for (int i = 2; i <= n; i++) {
        d[i] = d[i - 1] + d[i - 2];
    }
    return d[n];
}

---

DP를 활용하는 것에 익숙해져야 할 것 같다.