Day 41

Machine Learning Day 16

* Decision Tree - is used for distinguishing Feature Importance
* KNN Clustering - is used for pre-training of YOLO(You Only Look Once) Algorithm
* Bayesian Inference - relationship between Prior Probability and Posterior Probability

=> These things matter for understanding the concept of what Algorithm is.

• Bayesian Inference = a step for better understanding of Gausian Algorithm

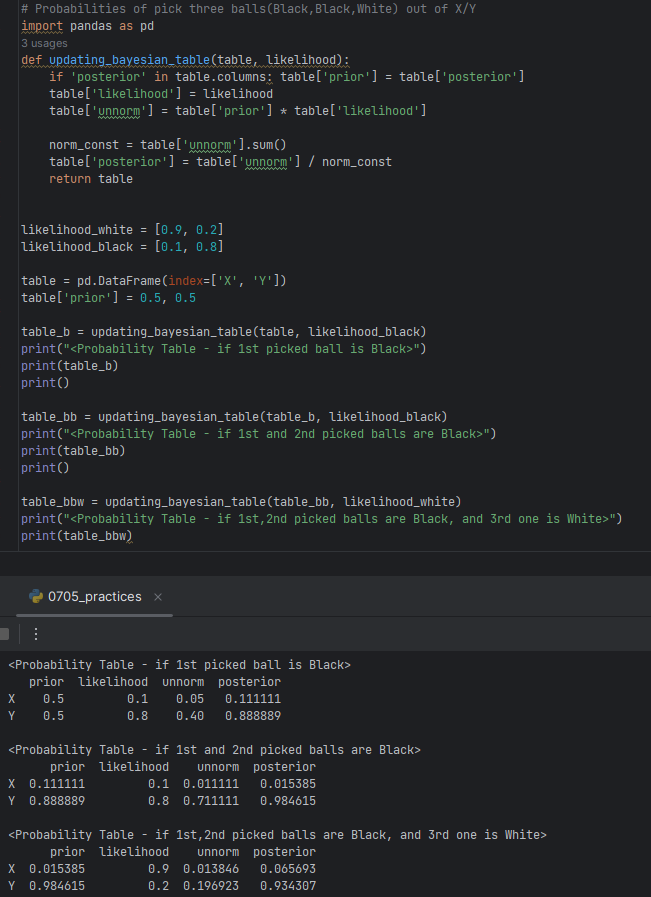
<Exercise.1>

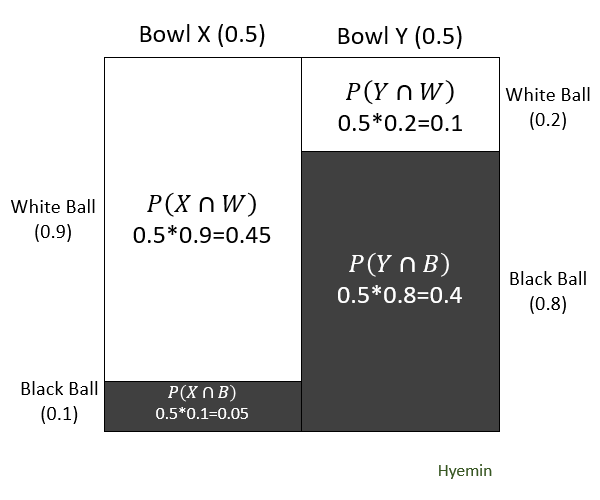
• Posterior Probabilities
  $P(X|W) \;=\; \frac{P(X)\cdot P(W|P)}{P(W)} \;=\; \frac{P(X\cap W)}{P(X\cap W)+P(Y\cap W)} \;=\; \frac{P(X)\cdot P(W|X)}{P(X)\cdot P(W|X)+P(Y)\cdot P(W|Y)}$
  $P(X|B) \;=\; \frac{P(X)\cdot P(B|X)}{P(B)} \;=\; \frac{P(X\cap B)}{P(X\cap B)+P(Y\cap B)} \;=\; \frac{P(X)\cdot P(B|X)}{P(X)\cdot P(B|X)+P(Y)\cdot P(B|Y)}$
  $P(Y|W) \;=\; \frac{P(Y)\cdot P(W|Y)}{P(W)} \;=\; \frac{P(Y\cap W)}{P(X\cap W)+P(Y\cap W)} \;=\; \frac{P(Y)\cdot P(W|Y)}{P(X)\cdot P(W|X)+P(Y)\cdot P(W|Y)}$
  $P(Y|B) \;=\; \frac{P(Y)\cdot P(B|Y)}{P(B)} \;=\; \frac{P(Y\cap B)}{P(X\cap B)+P(Y\cap B)} \;=\; \frac{P(Y)\cdot P(B|Y)}{P(X)\cdot P(B|X)+P(Y)\cdot P(B|Y)}$

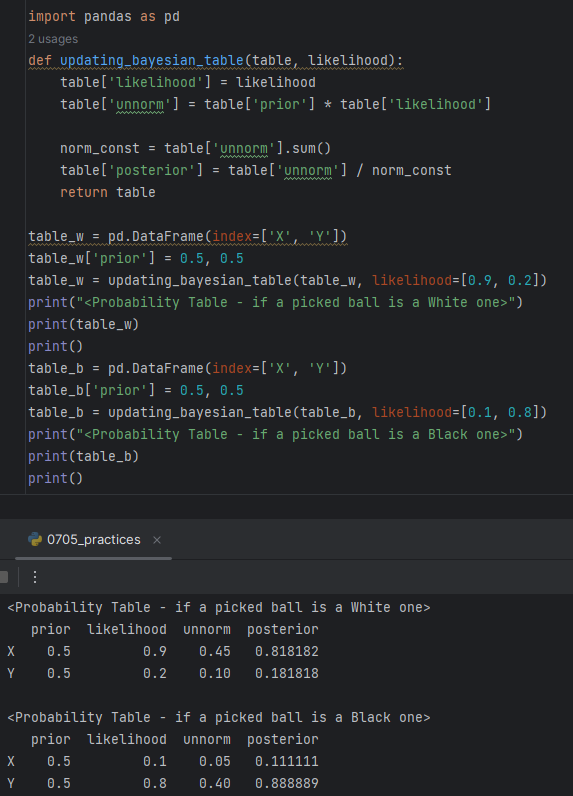
<Exercise.2>

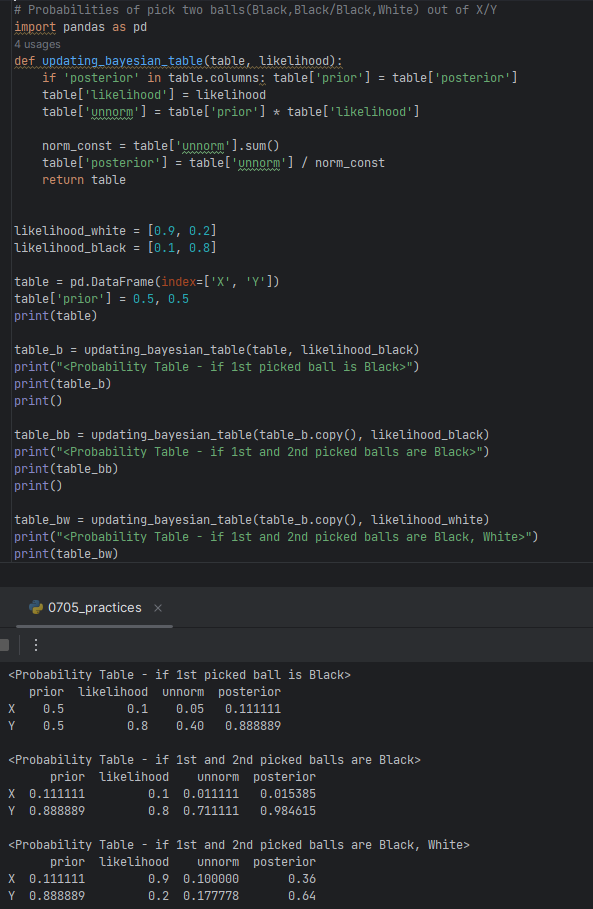
<Exercise.3>

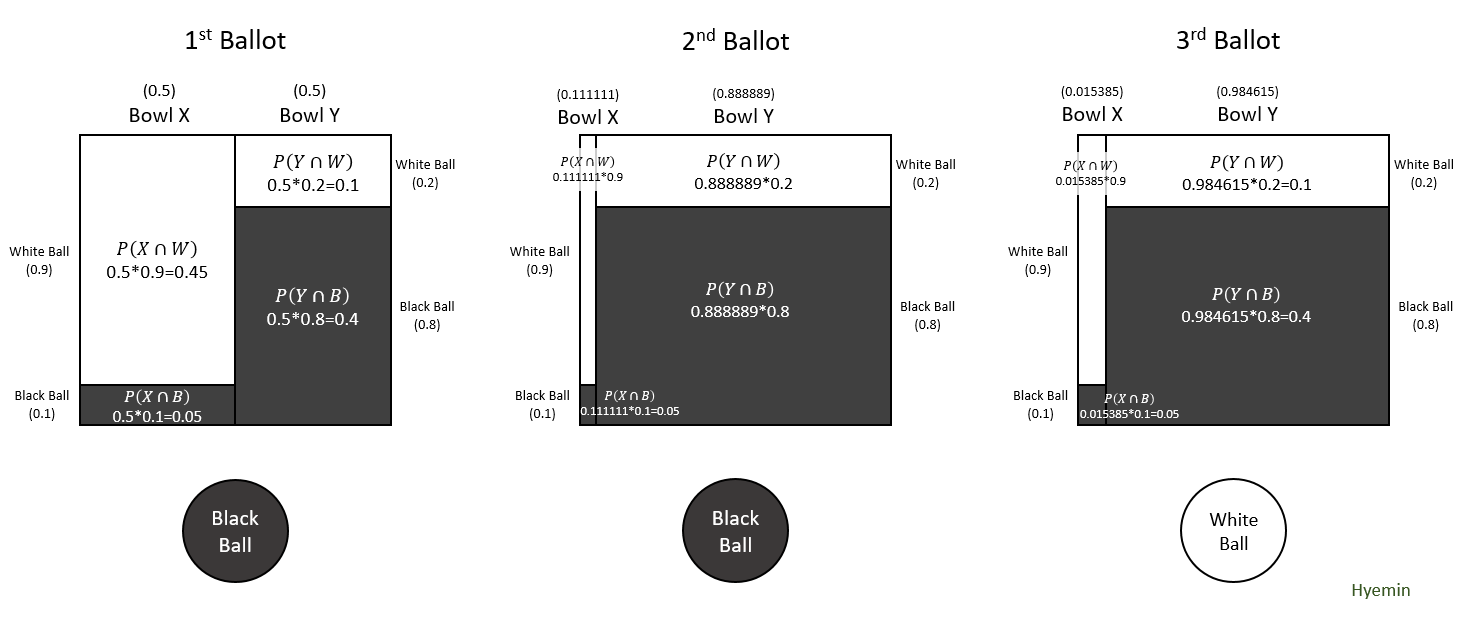
• Naive Bayes: Bayes Inference just assumes that A and B are Independent even though the two have some degree of dependence.
  e.g) "Investment" and "Return-Rate" can be dependent within a context although they are the two very different words.