[백준/C++] 1405. 미친로봇

1405 미친로봇

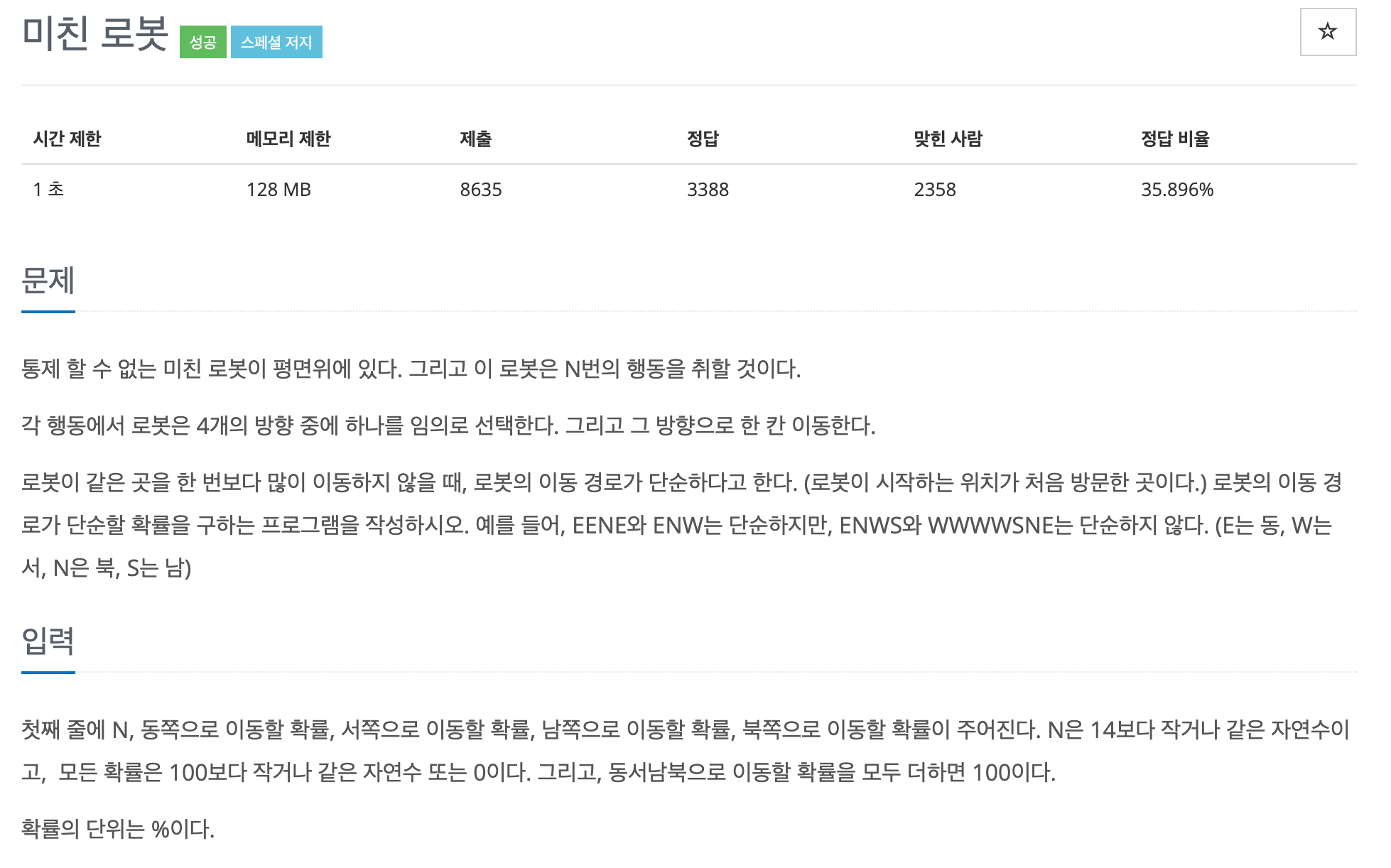
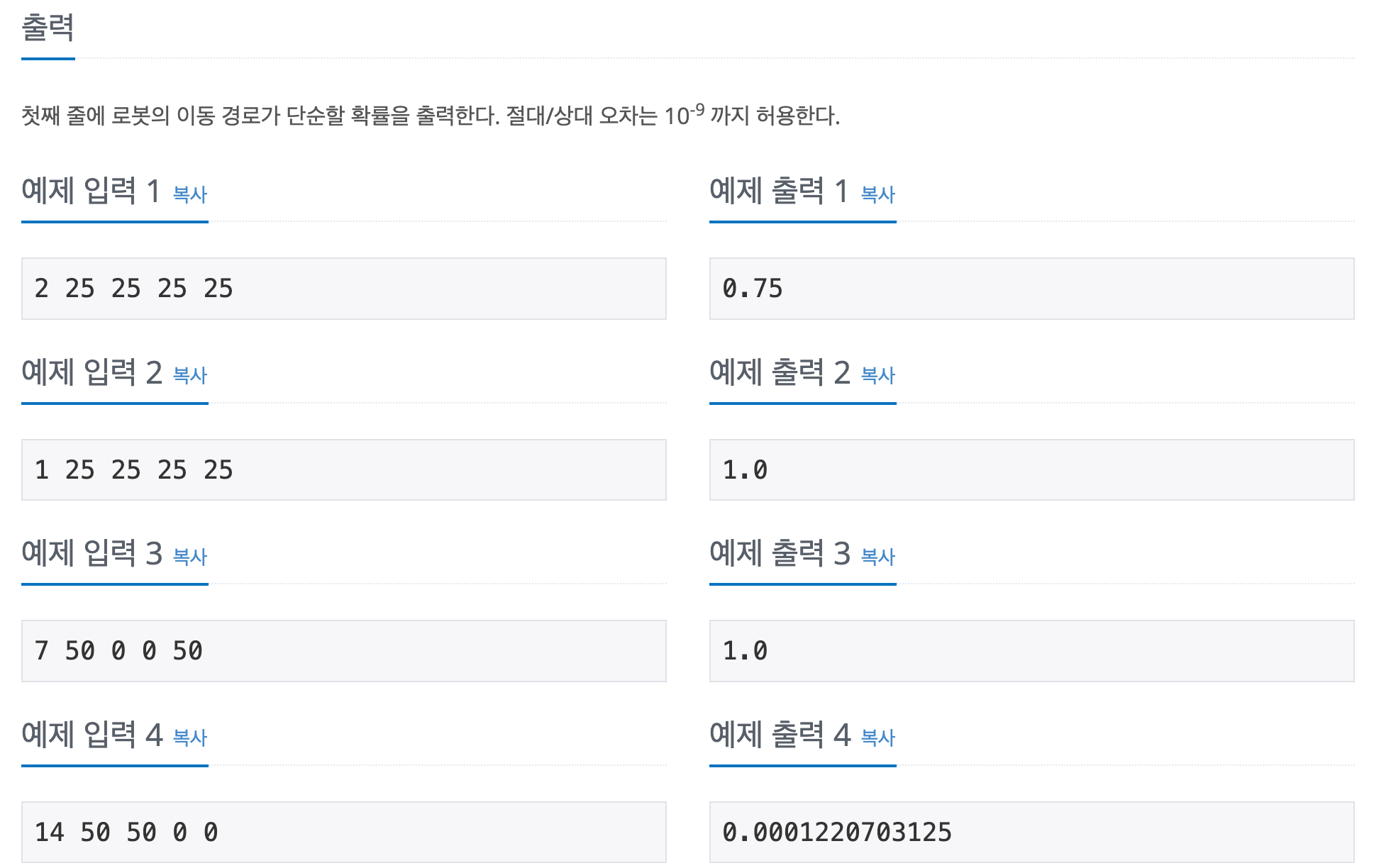
한 번 행동에 동서남북으로 각 한 칸씩 이동하는 로봇이 있는데 N번 움직인다고 하자. 동서남북으로 이동할 확률을 입력하여 단순한 경로를 이동할 확률을 알아보자! 첨엔 이해가 잘 안됐는데 그럴 땐 그림을 그려보면 된다!

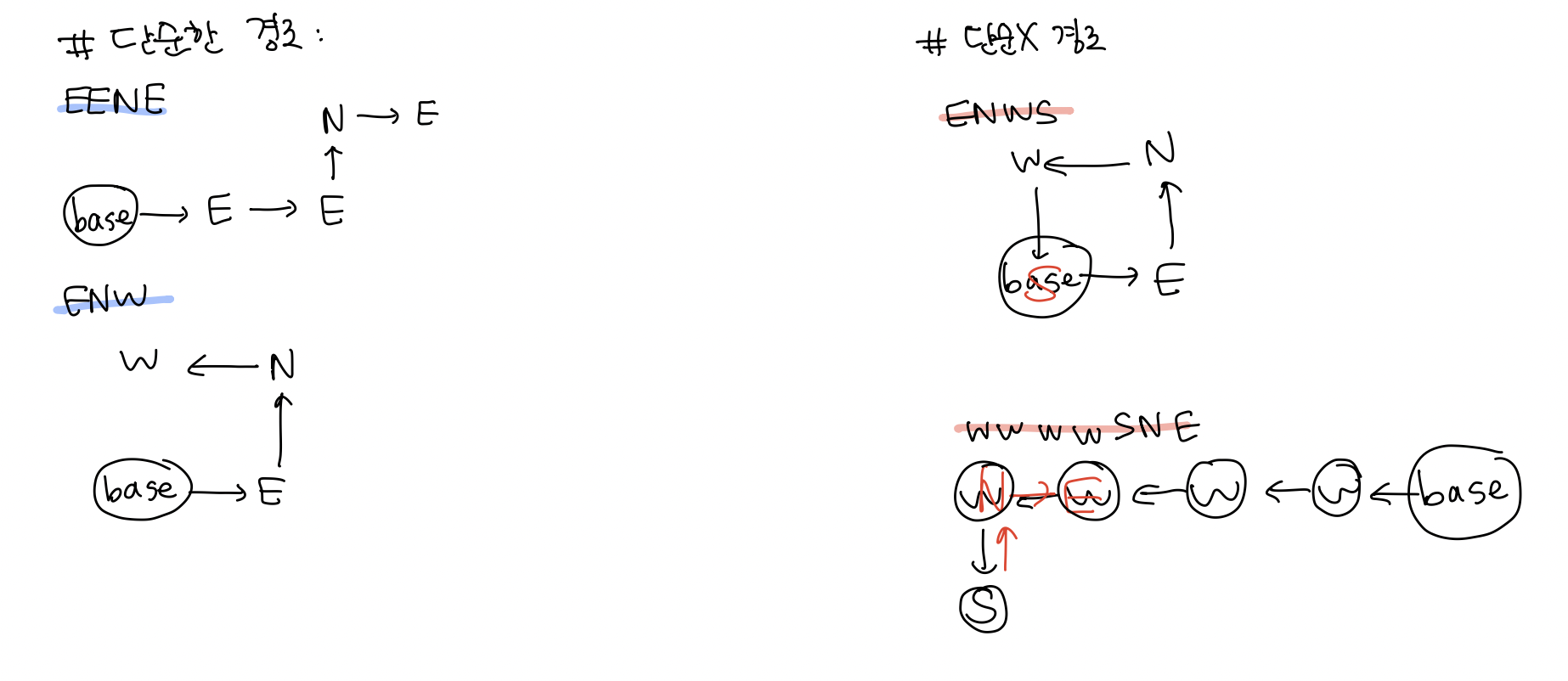단순한 경로는 다음처럼 갔던 곳을 다시 가지 않는 경우이다. 어쩌면 그래프보다는 E-W, N-S 를 카운트해보는 것도 좋을 것 같다.

어쨋든 이것을 그래프로 생각하면 깊이우선탐색으로 각각 경로를 찾아서 확률을 누적합으로 구하고 한 번 다 돌았으면 모두 초기화해서 경로를 탐색하는 방법으로 하면 좋을 것 같다.

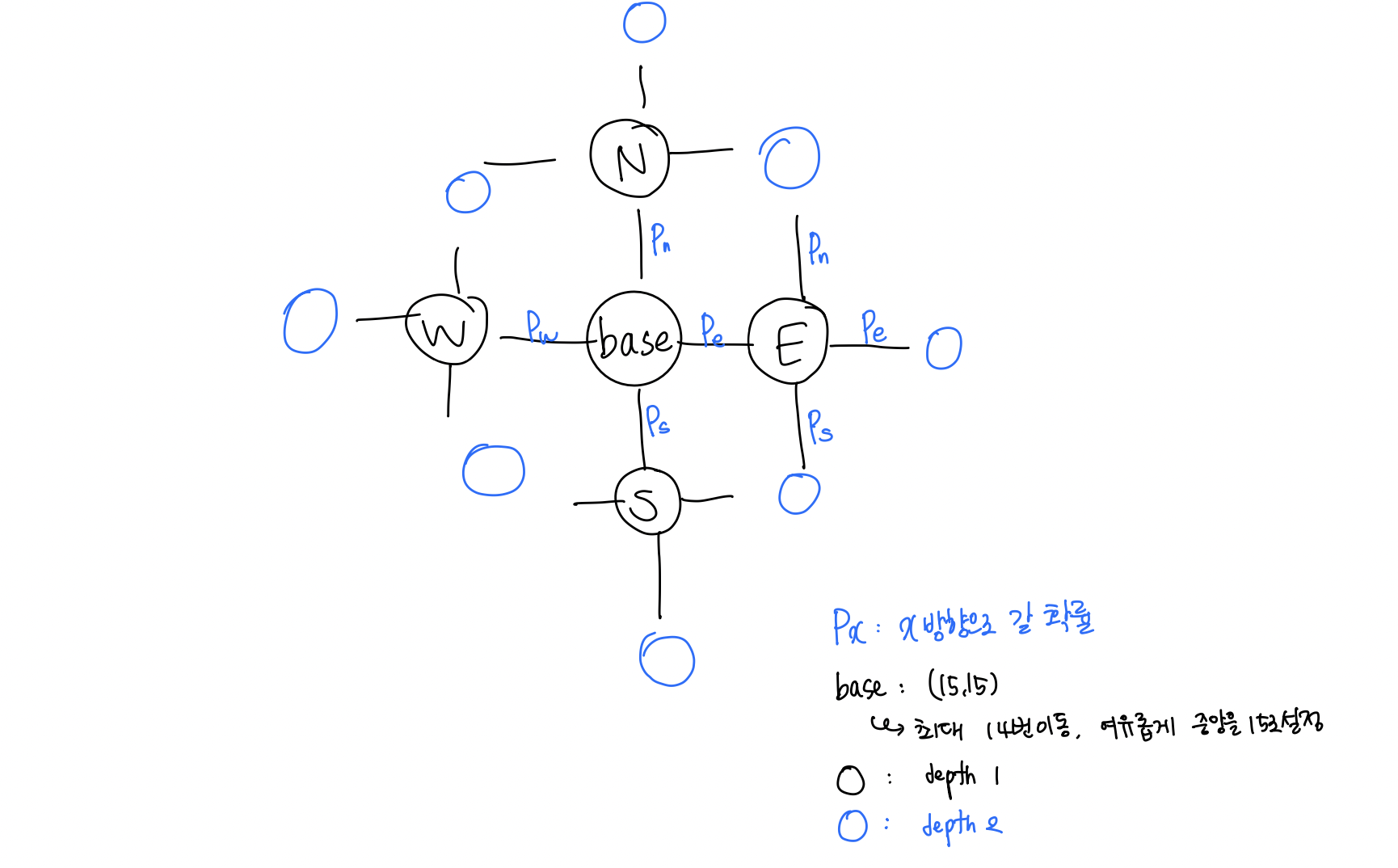그림에서의 depth를 코드로는 변수 d 로 설정해주었고, 이동 횟수를 n으로 받았을 때 d는 n보다 작아야하며 같으면 그것이 종료 조건이 된다.
개발자는 코드로 말하는 거니까(from 굣님) 코드로 봅시다

#include <iostream>
#include <algorithm>
using namespace std;

bool visited[30][30] = {false, };
double prob[4];
int prow[4] = { 1, -1, 0, 0 };
int pcol[4] = { 0, 0, 1, -1 };
int n;
double ans = 0.0;

double dfs(int x, int y, int d){

    if(d == n){
        return 1.0;
    }

    double ans_prob = 0.0;

    visited[x][y] = true;

    for(int i = 0; i<4; i++){
        int nx = x + prow[i];
        int ny = y + pcol[i];
        
        if(!visited[nx][ny]){
            ans_prob += prob[i] * dfs(nx, ny, d+1);
        }
    }
    visited[x][y] = false;
    return ans_prob;
}


int main(void){
    cin>>n;
    for(int i = 0; i<4; i++){
        int num;
        cin>>num;
        prob[i] = num/100.0;
    }

    ans = dfs(15, 15, 0);
    cout.precision(10);
    cout<<fixed<<ans<<endl;

    return 0;
}

dfs 리턴 전에 false로 바꿔주어야지 안그러면 이미 간 곳이라고 생각하고 다른 경로를 탐색할 때 가지 않는다...이걸로 1시간 헤맴
그럼 내일도 화이팅