[백준/C++] 14938. 서강그라운드

Floyd Warshall Algorithm
플로이드 와샬 알고리즘은 모든 정점에서 모든 정점으로의 최단 경로를 탐색하는 알고리즘입니다. 3중 for문을 사용하는 것이 특징이며 중간의 노드를 기준으로 최단 거리를 구한다. 관련된 예제인 백준 14938 서강그라운드 문제를 풀어보도록 하자!

서강그라운드

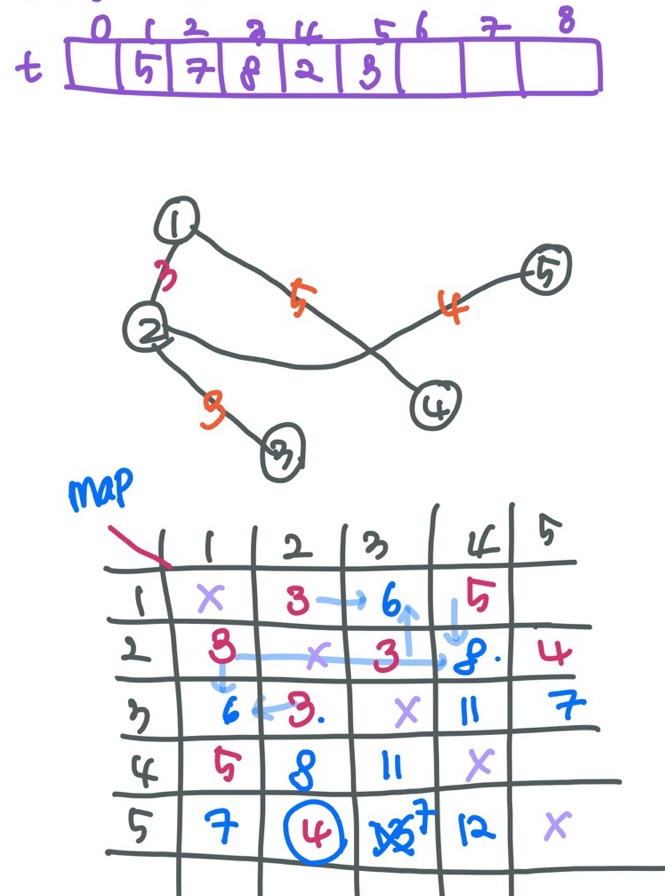
각 정점에서 얻을 수 있는 아이템 개수에 대한 배열은 따로 만들어두고, 플로이드 와샬 알고리즘을 이용해 각 정점에 대한 최단 수색 거리를 구합니다. 그 다음, 모든 노드에서 시작하여 최대로 모을 수 있는 아이템의 수를 비교해서 출력해줍니다. 예제입력 1에 대한 배열은 다음 그림과 같습니다.

조심해야할 점은 착지하는 정점의 아이템도 먹어야하기 때문에 i=j 인 배열을 0으로 초기화해주어서 맨 아래 for문에서 착지지점 아이템도 셀 수 있도록 해주어야합니다!

#include <iostream>
#include <algorithm>
#define MAX 12345;
using namespace std;

int n, m, r;
int t[101] = {0, };
int map[101][101] = {0, };

int main(){
    cin>>n>>m>>r;

    for(int i = 0; i<101; i++){
        for(int j = 0; j<101; j++){
            if(i!=j){
                map[i][j] = MAX;
            }
        }
    }
    
    for(int i = 1; i<=n; i++){
        cin>>t[i];
    }

    for(int i = 0; i<r; i++){
        int a, b, l;
        cin>>a>>b>>l;
        map[a][b] = l;
        map[b][a] = l;
    }

    for(int k = 1; k<=n; k++){
        for(int i = 1; i<= n; i++){
            for(int j = 1; j<=n; j++){
                if(map[i][j] > map[i][k] + map[k][j]){
                    map[i][j] = map[i][k] + map[k][j];
                }
            }
        }
    }
    int max_item = 0;
    for(int i = 1; i<=n; i++){
        int temp = 0;
        for(int j = 1; j<=n; j++){
            if(map[i][j]<= m){
                temp = temp + t[j];
            }
        }
        max_item = max(max_item, temp);

    }
    cout<<max_item;
}

그럼 오늘도 화이팅><