문제

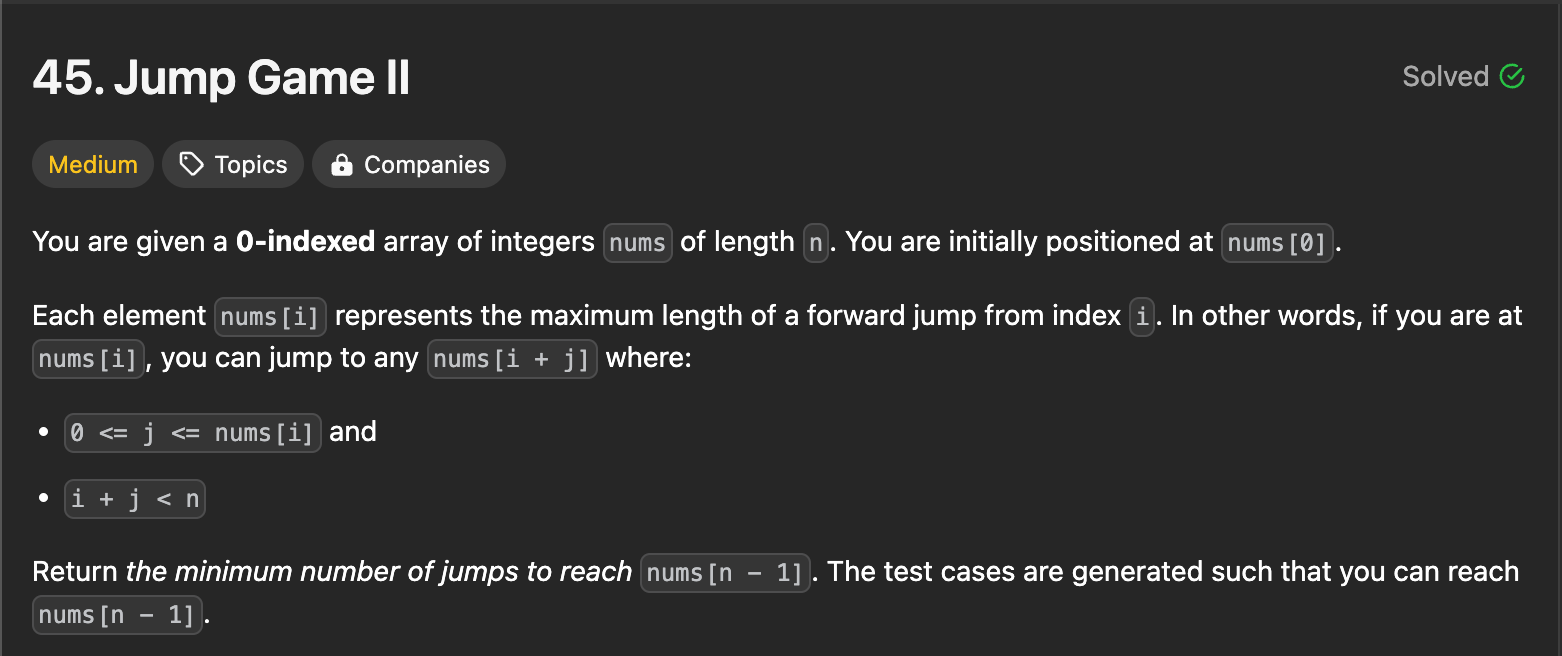
한국어 번역

당신에게는 길이 n의 정수들로 이루어진 0-인덱스 배열이 주어진다. 당신은 처음에 nums[0]에 위치한다.

각 원소 nums[i]는 인덱스 i에서 앞으로 점프하는 최대 길이를 나타낸다. 즉, nums[i]에 있으면 0 < = j < = nums [ i ] 및 i + j < n 를 만족하는 j에 대해 nums[i + j]로 점프할 수 있다.

num[n - 1]에 도달할 수 있는 최소 점프 횟수를 반환하라. 테스트 케이스는 num[n - 1]에 도달할 수 있도록 생성된다.

제약조건

• 1 <= nums.length <= 10^4
• 0 <= nums[i] <= 1000
• nums[n - 1]에 무조건 도달할 수 있다.

문제 접근

나는 처음에 이 문제를 보고 무조건 Dynamic Programming으로 해결해야겠다고 생각했다. 최대로 점프할 수 있는 idx를 저장하는 dp라는 vector를 생성해 모든 index를 차례로 방문하면서 dp[nums.size()-1] 를 반환하면 되기 때문이다.
따라서 나는 다음과 같이 코드를 작성했다.

내 코드

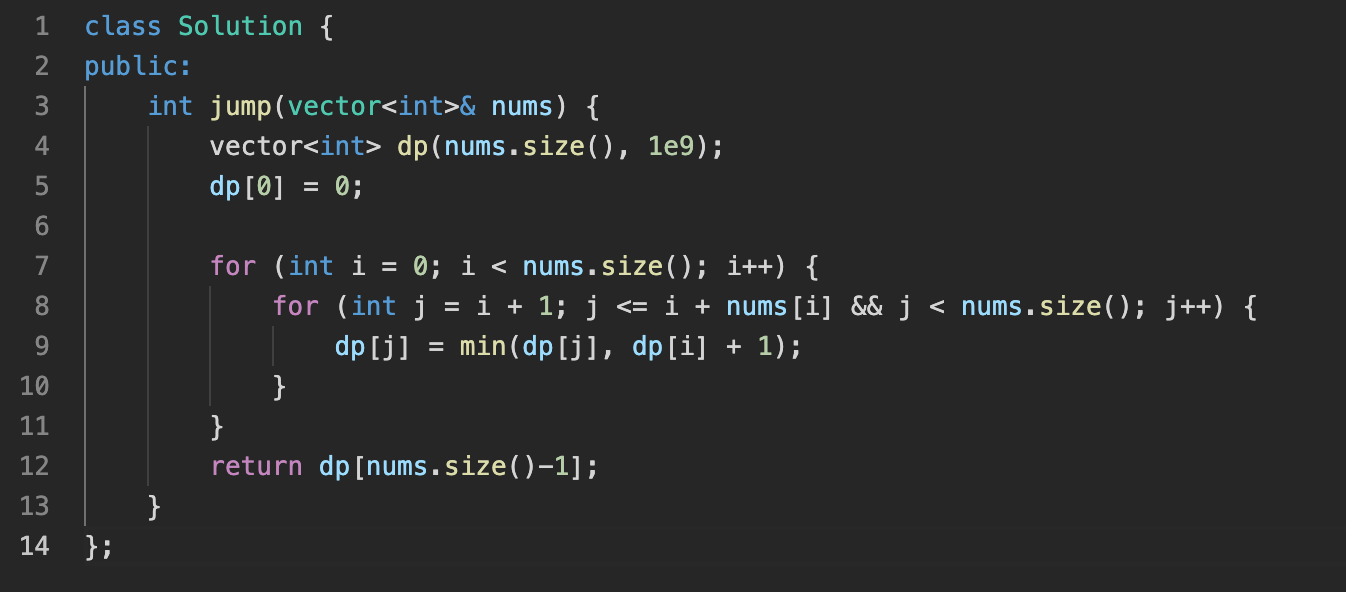
결과

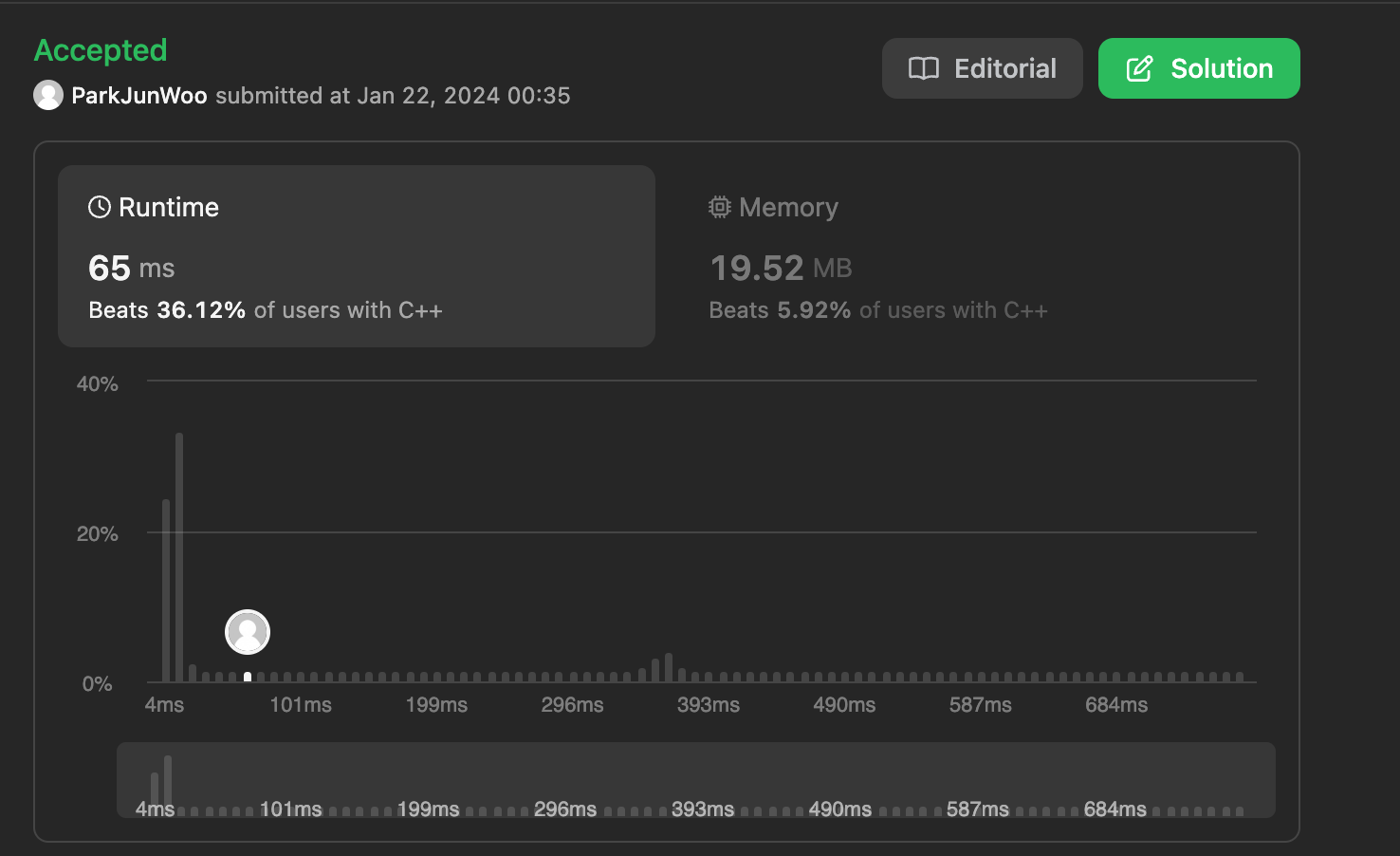
정답은 맞는데... 실행시간과 메모리의 관점에서 너무 비효율적인 코드인 것 같다...
그래서 가장 빠른 실행시간을 가진 사람들의 코드를 참고해 다시 작성해보았다.

Prefix를 활용한 효율적인 저장

나처럼 모든 idx를 탐색하며 점프할 수 있는 모든 idx를 도는 것은 비효율적이다. 왜 그런지 예시를 통해 살펴보자.

DP를 사용한 풀이 효율성

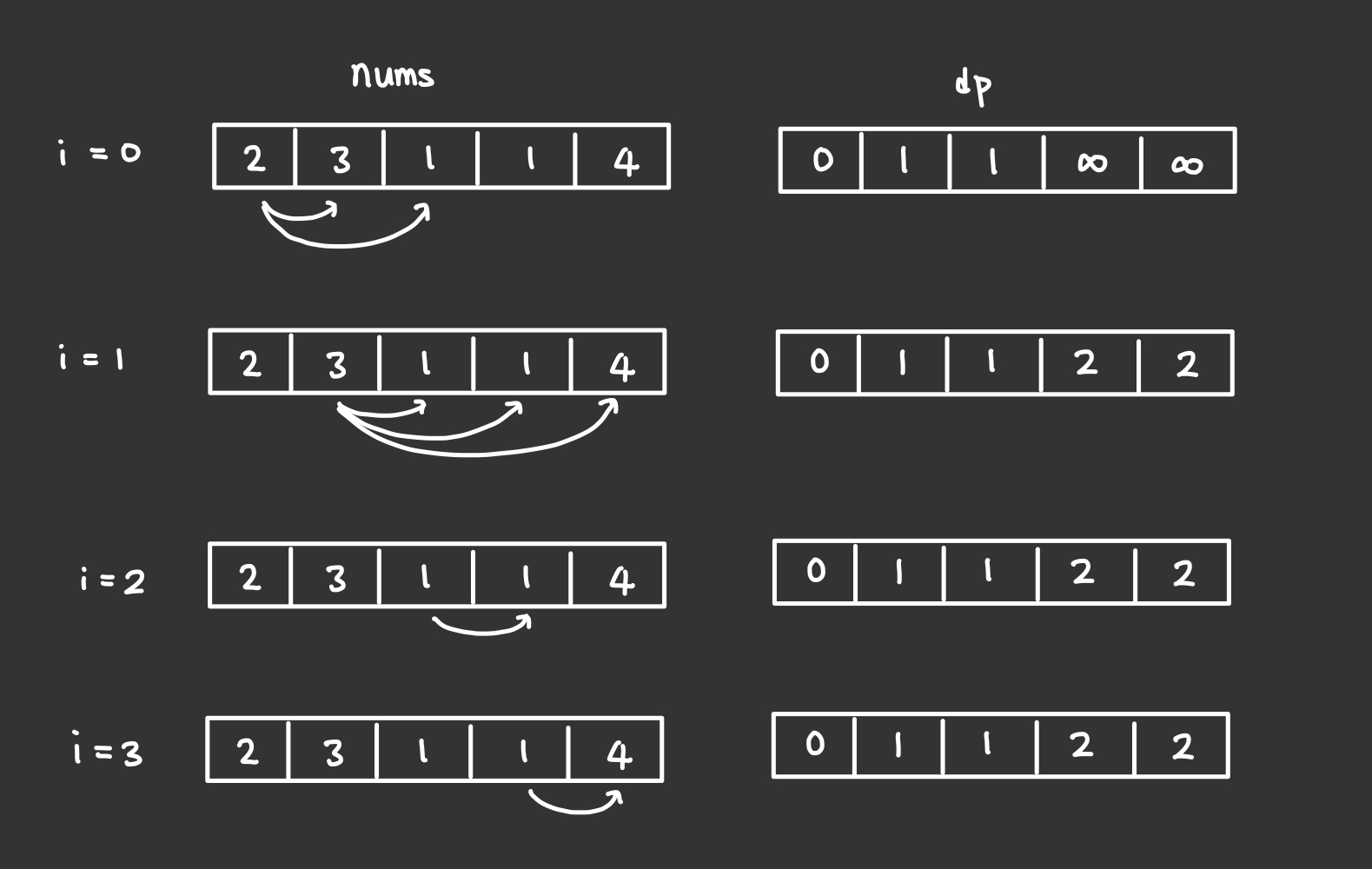
시간복잡도를 계산해보면 O(N^2) 이 된다.
그리고 이전 연산 정보들을 전혀 활용하지 않는 코드이다. 이전의 정보를 활용한다는 것이 무슨 뜻인지 아래 예로 살펴보자.

Prefix를 사용한 풀이 효율성

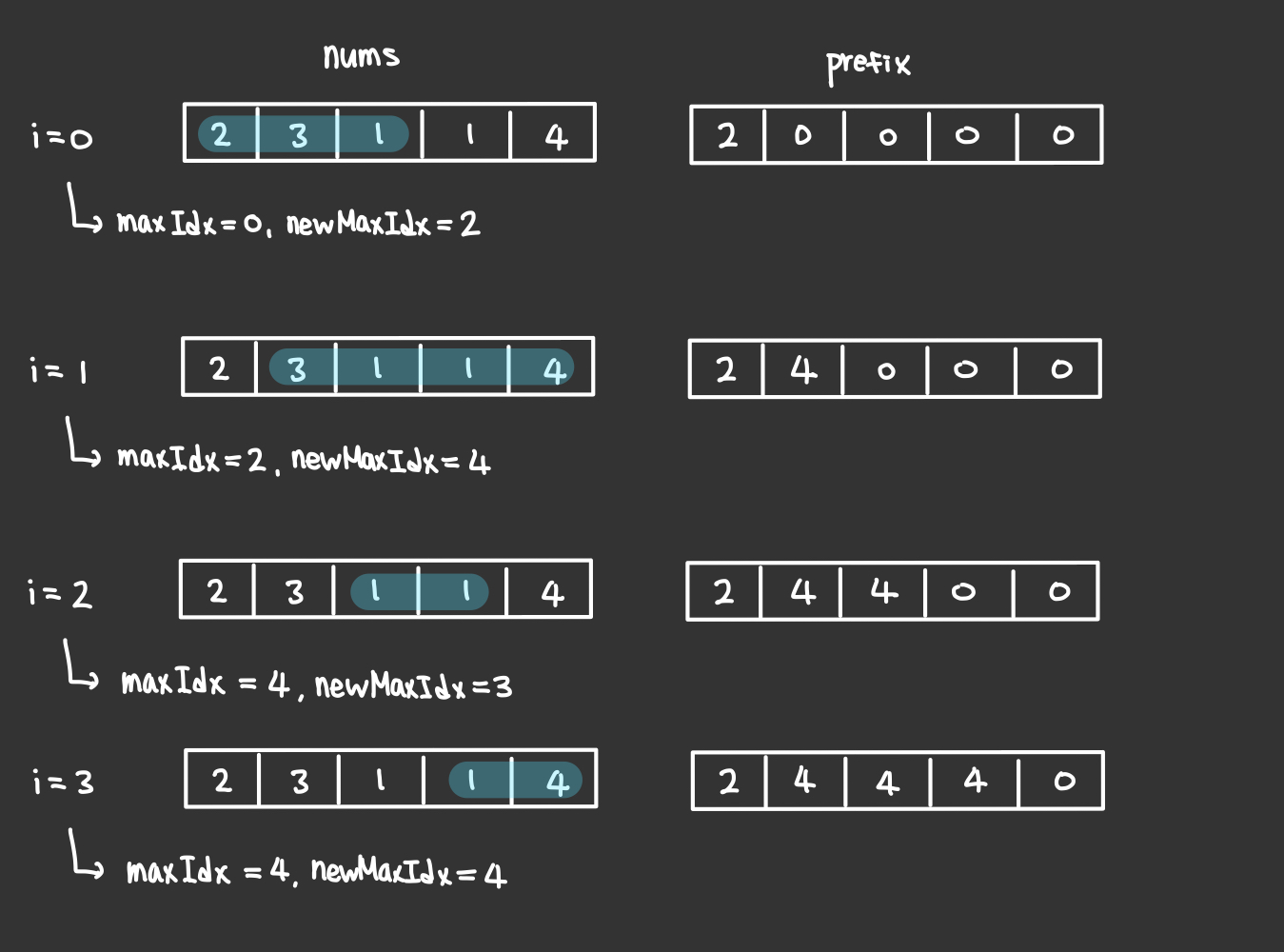
• maxIdx: 현재 도달할 수 있는 최대 idx
• newIdx: 현재 탐색중인 idx에서 도달할 수 있는 최대 idx
• prefix: 해당 idx에서 도달할 수 있는 최대 idx

만약 현재 탐색중인 idx에서

• maxIdx < newMaxIdx
  maxIdx에 newMaxIdx를 저장하고 해당 idx의 prefix에 newMaxIdx를 저장한다.
  
• maxIdx >= newMaxIdx
  해당 idx를 통해 이동하는 것보다 이전 idx를 통해 이동하는 것이 더 멀리 갈 수 있다는 뜻이므로 prefix에 maxIdx를 저장한다.
  

위 방식으로 prefix라는 배열을 완성한 뒤 아래 코드와 같이 순환해주면 이전 연산 결과를 활용해 효율적으로 탐색할 수 있다. 최종적으로 시간복잡도는 O(N)이 된다.

Prefix를 사용한 코드

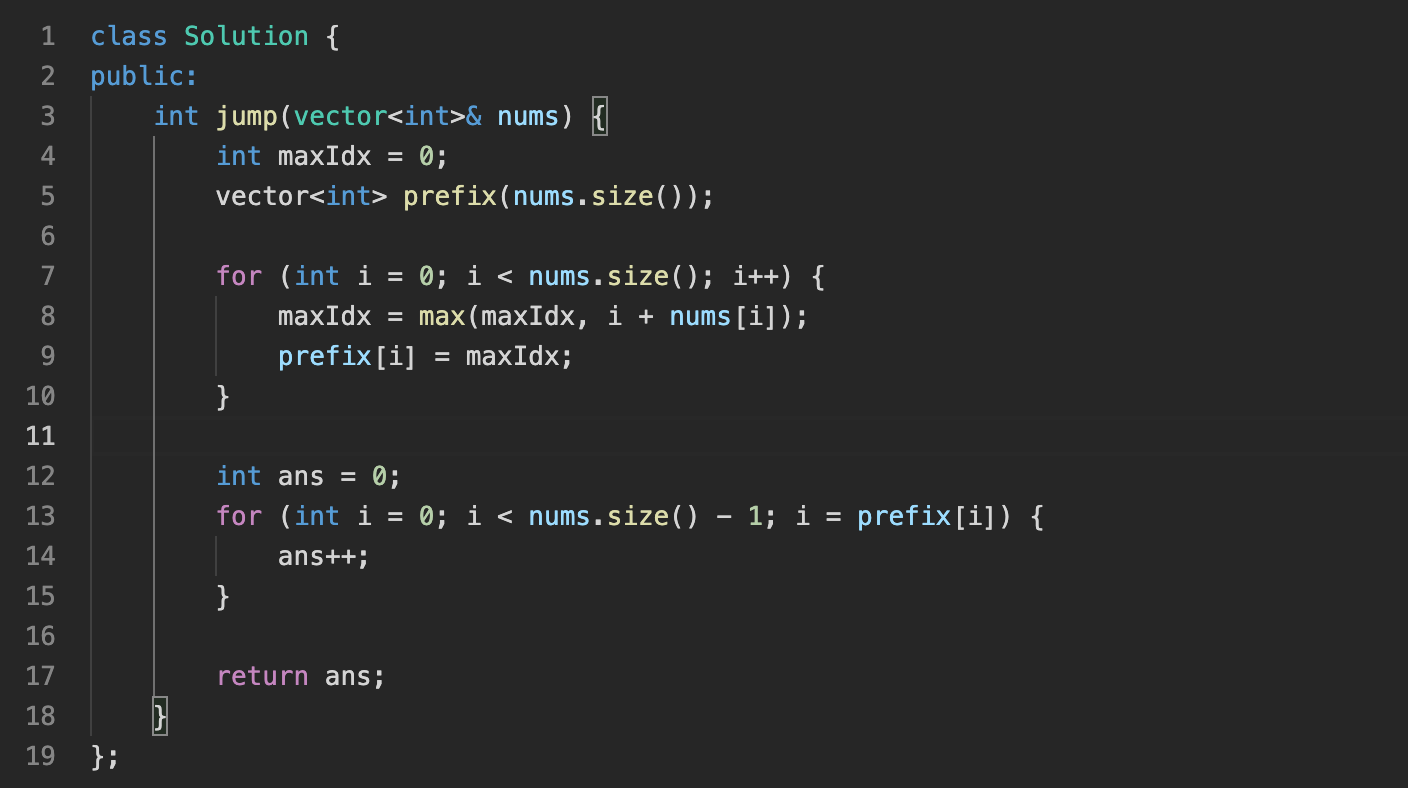
결론

생각해보면 Prefix도 Dynamic Programming이다. Dynamic Programming 자체가 Bottom-Up 접근방식인데 나는 이전 연산을 통해 사용할 수 있는 정보들을 전혀 사용하지 않고 무식하게 모두 탐색했다.
앞으로 코드를 짜기 전에 시간복잡도를 생각하며 더 효율적으로 짜는 방법에 시간 투자를 더 많이 해야겠다.