1. 위상정렬이란?
위키백과에서는 위상정렬을 다음과 같이 정의하고 있다.
유향 그래프의 꼭짓점들(vertex)을 변의 방향을 거스르지 않도록 나열하는 것
즉 Directed Graph에서 Direct를 거스르지 않도록 나열(정렬)하는 것이다. 간단하게 예를 들어보면 다음과 같이 각각의 과목마다 선수과목이 있다고 하자. 
[미적분 -> 공학수학 -> 자료구조] 는 옳은 순서이지만
[알고리즘 -> 자료구조 -> 선형대수학] 은 옳지 않은 순서가 된다.
따라서 우리는 선후 관계가 정의된 그래프 구조 상에서 선후 관계에 따라 정렬하기 위해 위상 정렬을 이용할 수 있다.
cf) 위상정렬을 할 수 없는 경우
- Graph가 Undirected Graph일 때
- Graph가 Cyclic Graph일 때
Graph가 Undirected Graph이면 순서가 정해져 있지 않아 정렬을 하는 의미가 없으므로 위상정렬을 할 수도 할 필요도 없다.
그리고 Graph가 Cyclic Graph일 때 위상정렬을 할 수 없는 이유는 아래에서 아래에서 진입차수와 알고리즘 구현방법에 대해 학습한 후 다시 설명하겠다.
2. 진입차수란?
위상정렬이 무엇이고 어떨 때 쓰이는지는 이제 알았다. 하지만 위상정렬 알고리즘을 구현하려면 '진입차수'라는 개념이 필요하다.
노드 N의 진입차수는 노드 N으로 향하는 간선의 개수이다.
위의 그래프를 예로 들어보자.
선형대수학은 미적분으로부터 엣지가 들어오고 있으므로 진입차수는 1이 된다.
알고리즘은 자료구조와 선형대수학으로부터 엣지가 들어오고 있으므로 진입차수는 2가 된다.
미적분은 들어오는 엣지가 없으므로 진입차수는 0이 된다.
3. 위상정렬 알고리즘 구현
위상정렬은 Kahn 알고리즘과 DFS로 나눌 수 있다. 이번에 다뤄 볼 것은 Kahn 알고리즘이다.
Kahn 알고리즘의 구현방법은 다음과 같다.
Step 1. 진입차수가 0이 된 노드를 Queue에 push한다.
Step 2. Queue를 Pop하고 Answer배열에 추가한다.
Step 2-1. 해당 노드와 연결된 노드의 진입차수를 1 감소시킨다.
이 두가지 step을 Queue가 빌때까지 반복하면 된다.
그래서 Cyclic Graph에서는 왜 못하는 거야?
생각해보자. Cyclic Graph에서는 해당 Cycle의 모든 노드의 진입차수가 0이 아니다. 따라서 진입차수가 절대 0이 되지 않는 구간이 발생하므로 위상정렬이 불가능하다.
4. Kahn 알고리즘 작동 방식
이제 Kahn알고리즘이 실제로 어떻게 작동하는지 예시를 통해 알아보자.

위와 같은 Graph가 있다고 하자.
Queue가 빌 때까지 Step1,Step2를 계속 진행한다.


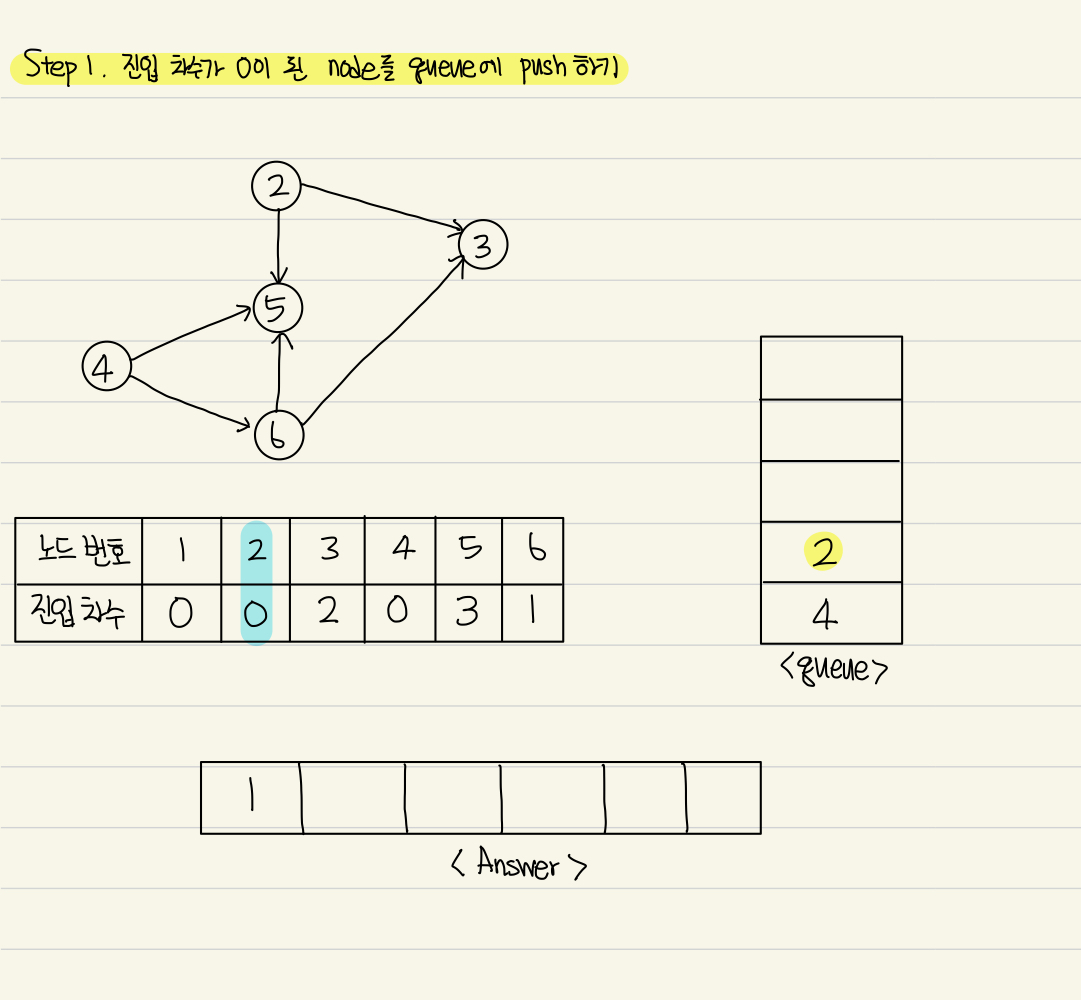

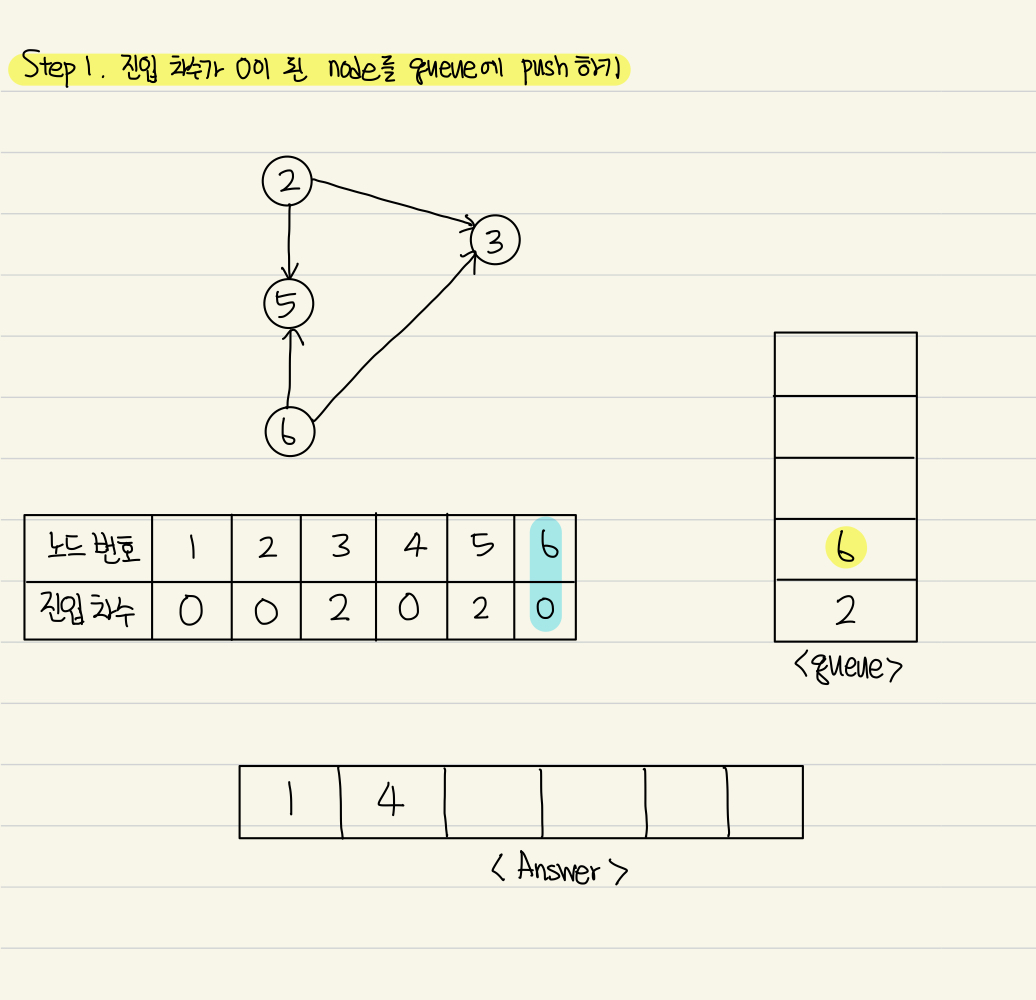




Queue에서 5와 3이 Pop되면서 Queue는 비게 되고 반복이 종료된다.
따라서 Answer의 최종 결과는 1 - 4 - 2 - 6 - 5 - 3이 된다.
5. 코드로 구현 (C++)
vector<int> kahn() { // 위상정렬된 vector를 반환하는 함수
vector<int> answer;
queue<int> q;
for (int i = 1; i <= N; i++) // 모든 노드의 진입차수 계산
for (auto nextNode : adjacent[i])
inDegree[nextNode]++;
for (int i = 1; i <= N; i++) // 진입차수가 0인 노드 queue에 추가
if (inDegree[i] == 0)
q.push(i);
while (!q.empty()) { // queue가 빌 때까지 반복
int curr = q.front();
q.pop();
answer.push_back(curr); // queue에서 pop된 노드 answer에 추가
for (auto n : adjacent[curr]) { // pop된 노드와 인접한 노드의 진입차수 모두 1 감소
inDegree[n]--;
if (inDegree[n] == 0) // 진입차수가 0이 된 노드가 있으면 queue에 추가
q.push(n);
}
}
return answer; // 위상정렬이 완료된 vector 반환
}